Logarithmische Spiralen: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) |
Berny1 (Diskussion | Beiträge) |
||
| Zeile 30: | Zeile 30: | ||
[[Datei:Nautiloids shapes-DE.jpg| miniatur | 400px | Nautilus pompilius]] | [[Datei:Nautiloids shapes-DE.jpg| miniatur | 400px | Nautilus pompilius]] | ||
Das spiralförmige Gehäuse besteht aus verschiedenen Kammern, die jeweils letzte die eigentliche Wohnkammer des Tieres. Ein Gewebestrang, über den Gasaustauch/Wasseraustausch betrieben wird, zieht sich von der Wohnkammer durch die anderen Kammern. Mittels dieses kann der Cephalopode Steigen oder Sinken aber auch rotationsförmige Bewegungen ausführen. Die Scheidewände zwischen den Kammern sind u. a. Unterscheidungsmerkmale einzelner Arten. | Das spiralförmige Gehäuse besteht aus verschiedenen Kammern, die jeweils letzte die eigentliche Wohnkammer des Tieres. Ein Gewebestrang, über den Gasaustauch/Wasseraustausch betrieben wird, zieht sich von der Wohnkammer durch die anderen Kammern. Mittels dieses kann der Cephalopode Steigen oder Sinken aber auch rotationsförmige Bewegungen ausführen. Die Scheidewände zwischen den Kammern sind u. a. Unterscheidungsmerkmale einzelner Arten. | ||
| + | |||
| + | [[Datei:Nautilusk.jpg]]<br> | ||
| + | |||
| + | Das Gehäuse eines Nautilus (ein sogenanntes lebendes Fossil) wird vermessen. Man misst vom Zentrum aus den Winkel und den Radius zum Außenrand der spiralförmigen Windungen. <br> <br> | ||
| + | |||
| + | Die Messergebnisse sind in folgender Tabelle dargestellt:<br> | ||
| + | |||
| + | [[Datei:Logtag1.jpg]] | ||
| + | |||
| + | {{Aufgabe|Weise nach, dass der Radius exponentiell wächst und stelle davon ausgehend | ||
| + | eine Gleichung für den Radius in Abhängigkeit von alpha auf und berechne die fehlenden Radien in | ||
| + | obiger Tabelle. }} | ||
| + | |||
| + | {{Lösung versteckt|}} | ||
| + | |||
| + | {{Aufgabe|Der größte je gefundene „Verwandte“ von Nautilus hatte einen maximalen Radius von ca. 90 cm. | ||
| + | Wieviel Windungen muss das Gehäuse besitzen, wenn es der Gleichung }} | ||
| + | |||
| + | {{Lösung versteckt|}} | ||
| + | Vergleiche nun das Ergebnis mit dem Bild des größten Ammoniten! | ||
| + | {{Aufgabe|Gib zwei Gleichungen an, wie man aus den Angaben für r und alpha die kartesischen Koordinaten | ||
| + | x und y des Punkes P in obiger Skizze berechnen kann. }} | ||
| + | {{Lösung versteckt|}} | ||
Version vom 5. März 2012, 21:58 Uhr
Der Nautilus ist der letzte Repräsentant einer großen Tiergruppe, die seit dem Erdaltertum die Meere der Erde bevölkerte. Zu dieser Tiergruppe gehörten auch die Ammoniten der Jura und Kreidezeit und Ceratiten der Muschelkalkzeit oder wesentlich ältere Goniatiten
Besonders die Gehäuse dieser ektocochleaten (außenhäusige Cephalopoden) Tiere im Gegensatz zu den endocochleaten (innenhäusige Cephalopoden), zu denen die Belemniten der Jurazeit oder die noch heute vertretenen Kalmare, sind faszinierend.
Das spiralförmige Gehäuse besteht aus verschiedenen Kammern, die jeweils letzte die eigentliche Wohnkammer des Tieres. Ein Gewebestrang, über den Gasaustauch/Wasseraustausch betrieben wird, zieht sich von der Wohnkammer durch die anderen Kammern. Mittels dieses kann der Cephalopode Steigen oder Sinken aber auch rotationsförmige Bewegungen ausführen. Die Scheidewände zwischen den Kammern sind u. a. Unterscheidungsmerkmale einzelner Arten.
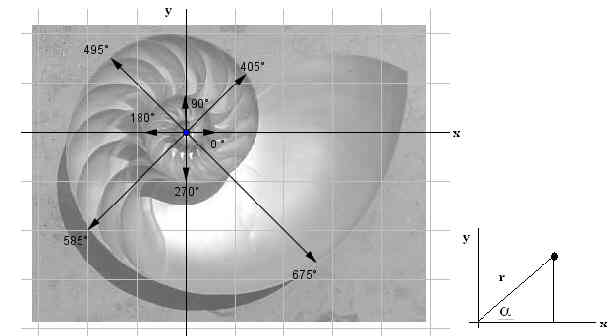
Das Gehäuse eines Nautilus (ein sogenanntes lebendes Fossil) wird vermessen. Man misst vom Zentrum aus den Winkel und den Radius zum Außenrand der spiralförmigen Windungen.
Die Messergebnisse sind in folgender Tabelle dargestellt:
30px Aufgabe
Weise nach, dass der Radius exponentiell wächst und stelle davon ausgehend eine Gleichung für den Radius in Abhängigkeit von alpha auf und berechne die fehlenden Radien in obiger Tabelle. |
30px Aufgabe
Der größte je gefundene „Verwandte“ von Nautilus hatte einen maximalen Radius von ca. 90 cm. Wieviel Windungen muss das Gehäuse besitzen, wenn es der Gleichung |
Vergleiche nun das Ergebnis mit dem Bild des größten Ammoniten!
30px Aufgabe
Gib zwei Gleichungen an, wie man aus den Angaben für r und alpha die kartesischen Koordinaten x und y des Punkes P in obiger Skizze berechnen kann. |