10b 2012-13: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) (→Aufgaben) |
Berny1 (Diskussion | Beiträge) (→Kreis- und Kreisteile - Pi-Bestimmung) |
||
| Zeile 132: | Zeile 132: | ||
{{Aufgabe|* * Fertigen Sie eine vereinfachte Skizze und berechnen Sie in Abhängigkeit vom äußeren und inneren Kreisradius die Länge der Säulen}} | {{Aufgabe|* * Fertigen Sie eine vereinfachte Skizze und berechnen Sie in Abhängigkeit vom äußeren und inneren Kreisradius die Länge der Säulen}} | ||
{{Lösung versteckt|}} | {{Lösung versteckt|}} | ||
| + | == Geometrie am Einheitskreis {von M10} == | ||
| + | |||
| + | |||
| + | '''Das Bogenmaß''' | ||
| + | |||
| + | [http://www.mathe1.de/mathematikbuch/geometrie_bogenmass_126.htm Das Bogenmaß] | ||
| + | |||
| + | [http://www.sengpielaudio.com/Rechner-bogenmass.htm Rechner zum Umrechnen] | ||
| + | |||
| + | '''Polarkoordinaten''' | ||
| + | |||
| + | [http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/rsepp/polarkoord.html Polarkoordinaten und Radar] | ||
| + | |||
| + | '''Trigonometrie am Einheitskreis''' | ||
| + | |||
| + | [http://www.mathematik.net/trigonometrie/tr.htm Arbeitsblätter] - bearbeite in der rechten Spalte "Trigonometrie III" den Abschnitt "Der Einheitskreis". | ||
| + | |||
| + | [http://www.realmath.de/Neues/Klasse10/trigo/eisico.php Sinus- und Kosinuswerte am Einheitskreis] | ||
| + | |||
| + | [http://www.geogebra.org/de/examples/trigo_einheitskreis/einheitskreis1.html Sinus- und Kosinus] | ||
| + | |||
| + | ==Sinus- und Kosinussatz {von M10}== | ||
| + | |||
| + | [[Bild:video2.jpg]] [http://www.youtube.com/watch?v=GdBQzXmuJRg Herleitung des Sinussatzes] und [http://www.youtube.com/watch?v=dCWIuc9toUQ&feature=related Standardaufgabe] | ||
| + | |||
| + | [http://www.geogebra.org/de/upload/files/dynamische_arbeitsblaetter/rsepp/sinussatz.html Der Sinussatz] [http://www.realmath.de/Neues/10zwo/sinsatz/sinussatz.html interaktiv] mit [http://himpsl.htldornbirn.vol.at/mathe_2ai_04_05/24_Sinussatz.doc Berechnungen] | ||
| + | |||
| + | [http://www.realmath.de/Neues/Klasse10/trigo/kosinusflaeche.html Veranschaulichung des Kosinussatzes] | ||
| + | |||
| + | [http://de.wikipedia.org/wiki/Kosinussatz Der Kosinussatz] <br> | ||
| + | [http://www.realmath.de/Neues/10zwo/kosinussatz/kosinussatz.html interaktive Übung]<br> | ||
| + | [http://www.realmath.de/Neues/Klasse10/trigo/kosinusflaeche.html Der Kosinussatz als Verallgemeinerung des Satzes von Pythagoras] | ||
| + | |||
| + | Beispielaufgabe zum [http://www.schule-inside.de/html/m10schoolpage1153.html#1 Sinussatz], [http://www.schule-inside.de/html/m10schoolpage1157.html#1 Kosinussatz] | ||
| + | |||
| + | [http://members.chello.at/gut.jutta.gerhard/kurs/dreiecke.htm Einfache Aufgaben mit Lösungen], [http://wierzioch.com/mathe_uebungen_trigonometrie1/Rm_au040.pdf Aufgaben] | ||
| + | |||
| + | [http://www.mathe-physik-aufgaben.de/mathe_uebungen_trigonometrie1/RM_AU039.pdf Aufgaben] und [http://www.mathe-aufgaben.de/mathecd/16_Trigonometrie/16032%20Trigo%20Training%202%20SODOL.pdf noch mehr Aufgaben] und [http://www.mathe-online.at/mathint/trig/i_aufloesen.html Hinweise] zum Vorgehen. | ||
| + | |||
| + | [http://www.mathepower.com/dreieck.php Berechnungen am allgemeinen Dreieck] | ||
| + | <blockquote></blockquote> | ||
== Grundwissen wiederholen == | == Grundwissen wiederholen == | ||
Version vom 14. November 2012, 12:00 Uhr
Inhaltsverzeichnis |
Mathematik (Heim)
Kreis- und Kreisteile - Pi-Bestimmung
Aufgaben:
|
|
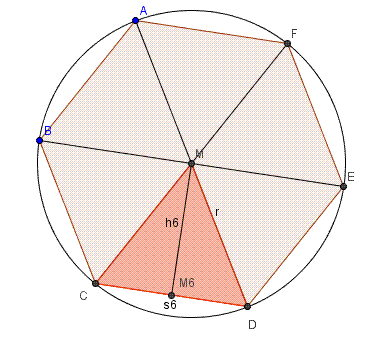
Um die Kreiszahl pi zu bestimmen ist eine Methode einem Kreis reguläre Vielecke ein-/umzubeschreiben wobei mit wachsender Eckenzahl der Umfang des Vielecks gegen den Kreisumfang bzw. die Fläche des Vielecks gegen die Kreisfläche geht im Sinne eines Grenzwertes. Aus dem der Vielecksfläche und dem Quadrat des Radius ergeben sich die (immer genauer werdenden) Näherungswerte für PI. Macht man dies für ein- und umbeschreibene Vielecke, so erhält man eine Intervallschachtelung. |
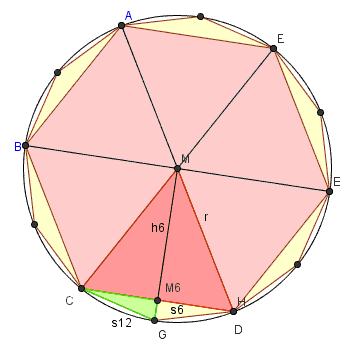
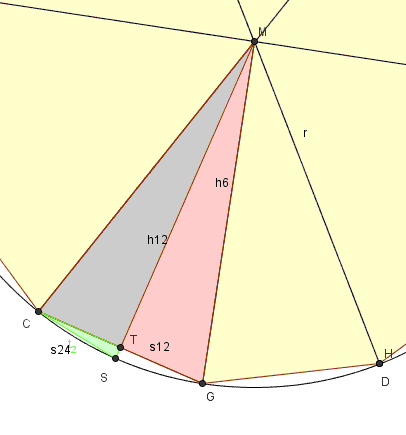
Im folgenden wollen wir ausgehend vom regulären 6-Eck die Flächen des 12-Ecks und des 24-Ecks bestimmen und Näherungswerte für pi berechnen.
|
Lösung:
|
Lösung:
|
Geschichte
Andere Methoden zur Bestimmung der Kreiszahl
Links
Einen ersten Überblick über die Vielfalt der Methoden pi zu bestimmen liefert
Aufgaben
30px Aufgabe
|
Konstruktion:
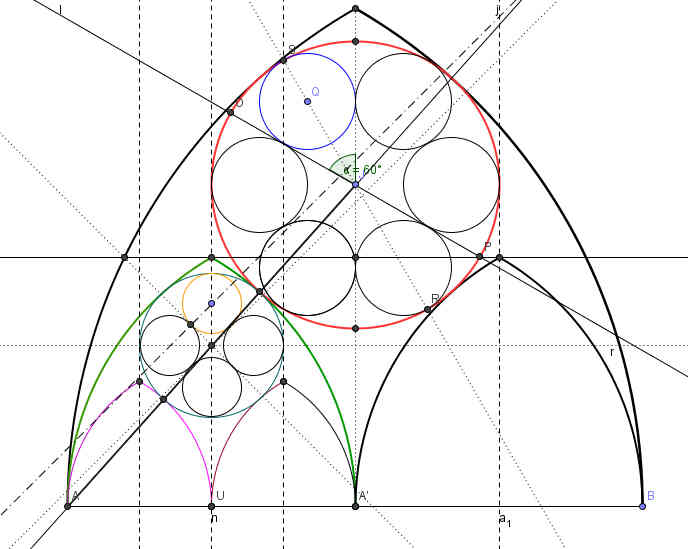
Überlege:
1. Wie groß sind die Radien der inneren gotischen Bögen?
2. Wie groß sind die Radien der Kreise in den Spitzen der gotischen Bögen?
3. Was für Winkel schließen die Tangenten an die Kreise innerhalb der Kreise unter 2 ein?
30px Aufgabe
|
Geometrie am Einheitskreis {von M10}
Das Bogenmaß
Polarkoordinaten
Trigonometrie am Einheitskreis
Arbeitsblätter - bearbeite in der rechten Spalte "Trigonometrie III" den Abschnitt "Der Einheitskreis".
Sinus- und Kosinuswerte am Einheitskreis
Sinus- und Kosinussatz {von M10}
![]() Herleitung des Sinussatzes und Standardaufgabe
Herleitung des Sinussatzes und Standardaufgabe
Der Sinussatz interaktiv mit Berechnungen
Veranschaulichung des Kosinussatzes
Der Kosinussatz
interaktive Übung
Der Kosinussatz als Verallgemeinerung des Satzes von Pythagoras
Beispielaufgabe zum Sinussatz, Kosinussatz
Einfache Aufgaben mit Lösungen, Aufgaben
Aufgaben und noch mehr Aufgaben und Hinweise zum Vorgehen.
Berechnungen am allgemeinen Dreieck
Grundwissen wiederholen
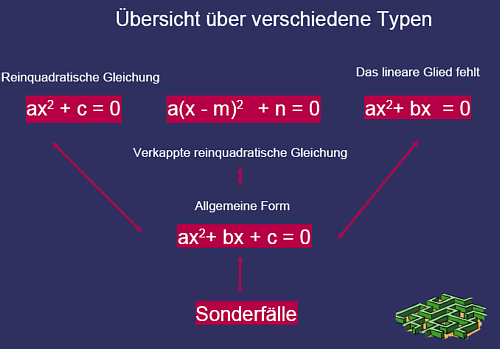
Quadratische Gleichungen - Lösungsstrategien

Geschichte/Sozialkunde (Beck)
- ZDF-Doku zur Kubakrise: Am Rande des Atomkriegs