2013-14 Q11-1M: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) (→{{Schrift grün|Kursthemen}}) |
Berny1 (Diskussion | Beiträge) (→Differenzen- und Differentialquotient) |
||
| Zeile 55: | Zeile 55: | ||
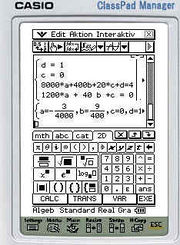
[[Datei: Flasch4.jpg|miniatur||Lösung des Gleichungssystems mit dem Classpad]] | [[Datei: Flasch4.jpg|miniatur||Lösung des Gleichungssystems mit dem Classpad]] | ||
'''2.'''<br> | '''2.'''<br> | ||
| + | |||
| + | |||
| + | |||
Für diese 4 Bedingungen muss man mindestens eine ganzrationale Funktion aufstellen. | Für diese 4 Bedingungen muss man mindestens eine ganzrationale Funktion aufstellen. | ||
| Zeile 85: | Zeile 88: | ||
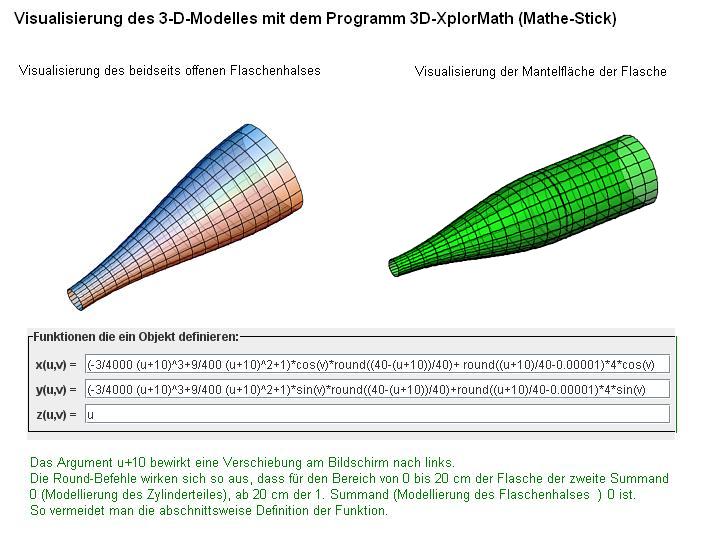
Entnehmen Sie ausgehend von der Höhe von 20 cm der abgebildeten Flasche wesentliche Werte für eine mathematische Modellierung der Flasche. Welchen Grad muss eine ganzrationale Funktion besitzen, um die Flasche als Rotationskörper im Intervall von 0 bis 20] zu erzeugen? Bestimmen Sie diese Funktion.<br> Bestimmen Sie für einen Glasballon, den Sie zuhause besitzen eine erzeugende Funktion und stellen Sie den Glasballon mit dem Ergebnis in einer Präsentation vor. }} | Entnehmen Sie ausgehend von der Höhe von 20 cm der abgebildeten Flasche wesentliche Werte für eine mathematische Modellierung der Flasche. Welchen Grad muss eine ganzrationale Funktion besitzen, um die Flasche als Rotationskörper im Intervall von 0 bis 20] zu erzeugen? Bestimmen Sie diese Funktion.<br> Bestimmen Sie für einen Glasballon, den Sie zuhause besitzen eine erzeugende Funktion und stellen Sie den Glasballon mit dem Ergebnis in einer Präsentation vor. }} | ||
[[File:Glasballon.JPG||400px]] | [[File:Glasballon.JPG||400px]] | ||
| + | |||
| + | ={{Schrift_orange|<big>Koordinatengeometrie</big>}}= | ||
| + | |||
| + | ==Das Skalarprodukt== | ||
| + | |||
| + | Beispiel Skalarprodukt </big> | ||
| + | {{#ev:youtube|Q46b7yQ6o5o|400}} | ||
Aktuelle Version vom 10. Dezember 2013, 10:18 Uhr
Inhaltsverzeichnis |
Lösungen zu Übungsblättern
Übungsblatt Klausurvorbereitung: 
Kursthemen
Diese Mindmap zeigt, was wir in Analysis bisher behandelt haben.
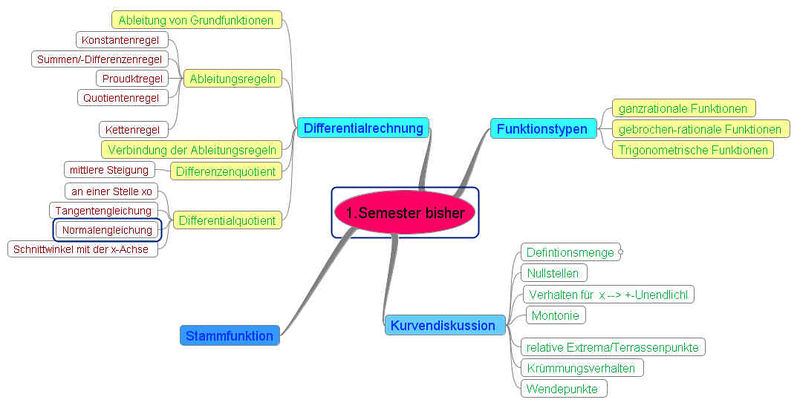
Ausnahme: Krümmungsverhalten und Wendepunkte
In Analysis kommt noch das Newtonsche Nullstellenverfahren hinzu!
Ab Mitte Dezember beginnen wir mit Vektorrechnung!
Gebrochenrationale Funktionen
Wiederholung rationalen Funktionen: rationale Funktionen
Asymptoten bei rationalen Funktionen
Untersuchung von Termen mittels der h-Methode
1. Anwendung: Verhalten an Definitionslücken von gebrochen rationalen Funktionen
2. Im folgenden Kapitel
Differenzen- und Differentialquotient
Anwendungen der Differentialrechnung
Untersuchung von Funktionen auf ihre Eigenschaften
Bestimmung von Funktionen mit bestimmten Eigenschaften!
Aufgabe für die Herbstferien - Vortrag über die Cola-Flasche möglich - melden unter rsg-ws-geo@web.de
30px Aufgabe
 Handelsübliche 1-Liter- Weinflaschen bestehen aus einem zylindrischen Unterteil des Innendurchmessers 8 cm. Der oberste Teil wird durch einen zylindrischen Korken von 2 cm über. Dieser obere nicht zy lindrische Teil geht ist 20 cm hoch. 1. Welche Bedingung muss eine Funktion erfüllen, die die Flasche als Rotationskörper erzeugen soll? |
1.
Bedingungen sind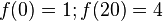 
und wegen des horizontalen Überganges zusätzlich
dass die Ableitung an den Stellen 0 und zwanzig 0 ist.
2.
Für diese 4 Bedingungen muss man mindestens eine ganzrationale Funktion aufstellen.
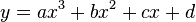mit der Ableitung
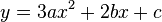
Also ergibt sich das Gleichungssystem
(1)
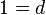
(2)
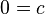
(3)
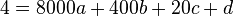
(4)
,
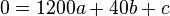
welches durch (1) und (2) auf zwei Gleichungen mit zwei Unbekannten reduziert wird und die
Lösungen
(1)
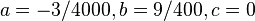und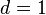 
besitzt.
Ergänzung
Für weitere Untersuchungen:
30px Aufgabe
Entnehmen Sie ausgehend von der Höhe von 20 cm der abgebildeten Flasche wesentliche Werte für eine mathematische Modellierung der Flasche. Welchen Grad muss eine ganzrationale Funktion besitzen, um die Flasche als Rotationskörper im Intervall von 0 bis 20] zu erzeugen? Bestimmen Sie diese Funktion. |
Koordinatengeometrie
Das Skalarprodukt
Beispiel Skalarprodukt </big>
