2015-16-Kurs Heim: Unterschied zwischen den Versionen
Aus RSG-Wiki
Berny1 (Diskussion | Beiträge) |
Berny1 (Diskussion | Beiträge) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | = Binomial verteilung = | |
| + | [[Datei: Weiter.gif]][http://wikis.zum.de/zum/Experimentierkasten_zur_Binomial-_und_Normalverteilung Experimentieren mit den Parametern] | ||
| + | |||
| + | = Bestimmtes Integral - Einführung = | ||
| + | |||
| + | |||
| + | <ggb_applet height="500" width="800" | ||
| + | filename="UntersummeObersumme.ggb" /> | ||
| + | |||
| + | |||
| + | |||
| + | {{Kasten_blau| | ||
| + | |||
| + | [http://de.wikipedia.org/wiki/Formelsammlung_elementare_Algebra#Summenformeln Quelle: Wikipedia] | ||
| + | |||
| + | :<math> \sum_{i=1}^n i = \frac{n(n+1)}{2} </math> (Summe der ersten <math>n</math> ], Der kleine Gauß) | ||
| + | |||
| + | :<math>\sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}</math> (Summe der ersten <math>n</math> ) | ||
| + | |||
| + | :<math>\sum_{i=1}^n i^3 = \left(\frac{n(n+1)}{2}\right)^2 = \frac{n^2(n+1)^2}{4}</math> (Summe der ersten <math>n</math> Kubikzahlen) | ||
| + | |||
| + | :<math>\sum_{i=1}^n i^4 = \frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}</math> (Summe der ersten <math>n</math> Potenzen mit Exponenten 4) | ||
| + | |||
| + | :<math>\sum_{i=1}^n i^5 = \frac {1}{12} n^2 \left(n + 1\right)^2 \left(2n^2 + 2n -1\right)</math> (Summe der ersten <math>n</math> Potenzen mit Exponenten 5) | ||
| + | Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhabersche Formel|Faulhaberschen Formel berechnet werden. | ||
| + | |||
| + | }} | ||
| + | |||
| + | |||
| + | |||
| + | =Integralfunktion= <br><br> | ||
Du kannst den Funktionsterm von f(x), Untergrenze, Obergrenze und a (bis wohin integriert wird) ändern. Angezeigt wird durch die Spur F(x). | Du kannst den Funktionsterm von f(x), Untergrenze, Obergrenze und a (bis wohin integriert wird) ändern. Angezeigt wird durch die Spur F(x). | ||
Aktuelle Version vom 23. November 2015, 10:47 Uhr
Binomial verteilung
Experimentieren mit den Parametern
Bestimmtes Integral - Einführung
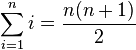(Summe der ersten 
], Der kleine Gauß)
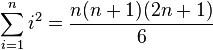(Summe der ersten )
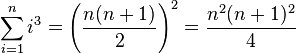(Summe der ersten Kubikzahlen)
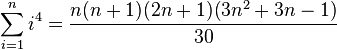(Summe der ersten Potenzen mit Exponenten 4)
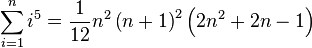(Summe der ersten Potenzen mit Exponenten 5)
Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhabersche Formel
=Integralfunktion=
Du kannst den Funktionsterm von f(x), Untergrenze, Obergrenze und a (bis wohin integriert wird) ändern. Angezeigt wird durch die Spur F(x).
[ tube.geogebra.org is not an authorized iframe site ]
Abituraufgabenbeispiele:
Weitere Materialien: Q 12-Mathematik-Kurs Heim
