10c 2011-12: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „== Kreis- und Kreisteile - Pi-Bestimmung ==“)
 
(→‎Wiederholung wichtiger Grundfunktionen)
 
(28 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
=Mathematik=
 +
== Bayerischer Mathematiktest ==
 +
 +
{|
 +
| Das muss nicht sein. Es gibt auch weitere Möglichkeiten:
 +
 +
 +
 +
* [http://www.isb.bayern.de/isb/index.aspx?MNav=0&QNav=11&TNav=0&INav=0&VTyp=1 Aufgaben und Lösungen der BMTs der letzten Jahre ]
 +
 +
| 
 +
{{#ev:youtube |UK90jf0WsR8|400}}
 +
|}
 +
 +
 
== Kreis- und Kreisteile - Pi-Bestimmung ==
 
== Kreis- und Kreisteile - Pi-Bestimmung ==
 +
<center>
 +
 +
</center>
 +
=== Aufgaben: ===
 +
{|
 +
|
 +
 +
<ggb_applet height="500" width="400" filename="Pi-bestimmung5.ggb" /><br>
 +
| Um die Kreiszahl pi zu bestimmen ist eine Methode einem Kreis reguläre Vielecke ein-/umzubeschreiben wobei mit wachsender Eckenzahl der Umfang des Vielecks gegen den Kreisumfang bzw. die Fläche des Vielecks gegen die Kreisfläche geht im Sinne eines Grenzwertes. Aus dem der Vielecksfläche und dem Quadrat des Radius ergeben sich die (immer genauer werdenden) Näherungswerte für PI.  ''Macht man dies für ein- und umbeschreibene Vielecke, so erhält man eine Intervallschachtelung.''
 +
 +
|}
 +
 +
Im folgenden wollen wir ausgehend vom regulären 6-Eck die Flächen des 12-Ecks und des 24-Ecks bestimmen und Näherungswerte für pi berechnen.
 +
 +
 +
{|
 +
|
 +
 +
[[Datei:Kreis1.GIF]]<br><br>
 +
|
 +
<table cellpadding="2" cellspacing="2" border="0"
 +
style="text-align: left; width: 100%;">
 +
<tr>
 +
<td style="vertical-align: top; background-color: rgb(51, 102, 255); width: 1%;"><br>
 +
</td>
 +
<td style="vertical-align: top;">
 +
'''Arbeitsaufgabe - Gruppenarbeit'''<br>
 +
Berechne die Fläche des regulären 6 - Eckes. '''Tipp:''' Das bestimmende Dreieck ist gleichseitig.Verwende den Satz des Pythagoras 
 +
<br>
 +
<br>
 +
 +
</td>
 +
</tr>
 +
</table>
 +
 +
|}
 +
 +
'''Lösung:'''
 +
:{{Lösung versteckt|
 +
[[Datei:Loeskreis1.gif]]                                   
 +
}}
 +
{|
 +
|
 +
 +
[[Datei:Kreis2.GIF]]<br><br>
 +
|
 +
<table cellpadding="2" cellspacing="2" border="0"
 +
style="text-align: left; width: 100%;">
 +
<tr>
 +
<td style="vertical-align: top; background-color: rgb(51, 102, 255); width: 1%;"><br>
 +
</td>
 +
<td style="vertical-align: top;">
 +
'''Arbeitsaufgabe - Gruppenarbeit'''<br>
 +
Berechne auf gleiche Art die Fläche des regulären 12 - Eckes.
 +
<br>
 +
<br>
 +
 +
</td>
 +
</tr>
 +
</table>
 +
 +
|}
 +
 +
'''Lösung:'''
 +
 +
:{{Lösung versteckt|
 +
[[Datei:Loeskreis2.gif]]                                   
 +
}}
 +
 +
{|
 +
|
 +
 +
[[Datei:Kreis3.GIF]]<br><br>
 +
|
 +
<table cellpadding="2" cellspacing="2" border="0"
 +
style="text-align: left; width: 100%;">
 +
<tr>
 +
<td style="vertical-align: top; background-color: rgb(51, 102, 255); width: 1%;"><br>
 +
</td>
 +
<td style="vertical-align: top;">
 +
'''Arbeitsaufgabe - Gruppenarbeit'''<br>
 +
Berechne auf gleiche Art die Fläche des regulären 24 - Eckes.
 +
<br>
 +
'''Lösung:'''
 +
 +
:{{Lösung versteckt|
 +
[[Datei:Loeskreis3.gif]]                                   
 +
}}
 +
<br>
 +
 +
</td>
 +
</tr>
 +
</table>>
 +
 +
|}
 +
 +
===Geschichte ===
 +
 +
<center>
 +
{{#ev:youtube |FJwzsSPkuWQ|400}}
 +
</center>
 +
 +
===Andere Methoden zur Bestimmung der Kreiszahl ===
 +
<center>{{#ev:youtube |SEaELKaZklM|400}}</center>
 +
 +
===Links===
 +
 +
Einen ersten Überblick über die Vielfalt der Methoden pi zu bestimmen liefert
 +
*[http://de.wikipedia.org/wiki/Kreiszahl#Umbeschreibung_und_Einbeschreibung_bis_zu_96_Ecken]
 +
*sowie [http://www.cwscholz.net/projects/fba/]
 +
 +
== Sinus und Kosinus am Einheitskreis ==
 +
 +
== Sätze am allgemeinen Dreieck  ==
 +
 +
== Sinus- und Kosinusfunktion ==
 +
 +
 +
 +
<table cellpadding="0" cellspacing="0" border="1"
 +
style="text-align: left; width: 100%; background-color: rgb(153, 255, 153);">
 +
<tr style="color: rgb(153, 51, 0);">
 +
<td style="vertical-align: top; background-color: rgb(153, 255, 153); text-align: center;">
 +
 +
== Wiederholung wichtiger Grundfunktionen  == 
 +
</td>
 +
</tr>
 +
<tr>
 +
<td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);">
 +
 +
Diese Zusammenfassung sollst Du Dir ausdrucken:
 +
 +
 +
*[http://www.gymnasium-stein.de/filedownload/Fachschaften/Faecher_Gruppe_2/Mathematik/Downloads/Wichtige_Funktionstypen.pdf Übersicht über Funktionen (zum Ausdruck, vom Gymnasium Stein)]
 +
 +
</td>
 +
</tr>
 +
<tr>
 +
<td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);">
 +
 +
 +
'''Lineare Funktionen''' <br>
 +
 +
[[Bild:lernpfad.jpg]]
 +
*[http://www.matheprisma.de/Module/Geraden/index.htm Geradengleichungen]
 +
*[[Wiederholung lineare Funktionen]]
 +
*Viele ... viele ... Übungen auf der Seinte von [http://www.realmath.de/Mathematik/newmath8.htm realmath.de]
 +
 +
</td>
 +
</tr>
 +
<tr>
 +
<td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);">
 +
 +
'''Quadratische Funktionen''' <br>
 +
 +
 +
 +
[[bild:e-learn.gif]][http://wikis.zum.de/medienvielfalt/index.php/Einf%C3%BChrung_in_quadratische_Funktionen Lernpfad zu quadratischen Funktionen]
 +
 +
'''Parabelgleichungen aufstellen - zuordnen'''
 +
 +
[[Bild:e-learn.gif]][[Bild:ueben.gif]]
 +
*[http://www.zum.de/dwu/umamfu2.htm Lerneinheiten zu Parabeln] (e-Learning)
 +
*[http://brinkmann-du.de/mathe/rbtest/2puzzle/fkt_erkennen_001.htm Lineare und quadratische Funktionen] (interaktiv)
 +
 +
'''Scheitel bestimmen'''
 +
 +
*[http://www.arndt-bruenner.de/mathe/10/scheitelpunkt.htm Scheitel bestimmen - mit Umformungen an beliebiegen quadr. Funktionen]
 +
*[http://www.realmath.de/Neues/Klasse9/parabueb/parabelscheitel.html Interaktive Übung zur Scheitelbestimmung]
 +
 +
'''Anwendungen'''
 +
 +
'''Extremwertaufgaben'''
 +
 +
[[Bild: Ueben.gif]]
 +
*[http://www.physik-im-unterricht.de/emg/G8_Mathe_Klasse_9/M9-Extremwertaufgaben.pdf Extremwertaufgaben zu Parabeln] - mit Lösungen
 +
 +
*eine [http://www.physik-im-unterricht.de/emg/G8_Mathe_Klasse_9/M9-Ex2-03-2008.pdf Stegreifaufgabe zu Extremwerten und Tangenten] an Parabeln mit Lösungen
 +
 +
'''Tangenten an Parabeln'''
 +
 +
*[http://wiki.zum.de/Ber%C3%BChrungsprobleme_bei_quadratischen_Funktionen Sich berührende Graphen]
 +
 +
* [http://www.realmath.de/Neues/Klasse9/tangenten/Tangente.html Tangentengleichung an Parabel bestimmen für ein Geradenbüschel]
 +
 +
*[http://www.dynama.de/dynageo/9/extremwert2/extremwert2.html Graphische Veranschaulichung] (DYNAGEO)
 +
 +
</td>
 +
</tr>
 +
<tr>
 +
<td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);">
 +
 +
'''Funktionen des Typs  a/(x+b) + c (Hyperbeln)'''<br>
 +
 +
*[http://www.matheprisma.uni-wuppertal.de/Module/Hyperbel/index.htm Hyperbeln und rationale Funktionen]
 +
*[[Bild:lernpfad.jpg]] [[rationale Funktionen]]
 +
</td>
 +
</tr>
 +
<tr>
 +
<td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);">
 +
 +
'''Potenzfunktionen'''<br>
 +
</td>
 +
</tr>
 +
<tr>
 +
<td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);">
 +
 +
'''Exponentialfunktionen'''<br>
 +
</td>
 +
</tr>
 +
<tr>
 +
<td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);">
 +
 +
'''Sinus- und Kosinusfunktion''' <br>
 +
</td>
 +
</tr>
 +
</table>
 +
 +
 +
 +
 +
 +
 +
 +
<table cellpadding="0" cellspacing="0" border="1"
 +
style="text-align: left; width: 100%; background-color: rgb(153, 255, 153);">
 +
<tr style="color: rgb(153, 51, 0);">
 +
<td style="vertical-align: top; background-color: rgb(153, 255, 153); text-align: center;">
 +
 +
== Lineares und exponentielles Wachstum  == 
 +
</td>
 +
</tr>
 +
<tr>
 +
<td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);">
 +
 +
{{#ev:youtube |CPo5jjvrf0w|400}}<br>
 +
 +
* Das Bevölkerungsmodell von Thomas Malthus [http://www.geogebra.org/de/examples/malthus/malthus01.htm bei Geogebra]
 +
 +
{{#ev:youtube |7tj-j50Y0es|400}}<br>
 +
 +
*[http://members.chello.at/gut.jutta.gerhard/kurs/exp_wachstum.htm Übungsaufgaben zu exponentiellem Wachstum]
 +
*[http://www.brinkmann-du.de/mathe/gost/efkt_01_02.htm Übungsaufgaben zu exponentiellem Wachstum bzw. Abnahme]
 +
</td>
 +
</tr>
 +
</table>
 +
 +
 +
<table cellpadding="0" cellspacing="0" border="1"
 +
style="text-align: left; width: 100%; background-color: rgb(153, 255, 153);">
 +
<tr style="color: rgb(153, 51, 0);">
 +
<td style="vertical-align: top; background-color: rgb(153, 255, 153); text-align: center;">
 +
 +
== Exponentialgleichungen - Logarithmus ==
 +
</td>
 +
</tr>
 +
<tr>
 +
 +
 +
<td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);"><br>
 +
 +
[[bild: Aktuell.jpg]]<br>
 +
'''Grundlagen:'''
 +
 +
{{#ev:youtube |WBsRWKGd494|400}}<br>
 +
*[http://www.mathematik.net/logarithmen/0-inhalt-1.htm Logarithmische Gesetze] <br>
 +
 +
 +
Logarithmische Umformungen: <br>
 +
 +
'''Übungsaufgaben:''' <br>
 +
[[File:Smarties-UK-Candies.jpg| 150px]]
 +
 +
* [http://www.klassenarbeiten.net/klassenarbeiten/uebungen/klasse10/mathematik/logarithmen/termumformung.shtml Bunte Mischung 1]
 +
* [http://www.brinkmann-du.de/mathe/aufgabenportal/p0_logarithmus_01/p0_logarithmus_01.htm Bunte Mischung 2]
 +
 +
 +
 +
'''Verschiedene Gleichungen:'''
 +
*[http://www.mathe-trainer.de/Klasse10/Exponentialfunktion/Block6/Aufgaben.htm Logarithmuswerte bestimmen]
 +
 +
*[http://www.mathe-trainer.de/Klasse10/Exponentialfunktion/Aufgabensammlung.htm Exponential- und Logarithmische Gleichungen]
 +
*[http://www.mathe-trainer.de/Klasse9/Quadratische_Gleichungen/Aufgabensammlung.htm Quadratische Gleichungen]
 +
 +
 +
[[File:Burgnarren Waldburg 3.jpg| 150px]]<br>
 +
'''Anwendungen:'''
 +
*[http://www.didaktik.mathematik.uni-wuerzburg.de/history/ausstell/rechenschieber/interaktiv.html Interaktiver Rechenschieber]
 +
*[http://www.didaktik.mathematik.uni-wuerzburg.de/history/ausstell/rechenschieber/index.html Alles über den Rechenschieber]
 +
* [[Logarithmische_Spiralen]]Logarithmische Spiralen
 +
</td>
 +
</tr>
 +
</table>

Aktuelle Version vom 16. Oktober 2012, 05:42 Uhr

Inhaltsverzeichnis

Mathematik

Bayerischer Mathematiktest

Das muss nicht sein. Es gibt auch weitere Möglichkeiten:



Kreis- und Kreisteile - Pi-Bestimmung

Aufgaben:


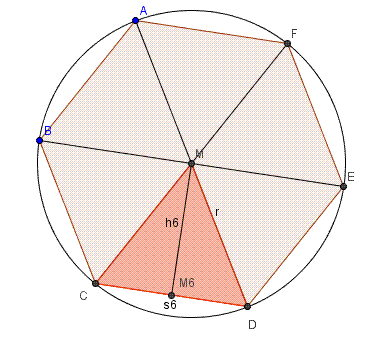
Um die Kreiszahl pi zu bestimmen ist eine Methode einem Kreis reguläre Vielecke ein-/umzubeschreiben wobei mit wachsender Eckenzahl der Umfang des Vielecks gegen den Kreisumfang bzw. die Fläche des Vielecks gegen die Kreisfläche geht im Sinne eines Grenzwertes. Aus dem der Vielecksfläche und dem Quadrat des Radius ergeben sich die (immer genauer werdenden) Näherungswerte für PI. Macht man dies für ein- und umbeschreibene Vielecke, so erhält man eine Intervallschachtelung.

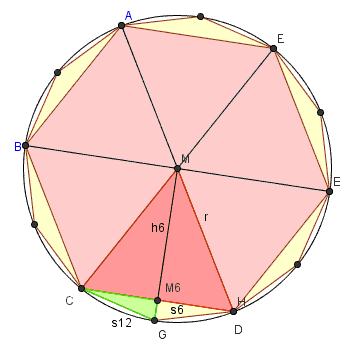
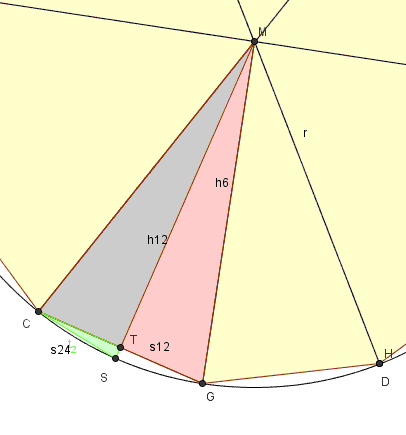
Im folgenden wollen wir ausgehend vom regulären 6-Eck die Flächen des 12-Ecks und des 24-Ecks bestimmen und Näherungswerte für pi berechnen.


Kreis1.GIF

Arbeitsaufgabe - Gruppenarbeit
Berechne die Fläche des regulären 6 - Eckes. Tipp: Das bestimmende Dreieck ist gleichseitig.Verwende den Satz des Pythagoras

Lösung:

Loeskreis1.gif

Kreis2.GIF

Arbeitsaufgabe - Gruppenarbeit
Berechne auf gleiche Art die Fläche des regulären 12 - Eckes.

Lösung:

Loeskreis2.gif

Kreis3.GIF

Arbeitsaufgabe - Gruppenarbeit
Berechne auf gleiche Art die Fläche des regulären 24 - Eckes.
Lösung:

Loeskreis3.gif


>

Geschichte

Andere Methoden zur Bestimmung der Kreiszahl

Links

Einen ersten Überblick über die Vielfalt der Methoden pi zu bestimmen liefert

Sinus und Kosinus am Einheitskreis

Sätze am allgemeinen Dreieck

Sinus- und Kosinusfunktion

Wiederholung wichtiger Grundfunktionen

Diese Zusammenfassung sollst Du Dir ausdrucken:



Lineare Funktionen

Lernpfad.jpg

Quadratische Funktionen


E-learn.gifLernpfad zu quadratischen Funktionen

Parabelgleichungen aufstellen - zuordnen

E-learn.gifUeben.gif

Scheitel bestimmen

Anwendungen

Extremwertaufgaben

Ueben.gif

Tangenten an Parabeln

Funktionen des Typs a/(x+b) + c (Hyperbeln)

Potenzfunktionen

Exponentialfunktionen

Sinus- und Kosinusfunktion




Lineares und exponentielles Wachstum




Exponentialgleichungen - Logarithmus


Aktuell.jpg
Grundlagen:



Logarithmische Umformungen:

Übungsaufgaben:
Smarties-UK-Candies.jpg


Verschiedene Gleichungen:


Burgnarren Waldburg 3.jpg
Anwendungen:

Von „http://rsg.zum.de/index.php?title=10c_2011-12&oldid=3761“