Zauberhafte Mathematik: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) |
Berny1 (Diskussion | Beiträge) |
||
| (15 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
<br><br> | <br><br> | ||
| − | + | ||
<br> | <br> | ||
<br> | <br> | ||
| − | <center>[[datei:Ueg.gif]] </center> | + | <big> |
| + | <big> | ||
| + | <center> | ||
| + | Am Tag der Offenen Tür präsentiert die Fachschaft Mathematik Ihnen und Ihren Kindern: | ||
| + | <br> | ||
| + | </center> | ||
| + | </big> | ||
| + | </big> | ||
| + | <br> | ||
| + | |||
| + | <center>{{#ev:youtube|lHytjEj7B9g|800}}<br><br><br> | ||
| + | [[datei:Ueg.gif]] </center> | ||
<br><br> | <br><br> | ||
| + | </td> | ||
| + | <td style="vertical-align: top; background-color: rgb(255, 2255, 255); text-align: center;"><br> | ||
| + | [[Datei:rsg-logo.gif]] | ||
</td> | </td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
<br> | <br> | ||
| + | |||
| + | ==Armee der Gummibärchen== | ||
| + | [[File:French and German Gummy bears.JPG|200px]]<br> | ||
| + | '''Mit Gummibärchen kann man Mathematik machen!''' <br> | ||
| + | |||
| + | Spielerisch erfahren die Kinder wieviele Möglichkeiten es gibt verschiedenfarbige Gummibärchen oder auch wenn gleichfarbige mit dabei sind nebeneinander auf eine Bank zu setzen. Eine Vorbereitung des Zählprinzips in der Jg. 5 bzw. der Kombinatorik und Wahrscheinlichkeitsrechnung in höheren Jahrgangsstufen. | ||
| + | |||
| + | ==Tal der Schlangen == | ||
| + | |||
| + | [[Datei:Möbiusbd.jpg|400px]]<br> | ||
| + | |||
| + | '''Hier lernen die Kinder ein Papier kennen, das nur eine Seite hat!''' | ||
| + | |||
| + | An diesem Tag sind es nur einfache, aber überraschende Experimente mit Papierschlangen. Letztendlich führen die Betrachtungen an den Experimenten zu Einsichten über endliche, aber unbegrenzte Welten oder gekrümmte „ Räume“ , über zusammenhängende und nichtzusammenhängende Mengen, die Mathematiker, Physiker und Astrophysiker in metaphysischen Überlegungen beschäftigen. | ||
| + | |||
| + | ==Die Ebene der kürzesten Wege== | ||
| + | |||
| + | <center>[[File:Cube Animation.gif]]</center><br> | ||
| + | |||
| + | '''Was ist der kürzeste Weg um von einem Ort zu einem anderen Ort zu kommen?''' | ||
| + | |||
| + | Auf einem Zeichenblatt ist es die geradlinige Verbindung zweier Punkte und es gibt nur eine Lösung. | ||
| + | Schon auf einem Würfel gibt es unter bestimmten Voraussetzungen verschiedene kürzeste Wege um | ||
| + | von einem Punkt zu einem anderen Punkt zu kommen. Lassen Sie sich überrraschen! | ||
| + | ==Insel der verlorenen Hoffnung== | ||
| + | [[Datei:Insel.jpg|400px]][[Datei:Insel1.jpg|400px]]<br><br> | ||
| + | |||
| + | |||
| + | '''Räumliche Vorstellungen trainieren und experimentieren! Auch das ist Mathematik.''' | ||
| + | |||
| + | Puzzles kennt jeder – macht fast jeder gern. Hier können Sie räumliche Puzzles zusammensetzen. | ||
| + | |||
| + | ==Berg der Glückseligkeit== | ||
| + | |||
| + | <center>[[File:Soccer ball.svg|400px]]</center> | ||
| + | |||
| + | |||
| + | <br> | ||
| + | '''Fußball ist für viele ein Sport und eine beliebte Freizeitbeschäftigung.''' | ||
| + | |||
| + | '''Dass der Fußball aber mit Mathematik zu tun hat erfahren Sie hier.''' Der abgebildete Lederfußball ist nämlich ein abgestumpfter Ikosaeder. Das ist einer von insgesamt nur 5 seit der Antike bekannten platonischen Körper. Diese spielten in der griechischen Philosophie, der Mystik des Mittelalters, der Astronomie der frühen Neuzeit aber auch in der Kristallographie eine große Rolle. <br> | ||
| + | [[File:Icosahedron.gif| 150px]][[File:Tetrahedron.gif| 150px]][[File:Dodecahedron.gif| 150px]][[File:120px-Octahedron-slowturn.gif]]<br> | ||
| + | |||
| + | Wer fehlt noch bei den Supermodels der Raumgeometrie?<br> | ||
| + | |||
| + | |||
| + | ==Die Täuschungen der Wüste== | ||
| + | [[File:Mirage 003.jpg|400px]]<br><br> | ||
| + | Eine Fata Morgana! | ||
| + | |||
| + | [[File:Straightlines.svg|400px]]<br><br>[[File:Opt taeuschung groesse.jpg|400px]]<br><br> | ||
| + | [[File:Deutsches Technikmuseum Berlin February 2008 0003.JPG|400px]]<br><br>[[File:Optical illusion.jpg|400px]]<br><br> | ||
| + | |||
| + | '''Warum Mathematiker alles beweisen müssen!''' | ||
| + | |||
| + | Hier erfahren Ihre Kinder, dass sich das Auge leicht täuschen lässt. | ||
| + | |||
| + | ==Im Labyrinth der Dreiecke== | ||
| + | |||
| + | [[Datei:Tdo.jpg]]<br> | ||
| + | |||
| + | |||
| + | '''Der Mathefuchs beweist auf anschauliche Weise den Satz über die Innenwinkelsumme eines Dreiecks.''' | ||
| + | |||
| + | ==Weiterführendes== | ||
| + | |||
| + | {{#ev:youtube |XHS2qVxcDFU|400}} | ||
| + | |||
| + | *Mathematikprofessor Beutelspacher, Begründer des [http://www.mathematikum.de Mathematikums] in Gießen vor Schülern/Ausschnitt aus der Teleakademie des SW-Funks. | ||
| + | [http://www.mathematikum-unterwegs.de/index.php Das Mathematikum unterwegs.] | ||
| + | |||
| + | {{#ev:youtube |uKAIfLA-Zac|400}} | ||
| + | *[http://wikis.zum.de/rsg/Dodekaeder_und_Goldener_Schnitt Goldener Schnitt] | ||
Aktuelle Version vom 7. Februar 2020, 11:10 Uhr
Am Tag der Offenen Tür präsentiert die Fachschaft Mathematik Ihnen und Ihren Kindern:

|
Inhaltsverzeichnis |
Armee der Gummibärchen
200px
Mit Gummibärchen kann man Mathematik machen!
Spielerisch erfahren die Kinder wieviele Möglichkeiten es gibt verschiedenfarbige Gummibärchen oder auch wenn gleichfarbige mit dabei sind nebeneinander auf eine Bank zu setzen. Eine Vorbereitung des Zählprinzips in der Jg. 5 bzw. der Kombinatorik und Wahrscheinlichkeitsrechnung in höheren Jahrgangsstufen.
Tal der Schlangen
Hier lernen die Kinder ein Papier kennen, das nur eine Seite hat!
An diesem Tag sind es nur einfache, aber überraschende Experimente mit Papierschlangen. Letztendlich führen die Betrachtungen an den Experimenten zu Einsichten über endliche, aber unbegrenzte Welten oder gekrümmte „ Räume“ , über zusammenhängende und nichtzusammenhängende Mengen, die Mathematiker, Physiker und Astrophysiker in metaphysischen Überlegungen beschäftigen.
Die Ebene der kürzesten Wege
Was ist der kürzeste Weg um von einem Ort zu einem anderen Ort zu kommen?
Auf einem Zeichenblatt ist es die geradlinige Verbindung zweier Punkte und es gibt nur eine Lösung. Schon auf einem Würfel gibt es unter bestimmten Voraussetzungen verschiedene kürzeste Wege um von einem Punkt zu einem anderen Punkt zu kommen. Lassen Sie sich überrraschen!
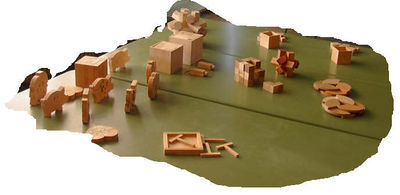
Insel der verlorenen Hoffnung
Räumliche Vorstellungen trainieren und experimentieren! Auch das ist Mathematik.
Puzzles kennt jeder – macht fast jeder gern. Hier können Sie räumliche Puzzles zusammensetzen.
Berg der Glückseligkeit
Fußball ist für viele ein Sport und eine beliebte Freizeitbeschäftigung.
Dass der Fußball aber mit Mathematik zu tun hat erfahren Sie hier. Der abgebildete Lederfußball ist nämlich ein abgestumpfter Ikosaeder. Das ist einer von insgesamt nur 5 seit der Antike bekannten platonischen Körper. Diese spielten in der griechischen Philosophie, der Mystik des Mittelalters, der Astronomie der frühen Neuzeit aber auch in der Kristallographie eine große Rolle.
150px150px150pxDatei:120px-Octahedron-slowturn.gif
Wer fehlt noch bei den Supermodels der Raumgeometrie?
Die Täuschungen der Wüste
400px
Eine Fata Morgana!
Warum Mathematiker alles beweisen müssen!
Hier erfahren Ihre Kinder, dass sich das Auge leicht täuschen lässt.
Im Labyrinth der Dreiecke
Der Mathefuchs beweist auf anschauliche Weise den Satz über die Innenwinkelsumme eines Dreiecks.
Weiterführendes
- Mathematikprofessor Beutelspacher, Begründer des Mathematikums in Gießen vor Schülern/Ausschnitt aus der Teleakademie des SW-Funks.