Q 12-Mathematik-Kurs Heim: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) (→{{Schrift grün|Wahrscheinlichkeitsverteilung, Erwartungswert, Varianz, Standardabweichung}}) |
Berny1 (Diskussion | Beiträge) |
||
| (21 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | {{Aufgaben-blau|1=|2= | |
| + | * Hier könnt Ihr Eure Wünsche für die Karfreitagssitzung formulieren! Am Donnerstag schaue ich mir dann das an! [https://titanpad.com/oJjW8OGFwJ Titanpad] | ||
| + | * Hier [http://www.mathe-aufgaben.com/aufgaben/abitur/bw-allgemein-bildende-gymnasien.html Matheabituraufgaben aus BW] | ||
| + | }} | ||
| − | + | <big><big><big>{{Schrift_orange|Stochastik - Teil 2: Binomialverteilung und ihre Anwendungen in der beurteilenden Statistik}} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | Merkhilfe: in revidierter Form:[http://www.isb.bayern.de/download/11808/merkhilfe_fuer_das_fach_mathematik_standard.pdf] | ||
| + | </big></big></big><br><br><br> | ||
| + | |||
| + | = {{Schrift_grün|Koordinatengeometrie II}} = | ||
| + | |||
| + | == {{Schrift_grün|Geraden im Raum}} == | ||
| + | === Lagebeziehungen von Geraden === | ||
| + | == {{Schrift_grün|Ebenengleichungen}} == | ||
| + | === Punktrichtungsform === | ||
| + | === Normalenform === | ||
| + | === Anwendungen === | ||
| + | ==== Lagebeziehungen von Ebenen ==== | ||
| + | ==== Lagebeziehungen von Gerade und Ebene ==== | ||
| + | ==== Winkel zwischen Ebene un=d Gerade und Ebenen ==== | ||
| + | ==== Winkelhalbierende Ebenen ==== | ||
| + | |||
| + | === Die Hessesche Normalenform === | ||
| + | [[File:Ludwig Otto Hesse.jpg|rechts|200px]] | ||
| + | [http://de.wikipedia.org/wiki/Ludwig_Otto_Hesse Otto Hesse]<br> | ||
| + | [http://de.wikipedia.org/wiki/Hessesche_Normalform Die Hessesche Normalenform]<br> | ||
| + | |||
| + | |||
| + | ==== Anwendungen der Hesseschen Normalenform ==== | ||
| + | ===== Abstände von Punkten und Ebene ===== | ||
| + | ===== Parallelebenen mit bestimmtem Abstand ===== | ||
| + | |||
| + | ={{Schrift grün|Wiederholung von Grundbegriffen}}= | ||
| + | * Experiment <br>{{Lösung versteckt|Versuch, bei dem der Ausgang dem Zufall überlassen ist.}} | ||
| + | * Ergebnis<br> {{Lösung versteckt|Ausgang eines einzelnen Experimentes}} | ||
| + | * Ergebnismenge<br> {{Lösung versteckt|Die Menge mit allen möglichen Ergebnissen des Experimentes}} | ||
| + | * Ereignismenge <br>{{Lösung versteckt|Die Menge aller Teilmengen der Ergebnismenge}} | ||
| + | * Ereignis<br> {{Lösung versteckt|ein Element der Ereignismenge}} | ||
| + | * Laplace-Experiment {{Lösung versteckt|Ein Experiment, bei dem jedes Ergebnis von <math>\Omega</math> gleichwahrscheinlich ist.}} | ||
| + | * Sicheres Ereignis<br> {{Lösung versteckt| hat die Wahrscheinlichkeit 100 %}} | ||
| + | * unmögliches Ereignis <br>{{Lösung versteckt|hat die Wahrscheinlichkeit 0 %}} | ||
| + | * Gegenereignis<br> {{Lösung versteckt|hat die Wahrscheinlichkeit 1 - <math>p(Ereignis)</math>}} | ||
{{Aufgabe|[[Datei:Scheibehmxjkl1!.jpg]]<br> | {{Aufgabe|[[Datei:Scheibehmxjkl1!.jpg]]<br> | ||
| Zeile 15: | Zeile 48: | ||
{{Lösung versteckt|kommt noch}} | {{Lösung versteckt|kommt noch}} | ||
| + | <br> | ||
={{Schrift grün|Wahrscheinlichkeitsverteilung, Erwartungswert, Varianz, Standardabweichung}}= | ={{Schrift grün|Wahrscheinlichkeitsverteilung, Erwartungswert, Varianz, Standardabweichung}}= | ||
| Zeile 38: | Zeile 72: | ||
<br> | <br> | ||
| − | [[Datei:Verteilung2.jpg]] | + | [[Datei:Verteilung2.jpg]][[Datei:Verteilung3.jpg]] |
}} | }} | ||
| Zeile 61: | Zeile 95: | ||
<big><big><big>{{Schrift_orange|Analysis - Teil 2: Integralrechnung und Anwendungen}}</big></big></big> | <big><big><big>{{Schrift_orange|Analysis - Teil 2: Integralrechnung und Anwendungen}}</big></big></big> | ||
| + | |||
| + | ={{Schrift_grün|Signifikanztest}}= | ||
| + | ={{Schrift_grün|Alternativtest}}= | ||
| + | Referat von Julian Kaiser zum Alternativtest | ||
| + | {{#ev:youtube|EkCcs8WAtG4|600}} | ||
| + | = {{Schrift_grün|Ausblick: Normalverteilung}} = | ||
| + | |||
| + | zum Referat von Felix Hörner zwei Videso von Felix Hörner und drei Geogebra-Animationen | ||
| + | |||
| + | {{#ev:youtube|X53uguylvo4|600}}{{#ev:youtube|0S51g0SSlO0|600}} | ||
| + | |||
| + | <ggb_applet height="500" width="1200" | ||
| + | filename="Dichtefunktion1.ggb" /><br><br> | ||
| + | |||
| + | <ggb_applet height="500" width="1200" | ||
| + | filename="Dichtefunktion2auto.ggb" /><br><br> | ||
| + | |||
| + | <ggb_applet height="500" width="1200" | ||
| + | filename="Gaussparam.ggb" /><br><br> | ||
| + | |||
| + | X53uguylvo4& | ||
| + | |||
={{Schrift grün|Krümmungsverhalten und Wendepunkte}}= | ={{Schrift grün|Krümmungsverhalten und Wendepunkte}}= | ||
| Zeile 98: | Zeile 154: | ||
={{Schrift grün|Die Integralfunktion}}= | ={{Schrift grün|Die Integralfunktion}}= | ||
| − | + | [[Veranschaulichung Integralfunktion]] | |
| − | + | ||
| + | |||
| + | |||
| − | |||
| − | |||
{{Aufgabe|Beschreibe wesentliche Eigenschaften der Funktion F(t) für folgende Werte von a:1,2,3,4,-1!<br> | {{Aufgabe|Beschreibe wesentliche Eigenschaften der Funktion F(t) für folgende Werte von a:1,2,3,4,-1!<br> | ||
| Zeile 136: | Zeile 192: | ||
{{Kasten_gelb|[http://www.planet-schule.de/warum/blitze/themenseiten/t4/s1.html Wolkenladung und Blitze]<br> | {{Kasten_gelb|[http://www.planet-schule.de/warum/blitze/themenseiten/t4/s1.html Wolkenladung und Blitze]<br> | ||
[http://de.wikipedia.org/wiki/Elementarladung Elementarladung]}} | [http://de.wikipedia.org/wiki/Elementarladung Elementarladung]}} | ||
| + | |||
| + | |||
| + | Hier entsteht eine weitere anwendungsbezogene Aufgabe: | ||
| + | [[Datei:Deal1.jpg]]<br> | ||
| + | <center>Was ist das?</center><br> | ||
| + | [[Datei:Deal2.jpg]] | ||
| + | {{Lösung versteckt| | ||
| + | '''Freizeitgeographisch''': Ein Lehrer auf Urlaubsfahrt in GB. <br> | ||
| + | '''Naturgeographisch:''' Eine fossile Dünenlandschaft an einer rezenten Sand-Kies-Kliffküste in Deal bei Dover/GB<br> | ||
| + | '''Kulturgeographisch:'''Eine Freizeitanlage, genauer ein englischer Golfplatz<br> | ||
| + | '''Mathematisch:''' Ein Problem der Flächenbestimmung }} | ||
| + | |||
| + | {{Aufgabe| | ||
| + | 1. Schätze die Fläche des Golfplatzes durch elementargeometrische Überlegungen ab.<br> | ||
| + | 2. Modelliere zwei Funktionen f und g, die westlichen und östlichen Begrenzungen des Golfplatzes darstellen können. Hinweis f und g sollen ganzrationale Funktionen möglichst niedrigen Grades sein. Nutze dazu Google-Maps (unten).Drehe dazu das Bild um 90° gegen die Uhrzeigerrichtung.<br> | ||
| + | 3. Bestimme nun mittels Methoden der Analysis die Fläche des Golfplatzes. <br> | ||
| + | 4. Warum ist der unter 3 berechnete Wert nur eine Untergrenze der Fläche des Golfplatzes?}} | ||
| + | |||
| + | <center> | ||
| + | {{#widget:Google Maps | ||
| + | |key=ABQIAAAA2IQiDMxWUKRsL0Y1niI0phTUMGEjHWZULzra_MBruQwfbgZMKBTccWlKGOaga5H4FcqqTXx5ErGNkg | ||
| + | |maptype=satellite | ||
| + | |width=700 | ||
| + | |height=600 | ||
| + | |lat=51.249614 | ||
| + | |lng=1.39595 | ||
| + | |maptypecontrol=yes | ||
| + | |largemapcontrol=yes | ||
| + | |overviewmapcontrol=yes | ||
| + | |scalecontrol=yes | ||
| + | |zoom=14 | ||
| + | |hierarchicalmaptypecontrol=yes | ||
| + | }} | ||
| + | </center> | ||
| + | |||
| + | Hier kommt die Musterlösung hin! | ||
==Kür== | ==Kür== | ||
| Zeile 264: | Zeile 356: | ||
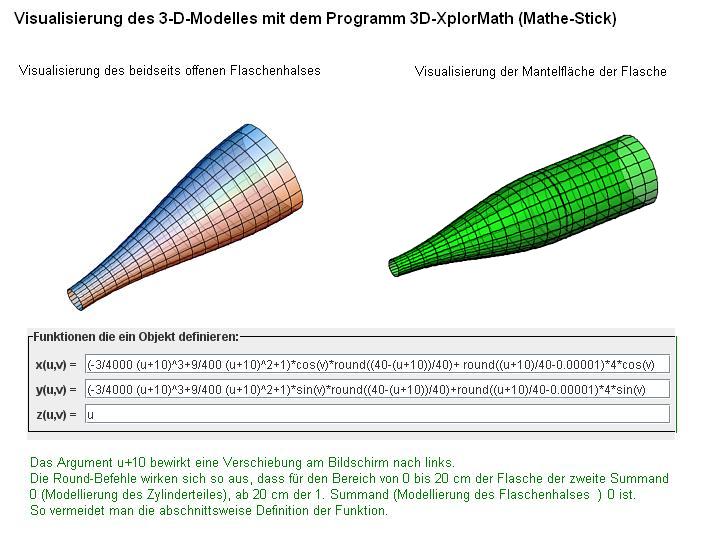
Entnehmen Sie ausgehend von der Höhe von 20 cm der abgebildeten Flasche wesentliche Werte für eine mathematische Modellierung der Flasche. Welchen Grad muss eine ganzrationale Funktion besitzen, um die Flasche als Rotationskörper im Intervall von 0 bis 20] zu erzeugen? Bestimmen Sie diese Funktion.<br> Bestimmen Sie für einen Glasballon, den Sie zuhause besitzen eine erzeugende Funktion und stellen Sie den Glasballon mit dem Ergebnis in einer Präsentation vor. }} | Entnehmen Sie ausgehend von der Höhe von 20 cm der abgebildeten Flasche wesentliche Werte für eine mathematische Modellierung der Flasche. Welchen Grad muss eine ganzrationale Funktion besitzen, um die Flasche als Rotationskörper im Intervall von 0 bis 20] zu erzeugen? Bestimmen Sie diese Funktion.<br> Bestimmen Sie für einen Glasballon, den Sie zuhause besitzen eine erzeugende Funktion und stellen Sie den Glasballon mit dem Ergebnis in einer Präsentation vor. }} | ||
[[File:Glasballon.JPG||400px]] | [[File:Glasballon.JPG||400px]] | ||
| + | |||
| + | = {{Schrift grün|Kursinterne Formelsammlung '''Koordinatengeometrie''' }} = | ||
| + | |||
| + | [http://www.zum.de/Faecher/Ek/BAY/gym/mathematik/kollegstufe/glossargeo/RSG%201M1%20Mathematik%20Heim%202009%2010%20%20K%20o%20o%20r%20d%20i%20n%20a%20t%20e%20n%20g%20e%20o%20m%20e%20t%20r%20i%20e%20%20Kursinterne%20Formelsammlung.htm Formelsammlung Koordinatengeometrie] | ||
= {{Schrift grün|Informationen }} = | = {{Schrift grün|Informationen }} = | ||
| + | |||
| + | |||
| + | == Abiturtraining == | ||
| + | |||
| + | Sehr gutes Material befindet sich unter [http://ne.lo-net2.de/selbstlernmaterial/ Grundwissen, Beispielsaufgaben zu allen Gebieten ] | ||
==Länderübergreifendes Abitur == | ==Länderübergreifendes Abitur == | ||
| + | {{Schrift_grün|Betrifft erst den kommenden Jahrgang}} | ||
[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=22e5bb1a3fd9068cbeb4e5135aa4103a Musteraufgabe mit Zusatzinformationen] | [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=22e5bb1a3fd9068cbeb4e5135aa4103a Musteraufgabe mit Zusatzinformationen] | ||
| + | |||
==CAS-Abitur - traditionelles Abitur== | ==CAS-Abitur - traditionelles Abitur== | ||
[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=86dca814a9e611101a48216c36c37b10 Matheabi]<br>unterscheidet sich nur in Geringfügigkeiten vom <br> | [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=86dca814a9e611101a48216c36c37b10 Matheabi]<br>unterscheidet sich nur in Geringfügigkeiten vom <br> | ||
Aktuelle Version vom 3. April 2015, 04:20 Uhr
Stochastik - Teil 2: Binomialverteilung und ihre Anwendungen in der beurteilenden Statistik
Merkhilfe: in revidierter Form:[1]
Koordinatengeometrie II
Geraden im Raum
Lagebeziehungen von Geraden
Ebenengleichungen
Punktrichtungsform
Normalenform
Anwendungen
Lagebeziehungen von Ebenen
Lagebeziehungen von Gerade und Ebene
Winkel zwischen Ebene un=d Gerade und Ebenen
Winkelhalbierende Ebenen
Die Hessesche Normalenform
Otto Hesse
Die Hessesche Normalenform
Anwendungen der Hesseschen Normalenform
Abstände von Punkten und Ebene
Parallelebenen mit bestimmtem Abstand
Wiederholung von Grundbegriffen
- Experiment
- Ergebnis
- Ergebnismenge
- Ereignismenge
- Ereignis
- Laplace-Experiment
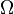 gleichwahrscheinlich ist.
gleichwahrscheinlich ist.- Sicheres Ereignis
- unmögliches Ereignis
- Gegenereignis
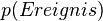
30px Aufgabe
|
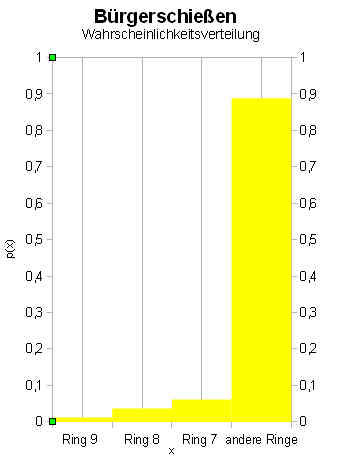
Wahrscheinlichkeitsverteilung, Erwartungswert, Varianz, Standardabweichung
Definition
Ist 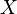 eine Zufallsvariable, die die Werte
eine Zufallsvariable, die die Werte 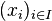 mit den jeweiligen Wahrscheinlichkeiten
mit den jeweiligen Wahrscheinlichkeiten 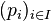 annimmt (mit
annimmt (mit 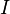 Indexmenge, so errechnet sich der Erwartungswert
Indexmenge, so errechnet sich der Erwartungswert 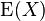 als:
als:
Die Varianz berechnet sich zu:
Die Standardabweichung zu:
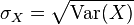
30px Aufgabe
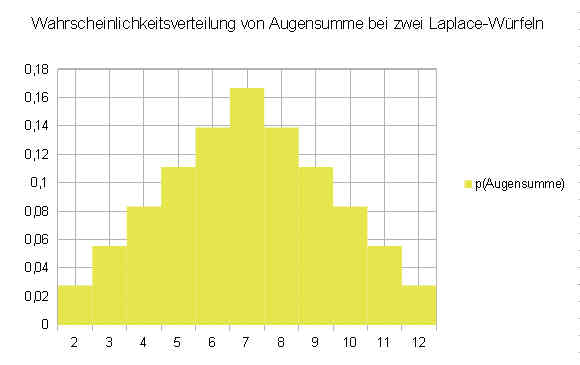
100pxZwei Würfel werden geworfen und die Augensumme gebildet.
|
30px Aufgabe
|
Definition
Ein Glücksspiel heißt fair, wenn der Erwartungswert gleich Null ist.
Bernoulliexperimente und Binomialverteilungen
geplant: Dezember
30px Aufgabe
Folge dem hier angegebenen Link und bearbeite die Aufgaben zur Binomialverteilung! |
Testen von Hypothesen
Analysis - Teil 2: Integralrechnung und Anwendungen
Signifikanztest
Alternativtest
Referat von Julian Kaiser zum Alternativtest
Ausblick: Normalverteilung
zum Referat von Felix Hörner zwei Videso von Felix Hörner und drei Geogebra-Animationen
X53uguylvo4&
Krümmungsverhalten und Wendepunkte
Stammfunktion und Unbestimmtes Integral
Bestimmtes Integral - Einführung
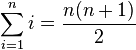 (Summe der ersten
(Summe der ersten  ], Der kleine Gauß)
], Der kleine Gauß)
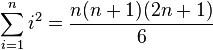 (Summe der ersten
(Summe der ersten  )
)
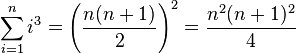 (Summe der ersten
(Summe der ersten  Kubikzahlen)
Kubikzahlen)
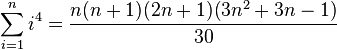 (Summe der ersten
(Summe der ersten  Potenzen mit Exponenten 4)
Potenzen mit Exponenten 4)
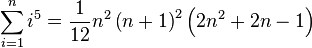 (Summe der ersten
(Summe der ersten  Potenzen mit Exponenten 5)
Potenzen mit Exponenten 5)
Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhabersche Formel
Die Integralfunktion
Veranschaulichung Integralfunktion
30px Aufgabe
Beschreibe wesentliche Eigenschaften der Funktion F(t) für folgende Werte von a:1,2,3,4,-1! |
Zusammenhang zwischen Stammfunktion und bestimmtem Integral - HDI Hauptsatz der Integral und Differentialrechnung
Anwendungen des Bestimmten Integrales - Flächenberechnungen - Weiteres
Pflicht
![]() Einführung in die Integralrechnung
Einführung in die Integralrechnung
Das Riemann-Integral
Überlegungen zur Summenformel
Integral, Fläche, Integralfunktion
Bestimmtes Integral zur Flächenberechnung
Von der Flächen- zur Stammfunktion
![]() Aufgaben zur Integral- und Differentialrechnung
Aufgaben zur Integral- und Differentialrechnung
30px Aufgabe
Delta 12/Seite 59/8-GewitterDatei:Lightning3.jpg Gewitter |
Hier entsteht eine weitere anwendungsbezogene Aufgabe:

Freizeitgeographisch: Ein Lehrer auf Urlaubsfahrt in GB.
Naturgeographisch: Eine fossile Dünenlandschaft an einer rezenten Sand-Kies-Kliffküste in Deal bei Dover/GB
Kulturgeographisch:Eine Freizeitanlage, genauer ein englischer Golfplatz
30px Aufgabe
1. Schätze die Fläche des Golfplatzes durch elementargeometrische Überlegungen ab. |
Hier kommt die Musterlösung hin!
Kür
Zitiert aus Wikipedia:[2]
Berechnung des Volumens eines Rotationskörpers
Rotation um x-Achse
Für einen Rotationskörper, der durch Rotation der Fläche, die durch den Graphen der Funktion f im Intervall [a,b], die x-Achse und die beiden Geraden  und
und 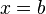 begrenzt wird, um die x-Achse entsteht, lautet die Formel zur Volumenberechnung:
begrenzt wird, um die x-Achse entsteht, lautet die Formel zur Volumenberechnung:
Rotation um y-Achse
Bei Rotation (um die y-Achse) der Fläche, die durch den Graphen der Funktion f im Intervall [a,b], die y-Achse und die beiden Geraden 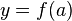 und
und 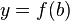 begrenzt wird, muss man
begrenzt wird, muss man 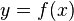 umformen zur Umkehrfunktion
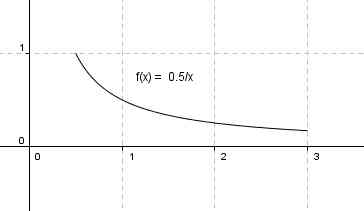
umformen zur Umkehrfunktion 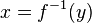 . Diese existiert, wenn f stetig und streng monoton ist. Falls nicht (wie z.B. im Bild rechts oben), lässt sich f vielleicht in Abschnitte zerlegen, in denen f jeweils stetig und streng monoton ist. Die zu diesen Abschnitten gehörenden Volumina müssen dann separat berechnet und addiert werden.
. Diese existiert, wenn f stetig und streng monoton ist. Falls nicht (wie z.B. im Bild rechts oben), lässt sich f vielleicht in Abschnitte zerlegen, in denen f jeweils stetig und streng monoton ist. Die zu diesen Abschnitten gehörenden Volumina müssen dann separat berechnet und addiert werden.
Wenn man hier 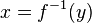 substituiert, erhält man für das Volumen um die y-Achse
substituiert, erhält man für das Volumen um die y-Achse
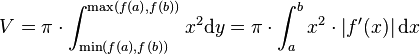 .
.
Der Absolutwert von f' und die min/max Funktionen in den Integralgrenzen sichern ein positives Integral.
Bei Rotation (um die y-Achse) der Fläche, die durch den Graphen der Funktion f im Intervall [a,b], die x-Achse und die beiden Geraden  und
und 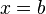 begrenzt wird, gilt die Formel:
begrenzt wird, gilt die Formel:
30px Aufgabe
1. Zeichne einen Halbkreis mit Mittelpunkt (0;0) und Radius r, der eine Funktion darstellt. Gib einen Funktionsterm für die Funktion an und überprüfe die obige Formel durch entsprechende Integration
|
Berechnung der Mantelfläche eines Rotationskörpers
Für die Mantelfläche eines Rotationskörpers gilt:
Rotation um die x-Achse
Herleitung:[3]
30px Aufgabe
Überprüfe die Formel an einem Zylinder bzw. einem Kegel! |
Übungsaufgabe
30px Aufgabe
Datei:GrauburgunderWeinflasche.png handelsübliche Weinflasche - 1 Liter Handelsübliche 1-Liter- Weinflaschen bestehen aus einem zylindrischen Unterteil des Innendurchmessers 8 cm. Der oberste Teil wird durch einen zylindrischen Korken von 2 cm über. Dieser obere nicht zy lindrische Teil geht ist 20 cm hoch. 1. Welche Bedingung muss eine Funktion erfüllen, die die Flasche als Rotationskörper erzeugen soll? 6. Die nebenstehende Abbildung zeigt drei Funktionen t(h), die die Zeit eines Füllvorganges der Flasche mit kegelförmigem Boden in Abhängigkeit von der Füllhöhe h bei konstantem Zufluss (<math<20 cm^3/s, 40 cm^3/s und 80^3 ccm/s)</math> kennzeichnet.(Flasche mit kegelförmigem Boden.
|
1.
Bedingungen sind 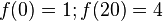 und wegen des horizontalen Überganges zusätzlich
und wegen des horizontalen Überganges zusätzlich
dass die Ableitung an den Stellen 0 und zwanzig 0 ist.
2.
Für diese 4 Bedingungen muss man mindestens eine ganzrationale Funktion aufstellen.
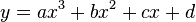 mit der Ableitung
mit der Ableitung
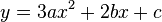
Also ergibt sich das Gleichungssystem
(1)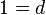
(2)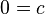
(3)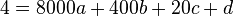
(4)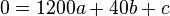
,
welches durch (1) und (2) auf zwei Gleichungen mit zwei Unbekannten reduziert wird und die
Lösungen
(1)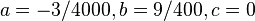 und
und 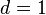 besitzt.
besitzt.
3.
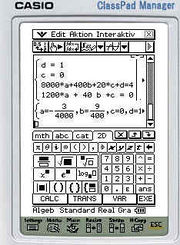
Berechnung des Volumens von Hand und mit CASIO Classpad

4. Das Volumen der Flasche muss 1010 Kubikzentimeter betragen. Mit dem Ergebnis von Aufgabe 3 ergibt sich der Ansatz:
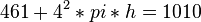 und damit für die Höhe des Zylinders rund 11 cm.
und damit für die Höhe des Zylinders rund 11 cm.
5.
Der Zylinder ist 1 cm zu hoch. Um das Volumen durch die kegelförmige Aussparung im Boden auszugleichen muss der Kegel 3 cm hoch sein, da das Zylindervolumen bei gleichem Grundkreisradius und gleicher Höhe dreimal so groß ist das Kegelvolumen.
6.
Im unteren Bereich der Flasche nimmt die Querschnittsfläche der Flasche mit der Höhe zu. Daher wächst die Zeitdauer(Füllhöhe) überproportional. Darüber wächst im zylinderförmigen Teil die weitere Füllzeit bei gleichem Querschnitt direkt proportional. Im Flaschenhals nimmt dagegen wegen der immer kleiner werdenden Querschnittsfläche die Geschwindigkeit in Abhängigkeit von der Höhe wieder ab.
Zuordnung: 80 - 1 40 - 3 20 - 2
Bis zu einer bestimmten Höhe h hat die Flasche ein festes Volumen! Daher ist bei doppelter Zuflussmenge die halbe Zeit zum Füllen des Volumens notwendig. Also sind die Größen indirekt proportional.
Für weitere Untersuchungen:
30px Aufgabe
Entnehmen Sie ausgehend von der Höhe von 20 cm der abgebildeten Flasche wesentliche Werte für eine mathematische Modellierung der Flasche. Welchen Grad muss eine ganzrationale Funktion besitzen, um die Flasche als Rotationskörper im Intervall von 0 bis 20] zu erzeugen? Bestimmen Sie diese Funktion. |
Kursinterne Formelsammlung Koordinatengeometrie
Formelsammlung Koordinatengeometrie
Informationen
Abiturtraining
Sehr gutes Material befindet sich unter Grundwissen, Beispielsaufgaben zu allen Gebieten
Länderübergreifendes Abitur
Betrifft erst den kommenden Jahrgang Musteraufgabe mit Zusatzinformationen
CAS-Abitur - traditionelles Abitur
Matheabi
unterscheidet sich nur in Geringfügigkeiten vom
CAS-Matheabi
CASIO-Class Pad
Die pdf-Datei kann im Adobe-Reader nach Stichworten durchsucht werden. Also nicht vor der Seitenzahl erschrecken°
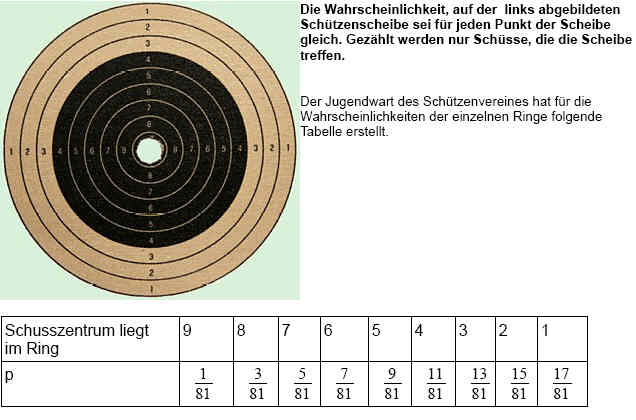

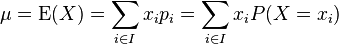
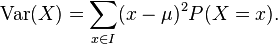
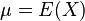 sowie die Varianz als auch die Standardabweichung!
sowie die Varianz als auch die Standardabweichung!
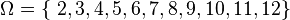




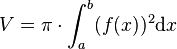
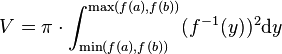
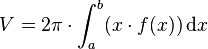
![V = \pi \cdot \int_a^b ( [f(x)]^2\, \mathrm{d}x](/images/math/1/9/f/19f129a01c3584e25247431ed13dd1fb.png) .
.
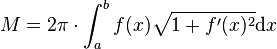
 Platz für Korken und Luft sind?
Platz für Korken und Luft sind?

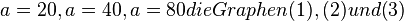 richtig und begründen Sie Ihre Aussage.
richtig und begründen Sie Ihre Aussage.