Logarithmische Spiralen: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) (→Exponentielles Wachstum) |
Berny1 (Diskussion | Beiträge) (→Exponentielles Wachstum) |
||
| Zeile 38: | Zeile 38: | ||
Das spiralförmige Gehäuse besteht aus verschiedenen Kammern, die jeweils letzte die eigentliche Wohnkammer des Tieres. Ein Gewebestrang, über den Gasaustauch/Wasseraustausch betrieben wird, zieht sich von der Wohnkammer durch die anderen Kammern. Mittels dieses kann der Cephalopode Steigen oder Sinken aber auch rotationsförmige Bewegungen ausführen. Die Scheidewände zwischen den Kammern sind u. a. Unterscheidungsmerkmale einzelner Arten. | Das spiralförmige Gehäuse besteht aus verschiedenen Kammern, die jeweils letzte die eigentliche Wohnkammer des Tieres. Ein Gewebestrang, über den Gasaustauch/Wasseraustausch betrieben wird, zieht sich von der Wohnkammer durch die anderen Kammern. Mittels dieses kann der Cephalopode Steigen oder Sinken aber auch rotationsförmige Bewegungen ausführen. Die Scheidewände zwischen den Kammern sind u. a. Unterscheidungsmerkmale einzelner Arten. | ||
| − | + | ---- | |
| − | '''Wiederholung:''' | + | == '''Wiederholung:''' == |
<ggb_applet height="500" width="600" filename="Abhochx.ggb" /><br> | <ggb_applet height="500" width="600" filename="Abhochx.ggb" /><br> | ||
| + | ==Exponentielles Wachstum beim Nautilus == | ||
{{Aufgabe| | {{Aufgabe| | ||
| − | 1. Beschreibe den Einfluss der einzelnen Parameter a, b, c und d. (Probieren | + | 1. Beschreibe den Einfluss der einzelnen Parameter a, b, c und d. (Probieren)<br> |
| − | 2. Warum | + | 2. Warum gilt: Die Basis der Exponentialfunktion muss größer 0 und ungleich 1 sein? (Probieren). Was ergibt sich für ein Funktionentyp für b gleich 1? <br> |
| − | 3. | + | 4. Beschreibe mit Worten am Beispiel eines Graphen, was man unter exponentieller Zunahme/Abnahme versteht bzw. woran man dieses erkennt!Q |
| + | 3. Weitere Grundlagen: [[http://wikis.zum.de/rsg/Grundlegende_Kenntnisse_in_Mathematik#Funktionen]] | ||
}} | }} | ||
{{Lösung versteckt|}} | {{Lösung versteckt|}} | ||
Version vom 5. April 2012, 09:47 Uhr
Mathematik ist das Alphabet, mit dessen Hilfe Gott das Universum beschrieben hat..[Galileo Galilei]
Inhaltsverzeichnis |
Einführung
Der Nautilus ist der letzte Repräsentant einer großen Tiergruppe, die seit dem Erdaltertum die Meere der Erde bevölkerte. Zu dieser Tiergruppe gehörten auch die Ammoniten der Jura und Kreidezeit und Ceratiten der Muschelkalkzeit oder wesentlich ältere Goniatiten
Besonders die Gehäuse dieser ektocochleaten (außenhäusige Cephalopoden) Tiere im Gegensatz zu den endocochleaten (innenhäusige Cephalopoden), zu denen die Belemniten der Jurazeit oder die noch heute vertretenen Kalmare, sind faszinierend.
Das spiralförmige Gehäuse besteht aus verschiedenen Kammern, die jeweils letzte die eigentliche Wohnkammer des Tieres. Ein Gewebestrang, über den Gasaustauch/Wasseraustausch betrieben wird, zieht sich von der Wohnkammer durch die anderen Kammern. Mittels dieses kann der Cephalopode Steigen oder Sinken aber auch rotationsförmige Bewegungen ausführen. Die Scheidewände zwischen den Kammern sind u. a. Unterscheidungsmerkmale einzelner Arten.
Wiederholung:
Exponentielles Wachstum beim Nautilus
30px Aufgabe
1. Beschreibe den Einfluss der einzelnen Parameter a, b, c und d. (Probieren) |
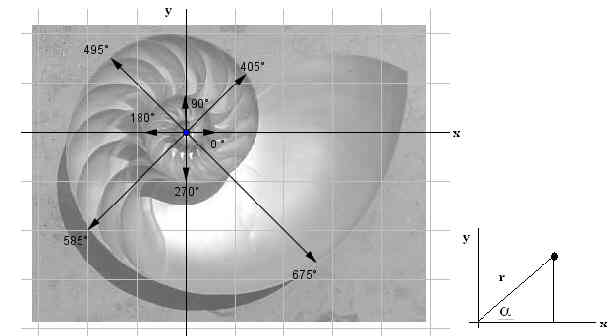
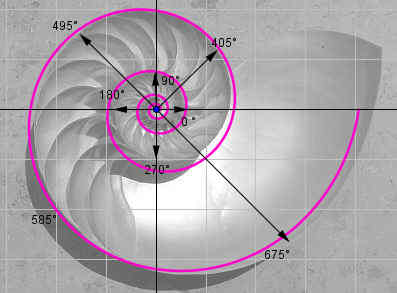
Das Gehäuse eines Nautilus (ein sogenanntes lebendes Fossil) wird vermessen. Man misst vom Zentrum aus den Winkel und den Radius zum Außenrand der spiralförmigen Windungen.
Die Messergebnisse sind in folgender Tabelle dargestellt:
30px Aufgabe
Weise nach, dass der Radius exponentiell wächst und stelle davon ausgehend eine Gleichung für den Radius in Abhängigkeit von alpha auf und berechne die fehlenden Radien in obiger Tabelle. |
30px Aufgabe
Der größte je gefundene „Verwandte“ von Nautilus hatte einen maximalen Radius von ca. 90 cm.
Wieviel Windungen muss das Gehäuse besitzen, wenn es der Gleichung 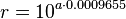
|
Vergleiche nun das Ergebnis mit dem Bild des größten Ammoniten: Fossil des Jahres 2008
30px Aufgabe
Gib zwei Gleichungen an, wie man aus den Angaben für r und alpha die kartesischen Koordinaten x und y des Punkes P in obiger Skizze berechnen kann. |
Das Ergebnis in Geogebra:
Zur Bedeutung der logarithmischen Spirale:
30px Aufgabe
|
Ausblick
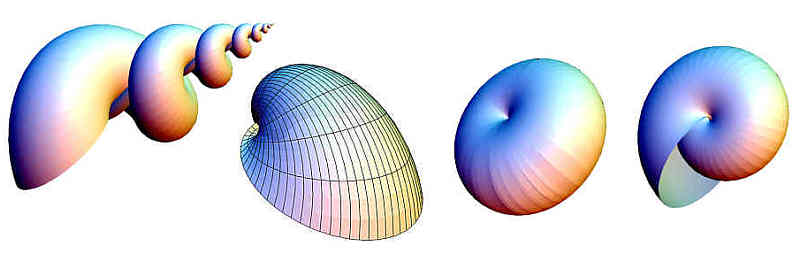
Man kann die Gehäuse vom Nautilus auch in dreidimensionaler Darstellung erzeugen. Eine Vorstellung davon liefert der 3-D-Explorer des Mathe-Sticks unter parametrisierte Kurven.
Durch Veränderung verschiedener Parameter sind aber auch die Schalen anderer Mollusken erzeugbar. Das ist ein Algorithmus, der Einblicke in mögliche Entwicklungen in der Evolution gibt. Dies wurde wohlweislich schon im 19. Jahrhundert erkannt.

- 3D-Explorer Snail-Shell Hier kannst Du selbst experimentieren!
- Virtuelles Museum of Snail Shell
- Ein Video zur kontinuierlichen Deformation räumlicher Molluskengehäuse
Die Logarithmische Spirale in anderen Objekten
30px Aufgabe
1. Untersuche, ob bei den obigen Abbildungen eine logarithmische Spirale vorliegt! |
Weiterführende Betrachtungen - Klasse 11
Kontinuierliches Wachstum - Hinführung zu der Basis e
Betrachtet man beispielsweise die Funktion 2^t, so stellt man fest, dass sich die y-Werte bei Intervallabständen von 1 LE verdoppeln, bei Intervallabständen von 2 LE vervierfachen ... Je nach betrachtetem Intervallabstand beträgt der Wachstumsfaktor 2 bzw. 4 ...
In der Natur läuft Wachstum jedoch nicht in Intervallen, sondern findet kontinuierlich statt und zwar in Abhängigkeit von der Zeit t. Dies kann man durch beliebig kleine Intervalle approximieren. Die Approximation durch n äquidistante Intervalle der Breite (1+1/n)liefert eine Approximation der Funktion 2^t. In der folgenden Geobebradatei kann man diese Approximation simulieren.
30px Aufgabe
Beurteile die Approximation für verschiedene n. Was stellst Du fest? Beobachte auch das Algebrafenster! |
Die Approximation der Funktion ist bei kleiner Anzahl von Intervallen schlecht, bei gößerem n wird die Approximation besser. Einer der Parameter im Algebrafenster nähert sich dem Wert 2,71...
Da in der Natur kontinuerliche Wachstumsvorgänge stattfinden - siehe auch das folgende Kapitel-, die zur Basis e ausgedrückt werden besitzt die Funktion e^t und ihre Umkehrfunktion ln t eine besondere Bedeutung. Die Abkürzung ln kommt vonLogarithmus naturalis.
Betrachtungen zur Frage inwieweit die Infinitesimalrechnung auf zeitliche Vorgänge angewendet werden kann
Die Entdeckung, dass die Objekte in der Natur aus den (ursprünglich) als kleinste Teilchen bezeichneten Atomen besteht und obwohl man in der zwischenzeit einen ganzen "Zoo" von Bausteinen der Atome kennt, glaubt man in der Physik noch immer an "kleinste" Teilchen. Man diskutiert(e) auch, ob die Zeit ein Kontinuum ist oder in kleinsten Einheiten abläuft.
Da wir in der Analysis aber mit Grenzwertprozessen arbeiten und dabei jede noch so kleine vorgegebene Zahl gehen, als beispielsweise bei Längen bzw. Zeiteinheiten, stellt sich die Frage, inwieweit die Infinitesimalrechnung anwendbar ist auf in der Natur ablaufende Prozesse.
Darauf kann und soll hier nur kurz eingegangen Werten:
Innerhalb gewisser Grenzen (Wertebereiche von Längen, Zeit, ...) lassen sich reale Vorgänge hinreichend genau approximieren und mathematisch beschreiben. Für über diesen "makroskopischen Bereich" hinausgehende "mikroskopischen Bereich" braucht man vielleicht andere mathematische Modelle. Ein Beispiel sei die nichteuklidische Geometrie, die für die mathematische Beschreibung in der Relativitätstheorie Einsteins notwendig wurde.
Einige Literaturhinweise :
Neuere Literatur:
Professor Stephen Hawking - Physiker Zur Person Stephen Hawking Stephen Hawings Homapage mit Literatur
Ältere Literatur: - aber lesenswert:
- Barthélemy-Madaule Bergson und Teilhard - Anfänge einer neuen WelterkenntnisZur Person Teilhard de ChardinZur Person Henri Bergson
Fibonacci-Zahlen
Der Goldene Schnitt
![]() Dodekaeder_und_Goldener_Schnitt
Dodekaeder_und_Goldener_Schnitt
Anwendungen der e-Funktion
Liebstöckel
Zur Aufgabe in delta11 S. 154 A 20 Veranschulichung des Wachstums von Pflanzen der maximalen Höhe h= 180 [cm]in Abhängigkeit der Paramer a und k