10c 2011-12: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) (→Lineares und exponentiekkes Wachstum) |
Berny1 (Diskussion | Beiträge) (→Lineares und exponentielles Wachstum) |
||
| Zeile 182: | Zeile 182: | ||
{{#ev:youtube |CPo5jjvrf0w|400}}<br> | {{#ev:youtube |CPo5jjvrf0w|400}}<br> | ||
| + | |||
| + | * Das Bevölkerungsmodell von Thomas Malthus [http://www.geogebra.org/de/examples/malthus/malthus01.htm bei Geogebra] | ||
| + | |||
{{#ev:youtube |7tj-j50Y0es|400}}<br> | {{#ev:youtube |7tj-j50Y0es|400}}<br> | ||
Version vom 26. Februar 2012, 08:22 Uhr
Mathematik
Bayerischer Mathematiktest
| Das muss nicht sein. Es gibt auch weitere Möglichkeiten:
|
Kreis- und Kreisteile - Pi-Bestimmung
Aufgaben:
|
|
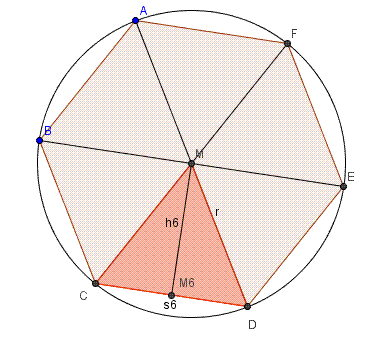
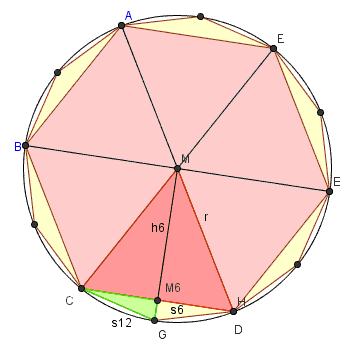
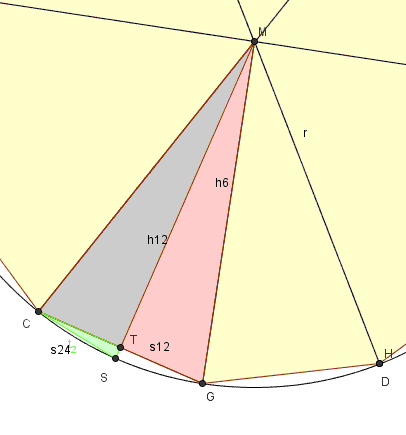
Um die Kreiszahl pi zu bestimmen ist eine Methode einem Kreis reguläre Vielecke ein-/umzubeschreiben wobei mit wachsender Eckenzahl der Umfang des Vielecks gegen den Kreisumfang bzw. die Fläche des Vielecks gegen die Kreisfläche geht im Sinne eines Grenzwertes. Aus dem der Vielecksfläche und dem Quadrat des Radius ergeben sich die (immer genauer werdenden) Näherungswerte für PI. Macht man dies für ein- und umbeschreibene Vielecke, so erhält man eine Intervallschachtelung. |
Im folgenden wollen wir ausgehend vom regulären 6-Eck die Flächen des 12-Ecks und des 24-Ecks bestimmen und Näherungswerte für pi berechnen.
|
Lösung:
|
Lösung:
|
Geschichte
Andere Methoden zur Bestimmung der Kreiszahl
Links
Einen ersten Überblick über die Vielfalt der Methoden pi zu bestimmen liefert
Sinus und Kosinus am Einheitskreis
Sätze am allgemeinen Dreieck
Sinus- und Kosinusfunktion
Wiederholung wichtiger Grundfunktionen |
|
Diese Zusammenfassung sollst Du Dir ausdrucken:
Lineare Funktionen Quadratische Funktionen Funktionen des Typs a/(x+b) + c (Hyperbeln) Sinus- und Kosinusfunktion Potenzfunktion
|
Lineares und exponentielles Wachstum |
|
Exponentialgleichungen - Logarithmus |
Übungsaufgaben:
Verschiedene Gleichungen:
|