Version vom 23. September 2012, 20:01 Uhr

Inhaltsverzeichnis

[Lösung anzeigen][Lösung ausblenden]

Du sollst die Aufgaben zunächst versuchen selbst zu lösen - Bis demnächst

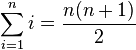$\sum_{i=1}^n i = \frac{n(n+1)}{2}$ (Summe der ersten $n$ ], Der kleine Gauß)

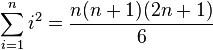$\sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}$ (Summe der ersten $n$ )

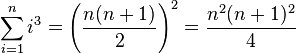$\sum_{i=1}^n i^3 = \left(\frac{n(n+1)}{2}\right)^2 = \frac{n^2(n+1)^2}{4}$ (Summe der ersten $n$ Kubikzahlen)

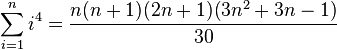$\sum_{i=1}^n i^4 = \frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}$ (Summe der ersten $n$ Potenzen mit Exponenten 4)

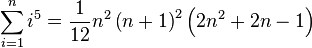$\sum_{i=1}^n i^5 = \frac {1}{12} n^2 \left(n + 1\right)^2 \left(2n^2 + 2n -1\right)$ (Summe der ersten $n$ Potenzen mit Exponenten 5)

Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhabersche Formel

=

@@ Zeile 1: / Zeile 1: @@
-=Stammfunktion und Unbestimmtes Integral=
+=Krümmungsverhalten und Wendepunkte=
+=Stammfunktion und Unbestimmtes Integral=
+[[Datei:Uebintegral12.pdf]]
+{{Lösung versteckt|Du sollst die Aufgaben zunächst versuchen selbst zu lösen - Bis demnächst}}
 =Bestimmtes Integral - Einführung=