10b 2012-13: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) (→{{Schrift grün| Stochastik - Wiederholung von Grundbegriffen}}) |
Berny1 (Diskussion | Beiträge) (→{{Schrift grün| Stochastik - Wiederholung von Grundbegriffen}}) |
||
| Zeile 24: | Zeile 24: | ||
<br> | <br> | ||
| − | {{#ev:youtube|V3jCYm_QGZQ|400}}{{#ev:youtube| | + | {{#ev:youtube|V3jCYm_QGZQ|400}}{{#ev:youtube|u60JF_gBt7A|400}}<br> |
| − | <popup>'''John, Ringo, Georg und Paul''' bedeuteten anfangs der 1960-er Jahre nicht nur eine Revolution in der Musik, sondern waren mit der Anfang eines Wandels in der Nachkriegsgesellschaft. Die vier Pilzköpfe waren für die einen ein Idol, für deren Eltern bedeuteten sie den Untergang des Abendlandes. Die Großmütter waren mit dem Urteil schon etwas vorsichtiger und versuchten ihren Enkeln zu imponieren und die Namen der vier Pilzköpfe den Gesichtern richtig zuzuordnen. | + | {{Aufgabe|1=<popup>'''John, Ringo, Georg und Paul''' bedeuteten anfangs der 1960-er Jahre nicht nur eine Revolution in der Musik, sondern waren mit der Anfang eines Wandels in der Nachkriegsgesellschaft. Die vier Pilzköpfe waren für die einen ein Idol, für deren Eltern bedeuteten sie den Untergang des Abendlandes. Die Großmütter waren mit dem Urteil schon etwas vorsichtiger und versuchten ihren Enkeln zu imponieren und die Namen der vier Pilzköpfe den Gesichtern richtig zuzuordnen. |
| − | a) Wieviele Möglichkeiten gibt es und wie hoch ist die Wahrscheinlichkeit die richtige beim ersten Mal richtig zu haben. | + | a) Wieviele Möglichkeiten gibt es und wie hoch ist die Wahrscheinlichkeit die richtige beim ersten Mal richtig zu haben. <br> |
| − | b) Wie hoch ist die Wahrscheinlichkeit, beim vierten Mal die richtige Zuordnung zu haben. | + | b) Wie hoch ist die Wahrscheinlichkeit, beim vierten Mal die richtige Zuordnung zu haben.<br> |
c) Wie hoch ist die Wahrscheinlichkeit, spätestens beim vierten Mal die richtige Zuordnung zu finden? | c) Wie hoch ist die Wahrscheinlichkeit, spätestens beim vierten Mal die richtige Zuordnung zu finden? | ||
</popup> | </popup> | ||
| + | }} | ||
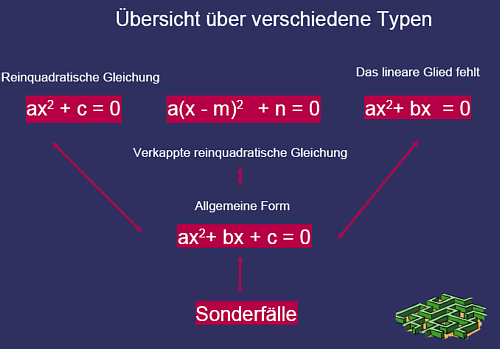
== Kreis- und Kreisteile - Pi-Bestimmung == | == Kreis- und Kreisteile - Pi-Bestimmung == | ||
Version vom 7. Mai 2013, 14:43 Uhr
Inhaltsverzeichnis
|
Mathematik (Heim)
Stochastik - Wiederholung von Grundbegriffen
- Experiment
- Ergebnis
- Ergebnismenge
- Ereignismenge
- Ereignis
- Laplace-Experiment
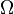gleichwahrscheinlich ist.- Sicheres Ereignis
- unmögliches Ereignis
- Gegenereignis
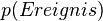
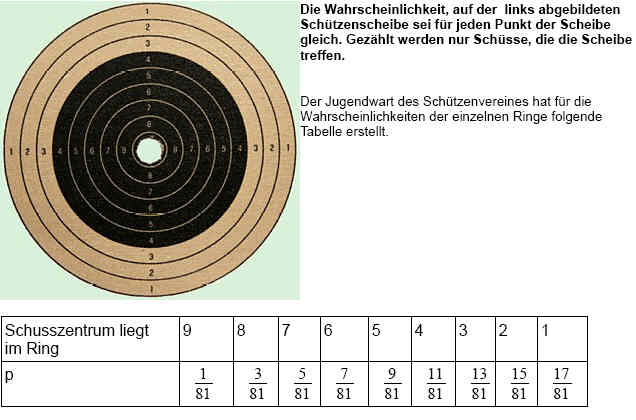
30px Aufgabe
|
30px Aufgabe
|
Kreis- und Kreisteile - Pi-Bestimmung
Aufgaben:
|
|
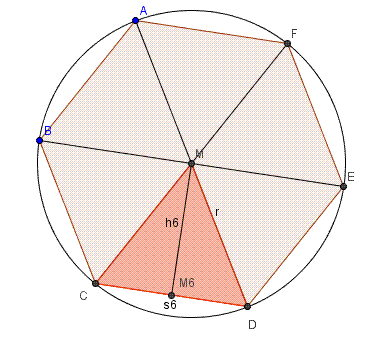
Um die Kreiszahl pi zu bestimmen ist eine Methode einem Kreis reguläre Vielecke ein-/umzubeschreiben wobei mit wachsender Eckenzahl der Umfang des Vielecks gegen den Kreisumfang bzw. die Fläche des Vielecks gegen die Kreisfläche geht im Sinne eines Grenzwertes. Aus dem der Vielecksfläche und dem Quadrat des Radius ergeben sich die (immer genauer werdenden) Näherungswerte für PI. Macht man dies für ein- und umbeschreibene Vielecke, so erhält man eine Intervallschachtelung. |
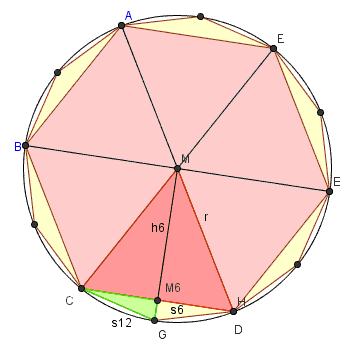
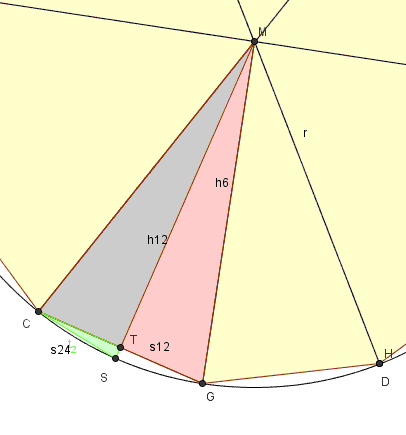
Im folgenden wollen wir ausgehend vom regulären 6-Eck die Flächen des 12-Ecks und des 24-Ecks bestimmen und Näherungswerte für pi berechnen.
|
|
|
Lösung:
|
|
|
Lösung:
|
|
|
Geschichte
Andere Methoden zur Bestimmung der Kreiszahl
Links
Einen ersten Überblick über die Vielfalt der Methoden pi zu bestimmen liefert
Aufgaben
30px Aufgabe
|
Konstruktion:
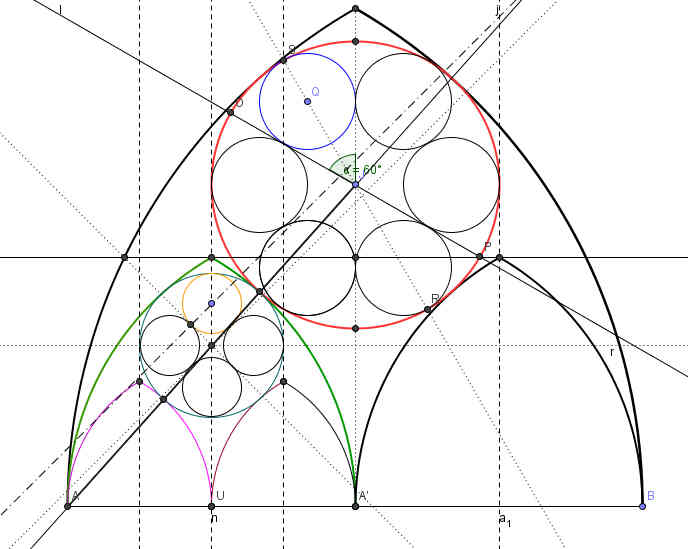
Überlege:
1. Wie groß sind die Radien der inneren gotischen Bögen?
2. Wie groß sind die Radien der Kreise in den Spitzen der gotischen Bögen?
3. Was für Winkel schließen die Tangenten an die Kreise innerhalb der Kreise unter 2 ein?
30px Aufgabe
|
Die Kugel
Aufgaben zum Kugelvolumen und Kugeloberfläche
30px Aufgabe
Überlege Dir sinnvolle Aufgaben zum Berliner Fernsehturm! |
Geometrie am Einheitskreis {von M10}
Das Bogenmaß
Polarkoordinaten
Trigonometrie am Einheitskreis
Arbeitsblätter - bearbeite in der rechten Spalte "Trigonometrie III" den Abschnitt "Der Einheitskreis".
Sinus- und Kosinuswerte am Einheitskreis
Sinus- und Kosinussatz {von M10}
Herleitung des Sinussatzes und Standardaufgabe
Der Sinussatz interaktiv mit Berechnungen
Veranschaulichung des Kosinussatzes
Der Kosinussatz
interaktive Übung
Der Kosinussatz als Verallgemeinerung des Satzes von Pythagoras
Beispielaufgabe zum Sinussatz, Kosinussatz
Einfache Aufgaben mit Lösungen, Aufgaben
Aufgaben und noch mehr Aufgaben und Hinweise zum Vorgehen.
Berechnungen am allgemeinen Dreieck
Sinus- und Kosinusfunktion
Die Sinusfunktion am Einheitskreis
Die allgemeine Sinusfunktion mit Parametern
Lernpfad Trigonometrische Funktionen
Experimentelle Mathematik
Musikalische Graphen
Original und zwei Variationen von Modest Mussorgskys "Bilder einer Ausstellung"
Synthesizer-Variation von TOMITA
Gedanken zur Evolution der Weichtiere
Informationen
Merkhilfe
Die aktualisierte Fassung der Merkhilfe steht auf den Seiten des ISB unter [4] zum Download bereit.
Länderübergreifendes Abitur
Musteraufgabe mit Zusatzinformationen
CAS-Abitur - traditionelles Abitur
Matheabi
unterscheidet sich nur in Geringfügigkeiten vom
CAS-Matheabi
CASIO-Class Pad
Die pdf-Datei kann im Adobe-Reader nach Stichworten durchsucht werden. Also nicht vor der Seitenzahl erschrecken°
- Der Class-Pad im Matheabi von Niedersachsen
- Anwendungsbeispiele
- Arbeitsblätter
- Abeitsblätter von CASIO
Kostenlose Software zum Download CASIO Classpad 330 90-Tage Testversion Download
Grundwissen wiederholen
Kegel, Zylinder, Pyramide - Prinzip von Cavalieri
Quadratische Gleichungen - Lösungsstrategien
Geschichte/Sozialkunde (Beck)
Der Kalte Krieg
- ZDF-Doku zur Kubakrise: Am Rande des Atomkriegs
Videos zum Herbst 1989
- Die Mauer ist offen: kurzes Video mit den wichtigsten Ereignissen des 9.11.1989
- 100 Jahre - "1989 - Das Wunder von Berlin": ZDF Doku (ca. 9 Minuten)
- Ausschnitt aus der Tagesschau vom 10. November 1989
- Szenen aus der Nacht des 9. November 1989: verschiedenen Szenen der jubelnden Menschen
