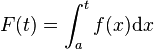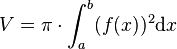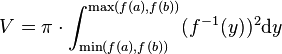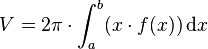Q 12-Mathematik-Kurs Heim
Krümmungsverhalten und Wendepunkte
Stammfunktion und Unbestimmtes Integral
Aufgabe 4:
Da d/dx (ln |f(x)|= f´(x)/f(x)) gilt
- Fehler beim Parsen(Lexikalischer Fehler): V = \int f´(x)/f(x) \mathrm{d}x= ln|f(x)|
. Fällt eine Funktion mit Bruch nicht zerlegbar sein, so prüft man, ob die Voraussetzungen vorliegen oder durch Wahl eines geeigneten Koeffizienten hergestellt werden können. Test:
Aufgabe 5:
Bestimmtes Integral - Einführung
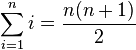 (Summe der ersten
(Summe der ersten  ], Der kleine Gauß)
], Der kleine Gauß)
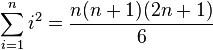 (Summe der ersten
(Summe der ersten  )
)
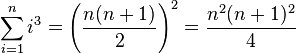 (Summe der ersten
(Summe der ersten  Kubikzahlen)
Kubikzahlen)
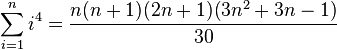 (Summe der ersten
(Summe der ersten  Potenzen mit Exponenten 4)
Potenzen mit Exponenten 4)
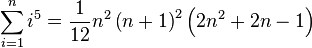 (Summe der ersten
(Summe der ersten  Potenzen mit Exponenten 5)
Potenzen mit Exponenten 5)
Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhabersche Formel
Die Integralfunktion
- Es ist Fehler beim Parsen(Lexikalischer Fehler): f(x) = \0.5 x^2-2
30px Aufgabe
{{{1}}} |
Zusammenhang zwischen Stammfunktion und bestimmtem Integral - HDI Hauptsatz der Integral und Differentialrechnung
Anwendungen des Bestimmten Integrales - Flächenberechnungen - Weiteres
Pflicht
Kür
Zitiert aus Wikipedia:[1]
Berechnung des Volumens eines Rotationskörpers
Rotation um x-Achse
Für einen Rotationskörper, der durch Rotation der Fläche, die durch den Graphen der Funktion f im Intervall [a,b], die x-Achse und die beiden Geraden  und
und 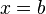 begrenzt wird, um die x-Achse entsteht, lautet die Formel zur Volumenberechnung:
begrenzt wird, um die x-Achse entsteht, lautet die Formel zur Volumenberechnung:
Rotation um y-Achse
Bei Rotation (um die y-Achse) der Fläche, die durch den Graphen der Funktion f im Intervall [a,b], die y-Achse und die beiden Geraden 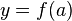 und
und 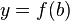 begrenzt wird, muss man
begrenzt wird, muss man 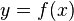 umformen zur Umkehrfunktion
umformen zur Umkehrfunktion 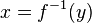 . Diese existiert, wenn f stetig und streng monoton ist. Falls nicht (wie z.B. im Bild rechts oben), lässt sich f vielleicht in Abschnitte zerlegen, in denen f jeweils stetig und streng monoton ist. Die zu diesen Abschnitten gehörenden Volumina müssen dann separat berechnet und addiert werden.
. Diese existiert, wenn f stetig und streng monoton ist. Falls nicht (wie z.B. im Bild rechts oben), lässt sich f vielleicht in Abschnitte zerlegen, in denen f jeweils stetig und streng monoton ist. Die zu diesen Abschnitten gehörenden Volumina müssen dann separat berechnet und addiert werden.
Wenn man hier 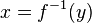 substituiert, erhält man für das Volumen um die y-Achse
substituiert, erhält man für das Volumen um die y-Achse
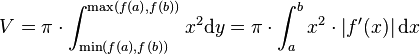 .
.
Der Absolutwert von f' und die min/max Funktionen in den Integralgrenzen sichern ein positives Integral.
Bei Rotation (um die y-Achse) der Fläche, die durch den Graphen der Funktion f im Intervall [a,b], die x-Achse und die beiden Geraden  und
und 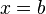 begrenzt wird, gilt die Formel:
begrenzt wird, gilt die Formel:
30px Aufgabe
1. Zeichne einen Halbkreis mit Mittelpunkt (0;0) und Radius r, der eine Funktion darstellt. Gib einen Funktionsterm für die Funktion an und überprüfe die obige Formel durch entsprechende Integration 3. |
Informationen
Länderübergreifendes Abitur
Musteraufgabe mit Zusatzinformationen
CAS-Abitur - traditionelles Abitur
Matheabi
unterscheidet sich nur in Geringfügigkeiten vom
CAS-Matheabi
CASIO-Class Pad
Die pdf-Datei kann im Adobe-Reader nach Stichworten durchsucht werden. Also nicht vor der Seitenzahl erschrecken°