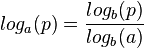M10 Der Logarithmus
Die Gleichung 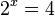 ist ganz leicht zu lösen. Man erhält
ist ganz leicht zu lösen. Man erhält 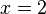 . Dies geht immer gut, wenn der Wert auf der rechten Seite eine Potenz der Basis ist, also
. Dies geht immer gut, wenn der Wert auf der rechten Seite eine Potenz der Basis ist, also
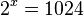 hat die Lösung
hat die Lösung 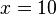 ,
,
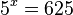 hat die Lösung
hat die Lösung 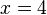 ,
,
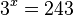 hat die Lösung
hat die Lösung 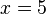 .
.
Doch was macht man, wenn die Gleichung 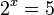 lautet?
lautet?
Man hatte schon einmal ein ähnliches Problem. Die Gleichung 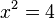 hat die Lösungen
hat die Lösungen 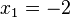 und
und 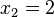 . Für die Gleichung
. Für die Gleichung 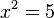 hat man dann neue Zahlen eingeführt, die Wurzeln, und die Gleichung hatte die Lösungen
hat man dann neue Zahlen eingeführt, die Wurzeln, und die Gleichung hatte die Lösungen 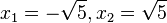 .
.
Für die Gleichung 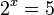 muss man, um eine Lösung zu haben, neue Zahlen einführen, die Logarithmen bzw. den Logarithmus.
muss man, um eine Lösung zu haben, neue Zahlen einführen, die Logarithmen bzw. den Logarithmus.
|
Merke:
Die Gleichung Man spricht für  |
Beispiele: 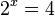 hat die Lösung
hat die Lösung 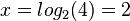
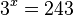 hat die Lösung
hat die Lösung 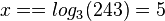
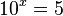 hat die Lösung
hat die Lösung 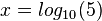
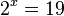 hat die Lösung
hat die Lösung 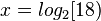
1a) 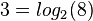
b) 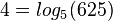
c) 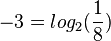
d) 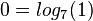
e) 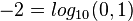
f) 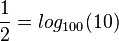
2a) 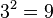
b) 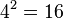
c) 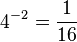
d) 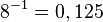
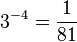
|
Merke:
Es ist
|
Stelle eventuell die passende Exponentialgleichung auf!
Für log2(32) lautet die Exponentialgleichung 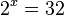 , also x = 5
, also x = 5
1a) 5; b) 10; c) 5; d) 1; e) 4; f) 0; g) -1; h) -3; i) -2; k) -1; l) -2; m) -3
n) -1; o) -1; p) -3; q) 2; r) 0; s) 2; t) 1; u) -1; v) 2; w) 0; x) -1; y) -2
2a) 0,5; b) 0,5; c)  ; d)
; d)  ; e)
; e)  ; f)
; f)  ; g)
; g)  ; h) 5;
; h) 5;
 ; k) 0,5; l)
; k) 0,5; l)  ; m)
; m) 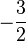 ; o) 2; p) -2; q) 0
; o) 2; p) -2; q) 0
|
Merke:
Rechengesetze des Logarithmus Logarithmus eines Produkts: Logarithmus eines Quotienten: Logarithmus einer Potenz: |
Zur Begründung der Rechenregeln:
1. 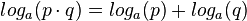 erhält man durch folgende Überlegung:
erhält man durch folgende Überlegung:
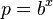 und
und 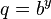 . Dann ist
. Dann ist 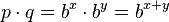 , also
, also 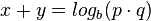 .
.
Da 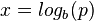 und
und 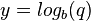 ist erhält man
ist erhält man 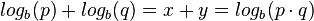 .
.
2. 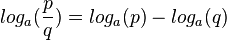 erhält man durch folgende Überlegung:
erhält man durch folgende Überlegung:
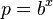 und
und 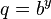 . Dann ist
. Dann ist 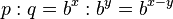 , also
, also 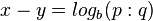 .
.
Da 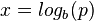 und
und 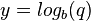 ist erhält man
ist erhält man 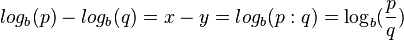 .
.
Beispiele:1. 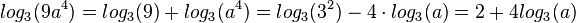
2. ![log_{10}(1000\cdot\sqrt[5]{a^2}=log_{10}(1000)+log_{10}(a^{\frac{2}{5}})=3 +\frac{2}{5}log_{10}(a)](/images/math/b/0/4/b04b343917aa8efa40b64fd674cc11fb.png)
3. 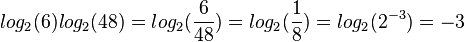
30px Merke
Für Für Diese beiden Symbole findest du auch auf dem Taschenrechner. |
4. 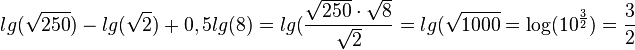
|
Merke:
Basiswechsel: |

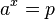 mit a
mit a 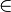 R+ und p > 0 hat die Lösung
R+ und p > 0 hat die Lösung 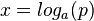 .
.
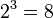
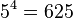
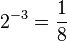 d)
d) 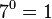
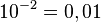
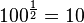
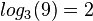
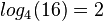
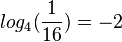
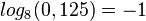
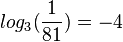
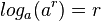
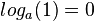
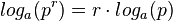
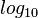 schreibt man
schreibt man 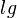
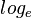 schreibt man
schreibt man 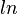 , wenn e die Eulersche Zahl e = 2, 718 281 828 459 045 235 360 287 ... ist.
, wenn e die Eulersche Zahl e = 2, 718 281 828 459 045 235 360 287 ... ist.