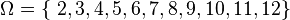Q 12-Mathematik-Kurs Heim
Stochastik - Teil 2: Binomialverteilung und ihre Anwendungen in der beurteilenden Statistik
Merkhilfe: in revidierter Form:[1]
Koordinatengeometrie II
Geraden im Raum
Lagebeziehungen von Geraden
Ebenengleichungen
Punktrichtungsform
Normalenform
Anwendungen
Lagebeziehungen von Ebenen
Lagebeziehungen von Gerade und Ebene
Winkel zwischen Ebene un=d Gerade und Ebenen
Winkelhalbierende Ebenen
Die Hessesche Normalenform
Otto Hesse
Die Hessesche Normalenform
Anwendungen der Hesseschen Normalenform
Abstände von Punkten und Ebene
Parallelebenen mit bestimmtem Abstand
Wiederholung von Grundbegriffen
- Experiment
- Ergebnis
- Ergebnismenge
- Ereignismenge
- Ereignis
- Laplace-Experiment
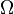 gleichwahrscheinlich ist.
gleichwahrscheinlich ist.- Sicheres Ereignis
- unmögliches Ereignis
- Gegenereignis
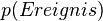
30px Aufgabe
|
Wahrscheinlichkeitsverteilung, Erwartungswert, Varianz, Standardabweichung
Definition
Ist 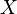 eine Zufallsvariable, die die Werte
eine Zufallsvariable, die die Werte 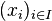 mit den jeweiligen Wahrscheinlichkeiten
mit den jeweiligen Wahrscheinlichkeiten 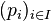 annimmt (mit
annimmt (mit 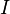 Indexmenge, so errechnet sich der Erwartungswert
Indexmenge, so errechnet sich der Erwartungswert 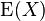 als:
als:
Die Varianz berechnet sich zu:
Die Standardabweichung zu:
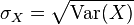
30px Aufgabe
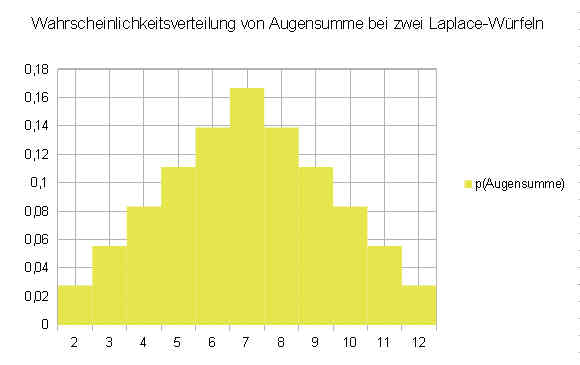
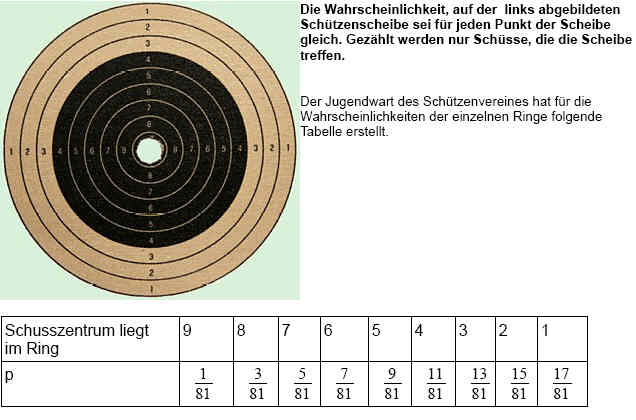
100pxZwei Würfel werden geworfen und die Augensumme gebildet.
|
30px Aufgabe
|
Definition
Ein Glücksspiel heißt fair, wenn der Erwartungswert gleich Null ist.
Bernoulliexperimente und Binomialverteilungen
geplant: Dezember
30px Aufgabe
Folge dem hier angegebenen Link und bearbeite die Aufgaben zur Binomialverteilung! |
Testen von Hypothesen
Analysis - Teil 2: Integralrechnung und Anwendungen
Signifikanztest
Alternativtest
Referat von Julian Kaiser zum Alternativtest
Ausblick: Normalverteilung
zum Referat von Felix Hörner zwei Videso von Felix Hörner und drei Geogebra-Animationen
X53uguylvo4&
Krümmungsverhalten und Wendepunkte
Stammfunktion und Unbestimmtes Integral
Bestimmtes Integral - Einführung
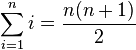 (Summe der ersten
(Summe der ersten  ], Der kleine Gauß)
], Der kleine Gauß)
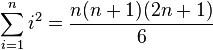 (Summe der ersten
(Summe der ersten  )
)
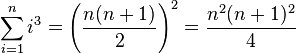 (Summe der ersten
(Summe der ersten  Kubikzahlen)
Kubikzahlen)
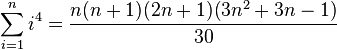 (Summe der ersten
(Summe der ersten  Potenzen mit Exponenten 4)
Potenzen mit Exponenten 4)
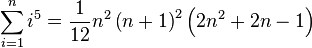 (Summe der ersten
(Summe der ersten  Potenzen mit Exponenten 5)
Potenzen mit Exponenten 5)
Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhabersche Formel
Die Integralfunktion

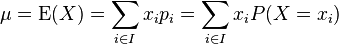
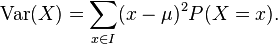
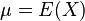 sowie die Varianz als auch die Standardabweichung!
sowie die Varianz als auch die Standardabweichung!