Lagebeziehungen von Ebenen

Zwei Ebenen können drei Lagebeziehungen haben: 1. Die beiden Ebenen E₁ und E₂ sind (echt) parallel.

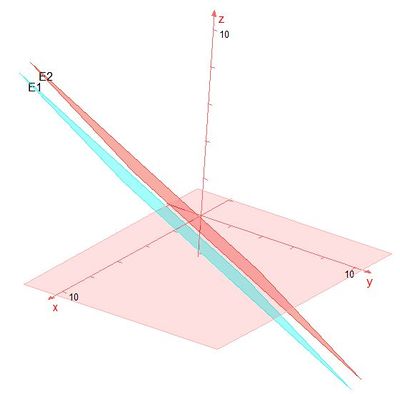
Die beiden Normalenvektoren 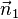$\vec{n}_1$ der Ebene E₁ und 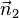$\vec{n}_2$ der Ebene E₂ sind kollinear. Es gilt 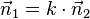$\vec{n}_1 = k\cdot \vec{n}_2$. Da k eine reelle Zahl ist, also auch negativ sein kann, können die Richtungen der beiden Normalenvektoren gleich oder entgegengesetzt sein.
Die beiden Ebenen E₁ und E₂ haben keinen Punkt gemeinsam 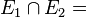$E_1\cap E_2 =${ }.

2. Die beiden Ebenen Ebenen E₁ und E₂ fallen zusammen.

Auch hier sind die beiden Normalenvektoren 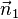$\vec{n}_1$ der Ebene E₁ und 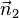$\vec{n}_2$ der Ebene E₂ kollinear. Es gilt 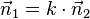$\vec{n}_1 = k\cdot \vec{n}_2$. Da k eine reelle Zahl ist, also auch negativ sein kann, können die Richtungen der beiden Normalenvektoren gleich oder entgegengesetzt sein.
Die beiden Ebenen E₁ und E₂ haben unendlich viele Punkt gemeinsam E₁=E₂.

3. Die beiden Ebenen E₁ und E₂ schneiden sich.

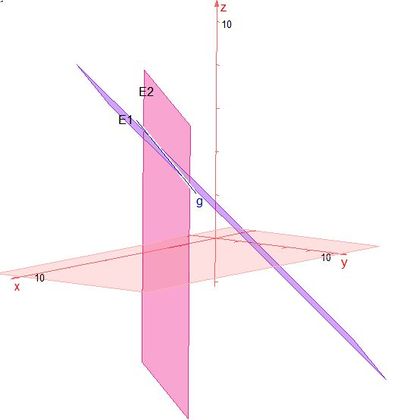
Die beiden Normalenvektoren 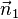$\vec{n}_1$ der Ebene E₁ und 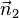$\vec{n}_2$ der Ebene E₂ sind nicht kollinear. Es gilt $\vec{n}_1 \neq k\cdot \vec{n}_2$.
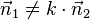Die beiden Ebenen E₁ und E₂ haben eine Gerade g gemeinsam 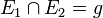$E_1\cap E_2 = g$, die Schnittgerade.

Die drei Fälle sind auch im Buch auf S. 141 mit guten Biildern beschrieben!

Ebenen sind durch Angabe ihrer Ebenengleichung gegeben. Man kann diese drei Fälle relativ leicht lösen, wenn eine Ebene in Normalenform und die andere Ebene in Parameterform sind. Man setzt dann die Koordinaten der Parameterform in die Normalengleichung ein und erhält eine Gleichung mit zwei Parametern k und m. Dies wollen wir in den drei folgenden Beispielen sehen (ist auch im Buch S. 141 unten beschrieben!).

Beispiele:
zu 1. Die beiden Ebenen E₁: 2x₁ - x₂ - 2x₃ - 3 = 0 und die Ebene E₂: 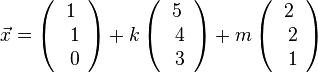$\vec{x}= \left( \begin{array}{c} 1 \\\ 1 \\\ 0 \end{array}\right) + k \left( \begin{array}{c} 5 \\\ 4 \\\ 3 \end{array}\right) + m \left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)$ sind echt parallel.

[Lösung anzeigen][Lösung ausblenden]

Im Buch auf S. 143 ist diese Aufgabe in der unteren Hälfte gelöst. Es werden zwei Lösungswege angeboten:
Die Koordinaten der Parameterform werden in die Normalenform eingesetzt. Terme mit k und m heben sich auf und es führt zu einer falschen Aussage -2 = 0, dies bedeutet, dass die Gleichung keine Lösung hat. Also besitzen die beiden Ebenen E₁ und E₂ keinen gemeinsamen Punkt uns sind echt parallel.

Das Bild bei 1. stellt diese Ebenen dar.

zu 2. Die beiden Ebenen E₁: 2x₁ - x₂ - 2x₃ - 1 = 0 und die Ebene E₂: 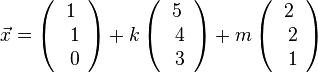$\vec{x}= \left( \begin{array}{c} 1 \\\ 1 \\\ 0 \end{array}\right) + k \left( \begin{array}{c} 5 \\\ 4 \\\ 3 \end{array}\right) + m \left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right)$ sind identisch. Sie fallen zusammen.

[Lösung anzeigen][Lösung ausblenden]

Es hat sich für die Ebene E₁ die Konstante geändert. Dies bedeutet, dass die Ebene verschoben wuwrde.
Auch hier gibt es zwei Möglichkeiten für die Lösung:
1. Möglichkeit:
Man setzt die Koordinaten der Parametergleichung in die Normalenform ein.
2(1+5k+2m) - (1+4k+2m) - 2(3k+m) - 1 = 0
2 + 10k + 4m -1 -4k -2m -6k - 2m - 1= 0
0 = 0 Dies ist eine allgemeingültige Gleichung, die unendlich viele Lösungen hat, also ist E₁ = E₂.
2. Möglichkeit:
Der Normalenvektor der Ebene E₁ ist 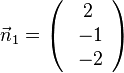$\vec{n}_1= \left( \begin{array}{c} 2 \\\ -1 \\\ -2 \end{array}\right)$. Den Normalenvektor der Ebene E₂ erhält man mit dem Kreuzprodukt $\vec{n}_2= \left( \begin{array}{c} 5 \\\ 4 \\\ 3 \end{array}\right) \times \left( \begin{array}{c} 2 \\\ 2 \\\ 1 \end{array}\right) = \left( \begin{array}{c} -2 \\\ 1 \\\ 2 \end{array}\right)$ .
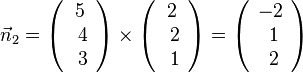Man sieht, dass 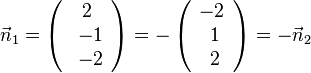$\vec{n}_1= \left( \begin{array}{c} 2 \\\ -1 \\\ -2 \end{array}\right) = -\left( \begin{array}{c} -2 \\\ 1 \\\ 2 \end{array}\right) = -\vec{n}_2$ ist. Also sind die beiden Normalenvektoren kollinear.
Nun prüft man noch, ob der Stützpunkt A(1;1;0) der Ebene E₂ in der Ebene E₁ liegt, also 2·1 - 1·1 - 2·0 - 1 = 0. Somit liegt A auch in der Ebene E₁ und die beiden Ebenen E₁ und E₂ sind identisch.

Das Bild bei 2. stellt diese Ebenen dar.

zu 3. 2. Die beiden Ebenen E₁: 2x₁ - x₂ - 2x₃ - 1 = 0 und die Ebene E₂: 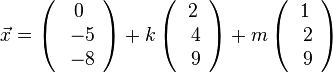$\vec{x}= \left( \begin{array}{c} 0 \\\ -5 \\\ -8 \end{array}\right) + k \left( \begin{array}{c} 2 \\\ 4 \\\ 9 \end{array}\right) + m \left( \begin{array}{c} 1 \\\ 2 \\\ 9 \end{array}\right)$ schneiden sich. Ermitteln Sie die Gleichung der Schnittgerade g.

[Lösung anzeigen][Lösung ausblenden]

Die Lösung hierzu finden Sie im Buch auf S. 142. Es ist das mittlere Beispiel. Man setzt die Koordinaten der Parametergleichung in die Normalenform und löst die Gleichung nach einem Parameter k oder m auf.
Es ergibt sich z.B. m = 1 - k. Nun setzt man für m in die Gleichung der Ebene E₂ (Parameterform) 1-k und fasst die Vektoren mit k zusammen und erhält damit die Gleichung der Schnittgeraden g. (Dies ist in der Lösung im Buch ausführlich dargestellt.)

Das Bild bei 3. stellt diese Ebenen dar.