M10 Exponentielles Wachstum: Unterschied zwischen den Versionen
| Zeile 229: | Zeile 229: | ||
{{Aufgaben-blau|10|2=Buch S. 90 / 12 }} | {{Aufgaben-blau|10|2=Buch S. 90 / 12 }} | ||
| − | {{Lösung versteckt|1=a) Der Wachstumsfaktor ist 1 + 5% = 1,05. Die exponentielle Wachstumsfunktion ist <math>f(x) = 60 \cdot 1,05^x</math>. | + | {{Lösung versteckt|1=a) Der Wachstumsfaktor ist 1 + 5% = 1,05. Die exponentielle Wachstumsfunktion ist <math>f(x) = 60 \cdot 1,05^x</math>. |
| + | |||
b) <math>f(2008-1626)=f(382)=60 \cdot 1,05^{382}=7455272036</math>, also circa 7,5 Milliarden Gulden. <br> | b) <math>f(2008-1626)=f(382)=60 \cdot 1,05^{382}=7455272036</math>, also circa 7,5 Milliarden Gulden. <br> | ||
| − | Der Preis pro m<sup>2</sup> ist dann <math>\frac{7455272036 Gulden}{60\cdot 10^6 m^2} = 124,25 \frac{Gulden}{m^2}</math>. | + | Der Preis pro m<sup>2</sup> ist dann <math>\frac{7455272036 Gulden}{60\cdot 10^6 m^2} = 124,25 \frac{Gulden}{m^2}</math>. |
| + | |||
c) Heute kostet 1m<sup>2</sup> in Manhatten über [https://www.sueddeutsche.de/geld/immobilienpreise-in-new-york-10-000-dollar-pro-quadratmeter-1.545145 10000$]. <br> | c) Heute kostet 1m<sup>2</sup> in Manhatten über [https://www.sueddeutsche.de/geld/immobilienpreise-in-new-york-10-000-dollar-pro-quadratmeter-1.545145 10000$]. <br> | ||
| − | |||
Eine Kuh kostet etwa [https://www.tagesspiegel.de/wirtschaft/nicht-alltaeglich-was-kostet-eigentlich-eine-kuh/11572788.html 1800€]. Also entspricht der Kaufpreis von 60 Gulden damals 6 Kühen und heute 108000€. <br> | Eine Kuh kostet etwa [https://www.tagesspiegel.de/wirtschaft/nicht-alltaeglich-was-kostet-eigentlich-eine-kuh/11572788.html 1800€]. Also entspricht der Kaufpreis von 60 Gulden damals 6 Kühen und heute 108000€. <br> | ||
Version vom 26. Februar 2021, 08:50 Uhr
Im März 2020 wurde der erste Lockdown zur Corona-Pandemie mit der exponentiellen Zunahme der Infizierten und Kranken begründet. Was heißt aber nun exponentielle Zunahme?
Was ist nun anders?
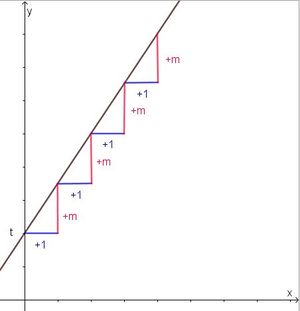
In der 8. Klasse hat man das lineare Wachstum kennengelernt. Ein Anfangsbestand t erfährt pro Zeiteinheit eine Zunahme um m. y kennzeichnet den Gesamtbestand nach x Zeiteinheiten.
|
Es ergibt sich die Formel y = mx + t , der Graph ist eine Gerade mit y-Abschnitt t und Steigung m.
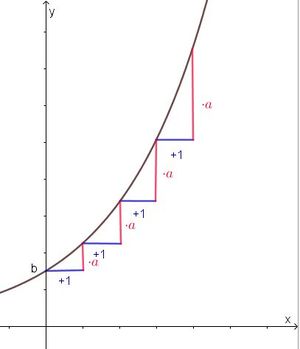
Beim exponentiellen Wachstum ist es ähnlich, nur dass nun nach jeder Zeiteinheit der Bestand mit dem Wachstumsfaktor a multipliziert wird. Während jeder Zeiteinheit ändert sich der Bestand um den gleichen Faktor a. Man hat dann diese Tabelle.
|
Es ergibt sich die Formel y = b·ax mit b ist der Anfangsbestand und a ist der Wachstumsfaktor.
Ist a > 1, dann liegt eine exponentielle Zunahme vor, ist a < 1 dann eine exponentielle Abnahme.
In diesem Video wird das exponentielle Wachstum zuerst wieder am Schachproblem mit den Reiskörner begonnen und dann bei Corona betrachtet. Viele Aussagen und Bilder zu Corona werden euch sicher aus diversen Informationssendungen bekannt vorkommen.
a) lineares Wachstum
b) lineares Wachstum (Winkelsumme im n-Eck = (n-2)180°)
c) exponentielles Wachstum
d) lineares Wachstum
e) exponentielles Wachstum
|
Merke:
Vervielfacht sich ein Bestand pro Einheit jeweils um den gleichen Faktor a, dann spricht man von einem exponentiellen Wachsstum. |
Wenn man den Anfangsbestand b hat und er nimmt jeweils pro Einheit von x um 50% zu, dann ist der Wachstumsfaktor 1,5.
Nach einer Einheit ist y = b·1,5, hat also um 50% zugenommen. Dies ist nun der Ausgangswert für die nächste Einheit. Nach dieser Einheit ist der Bestand y = (b·1,5)·1,5=b·1,52. Dies ist nun der Ausgangswert für die nächste Einheit. Nach der dritten Einheit ist der Bestand y = (b·1,52)·1,5 = b·1,53. usw.
Wenn die Zunahme um 50% (= 0,5) ist, dann ist der Wachstumsfaktor 1 + 0,5 = 1,5.
Ist die Zunahme pro Einheit 30%, dann ist der Wachstumsfaktor a = 1,3. Bei Zunahme ist a > 1.
Bei einer Abnahme um 20%, verringert sich der Anfangsbestand. Nach der ersten Einheit sind nur noch 80% vorhanden. Der Anfangsbestand b ist dann y = b·0,8. Dies ist wieder der Ausgangswert für die nächste Einheit. Nach der zweiten Einheit ist deren Anfangsbestand b·0,8 dann nur noch y = (b·0,8)·0,8 = b·0,8<sup<2</sup>. Dies ist dann der Ausgangswert für die nächste Einheit. Nach der dritten Einheit ist der Bestand y = (b·0,82)·0,8 = b·0,853. usw.
Wenn die Abnahme pro Einheit 20% (=0,2) ist, dann ist der Wachstumsfaktor 1 - 0,2 = 0,8.
Ist die Abnahme pro Einheit 30%, dann ist der Wachstumsfaktor a = 0,7. Bei Abnahme ist a < 1.
|
Der Wachstumsfaktor a ist stets eine positive reelle Zahl, also a > 0. Hat man eine Zunahme, dann ist a > 1, hat man eine Abnahme, dann ist a < 1. |
Beispiel: Franziska bekommt von ihrem Lieblingonkel Franz ein Sparbuch mit 1000€. Pro Jahr wird ihr Kapital mit 5% verzinst. Der Zins wird zum Jahresende berechnet, sein Betrag ist 1000€·5%=1000€·0,05 und zum Kapital hinzugerechnet.
Nach dem ersten Jahr hat Franziska dann 1000€ + 1000€·5%=1000€ + 1000€*0,05 = 1000€ + 50€.
Andere Rechnung mit dem Distributivgesetz: 1000€ + 1000€*0,05 = 1000€·(1+0,05) = 1000€·1,05 = 1050€.
Dies ist jetzt das Kaptial für das zweite Jahr. Nach dem zweiten Jahr hast Franziska dann 1050€ + 1050€·0,05 = 1050€·1,05 = 1102,50€
Nach dem dritten Jahr erhältst sie wieder Zinsen und ihr Kapital ist dann 1102,50€ + 1102,50€·0,5 = 1102,50€·1,05 = 1157,625€. (Der halbe Cent wird aufgerundet!). usw.
Für die ersten 5 Jahre schaut das so aus:
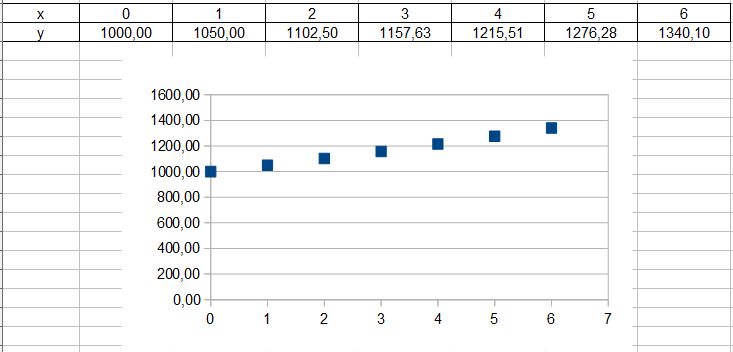
Das ist jetzt nicht aufregend. Bei linearem Wachstum hättest du nur 1000€ + 5·50€ = 1250€. Da ist dieses exponentielle Wachstum schon etwas besser. Man sieht den Effekt des exponentiellen Wachstums besser, wenn man weiter fortschreitet.
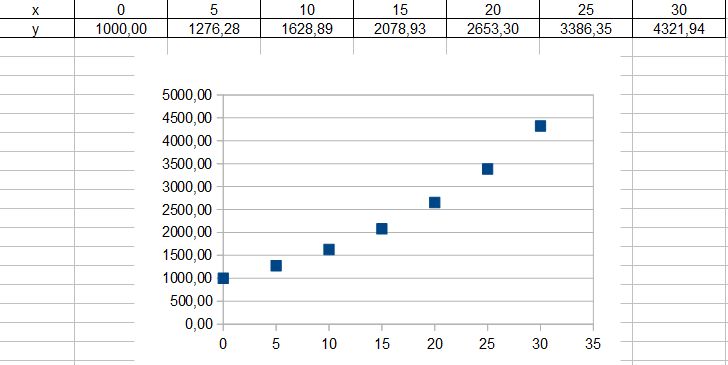
Hier sieht man im Diagramm deutlich wie das Kapital doch deutlich größer wird. Nach 30 Jahren hättest du mit linearem Wachstum 2500€. Bei exponentiellem Wachstum ist es doch deutlich mehr. Man bezeichnet dies auch als Zinseszinseffekt.
Am 1.1.2021 wäre ihr Vermögen 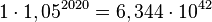 in der Einheut €.
in der Einheut €.
|
Ist die Zunahme pro Einheit p%, dann ist der Wachstumsfaktor a = 1+p/100. Ist die Abnahme pro Einheit p%m dann ist der Wachstumsfaktor a = 1-p/100. |
Das sind zwei Beispiele für exponentielle Zunahme.
87/3
a) Der Wachstumsfaktor ist 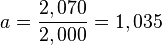
Die Anzahl nimmt pro Minute um 3,5% zu.
b) Du erhältst den ersten Wert von N für t = 1, indem du den Wert N(0) mit 1,035 multiplizierst.
Du erhältst den Wert N(2) von N für t = 2, indem du den Wert N(1)=2,070 mit 1,035 mulitplizierst.
du erhälst den WErt N(3) von N für t = 3, indem du den Wert N(2)=2,1425 mit 1,035 multiplizierst.
....
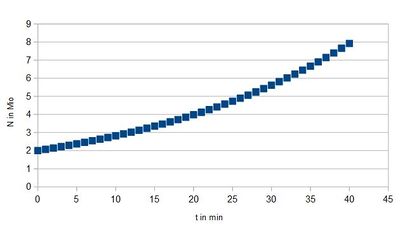
Interessant wird es für t = 20, t = 30, t = 40.
Hier erhältst du den Wert N(20) von N für t = 20, indem du den Wert N(0) mit 1,03520 multiplizierst.
Den Wert N(30) erhältst du, indem du den Wert N(0) mit 1,03530 multiplizierst.
Die Gleichung für N(t) ist N(t)=N(0)·1,035t
![]()
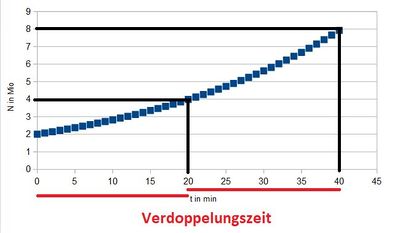
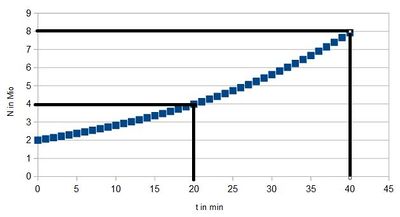
Aus dem Diagramm liest man ab, wenn man bei 4 auf der N-Achse waagrecht nach rechts geht und bei dem eingezeichneten Punkt, den man dann trifft nach unten, dass sich der Anfangsbestand nach 20 Minuten etwa verdoppelt hat. Nach 40 Minuten hat er sich vervierfacht.
87/4
a) ![]()
b) 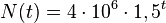
c) 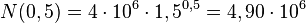
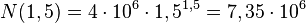
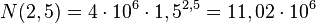
d) In einer ersten halben Stunden hat die Bakterienkultur um 0,9 Millionen zugenommen, das sind 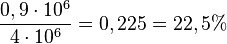 .
.
In der zweiten halben Stunde hat die Bakterienkultur um 1,1 Millionen zugenommen, das sind 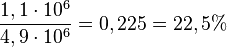 .
.
In der dritten halben Stunde hat die Bakterienkultur um 1,35 Millionen zugenommen, das sind 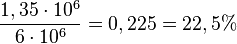 .
.
In der vierten halben Stunde hat die Bakterienkultur um 1,65 Millionen zugenommen, das sind 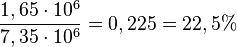 .
.
In der fünften halben Stunde hat die Bakterienkultur um 2,02 Millionen zugenommen, das sind 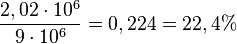 .
.
In der sechsten halben Stunde hat die Bakterienkultur um 2,48 Millionen zugenommen, das sind 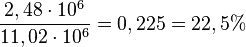 .
.
e) 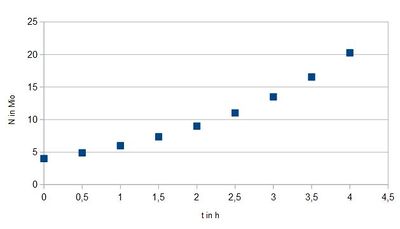
Zum Ablesen der Verdoppelungszeit nimmt man einen Wert her z.B. für t=0h und N(0)=4·106 und sucht im Diagramm den Zeitpunkt t1, wenn N(t1=8·106 ist. (schwarz im Diagramm) Man liest etwa für die Verdoppelungszeit T=1,8h ab.
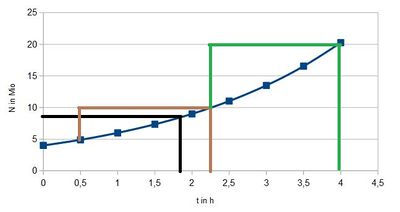
Der braune Weg ist für die Verdoppelung von 5 Millionen auf 10 Millionen und man liest ab T = 2,25h - 0,5h = 1,75h.
Der grüne Weg ist für die Verdoppelung von 10 Millionen auf 20 Millionen und man liest ab T = 4h - 2,25h=1,75h.
f) Hier hat man zwei Möglichkeiten. Entweder man erweitert das Diagramm nach links und liest aus dem Diagramm den Wert für t = - 0,5h ab.
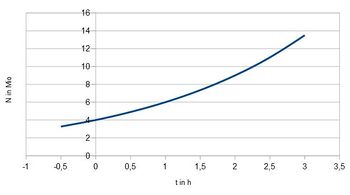 N(-0,5h)=3,3·106
N(-0,5h)=3,3·106
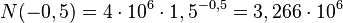
Dies ist jetzt ein Beispiel für exponentielle Abnahme.
Hinweis: 1dm = 10cm
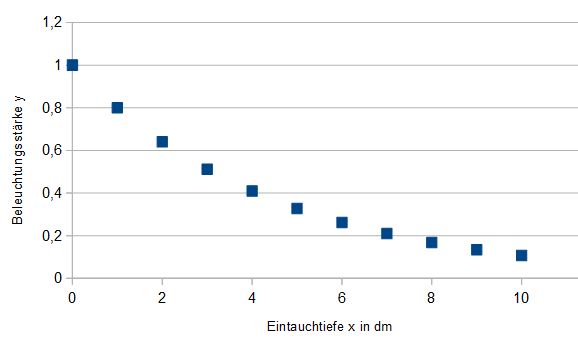
a) Pro 1dm nimmt die Beleuchtungsstärke um 20% ab, d.h. in 10cm Tiefe ist nur noch 80% des Lichtes an der Oberfläche vorhanden, also 1·0,8=0,8. Nach dem nächsten 1dm ist man in 2cm Tiefe und dort ist dann nur noch 80% des Lichts von 10cm Tiefe, also 0,8·0,8 = 0,64 = 64% vorhanden, usw.
x gibt die Eintauchtiefe in dm an, y die Beleuchtungsstärke in der Tiefe x bezogen auf die Beleuchtungsstärke an der Oberfläche, also eine relative Beleuchtungsstärke in der Tiefe x.
![]()
Das Diagramm dazu schaut so aus.
b)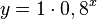
c) Aus dem Diagramm
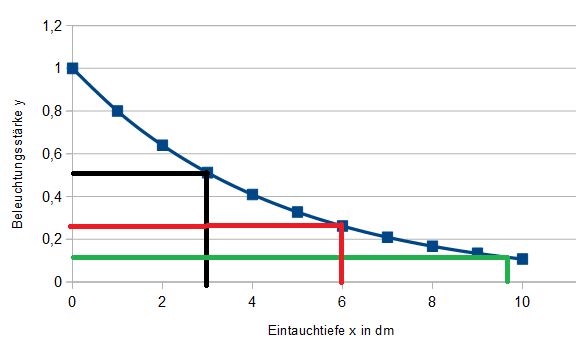
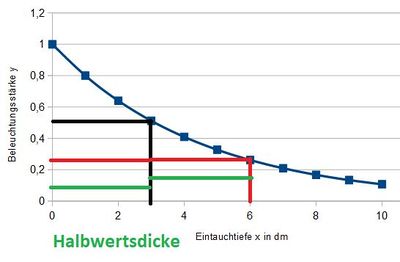
kann man ablesen, dass in 3dm Tiefe die Beleuchtungsstärke auf die Hälfte (schwarz),in 6dm Tiefe auf ein Viertel (rot) und in 9,7dm auf ein Achtel (grün) abgenommen hat.
Aus der Tabelle kann man für die Abnahme auf die Hälfte nach etwas mehr als 3dm erfolgt, die Abnahme auf ein Viertel nach etwas mehr als 6dm und auf ein Achtel mehr als 9dm. (Der grüne abgelesene Wert aus dem Diagramm wird etwas falsch liegen!)
1. Aus dem Graph würde man eine Halbwertsdicke beim Halbieren und Vierteln von 3dem ablesen.
Aus der Rechnung erhält man die Halbwertszeit 3,1dm.
2. Aus der Physik der 9. Klasse kennst du den radioaktiven Zerfall.
Beim radioaktiven Zerfall gibt die Halbwertszeit an, nach welcher Zeit die Hälfte der radioaktiven Kerne zerfallen ist.
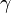 -Strahlung noch die Hälfte der
-Strahlung noch die Hälfte der 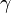 -Strahlung vorhanden ist.
-Strahlung vorhanden ist.
a) a = 1,2
b) a = 1,07
c) a = 1.003
d) a = 0,85
e) a = 0,875
f) a = 0,9975
g) a = 2
h) a = 3
i) a = 2,25
k) Zunahme um 4%
l) Zunahme um 60%
m) Abnahme um 5%
n) Zunahme um 150%
o) Abnahme um 50%
p) Abnahme um 0,1%
q) Zunahme um 30%
a) In der dritten Zeile berechnet man die Änderung, indem man die Masse von x = 1 - Masse von x = 2 berechnet, usw. . Der Wachstumsfaktor ist 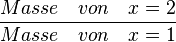 , usw.
, usw.

b) Der Wachstumsfaktor ist stets gleich 0,8.
c) 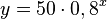
d) Mit der Gleichung aus b) 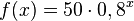 erhält man
erhält man 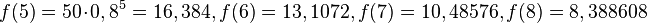 .
.
e) 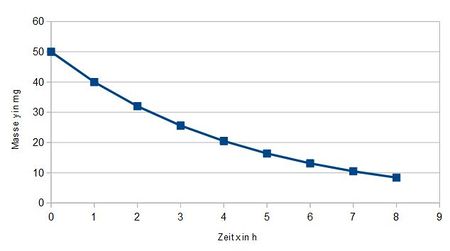
Aus dem Diagramm
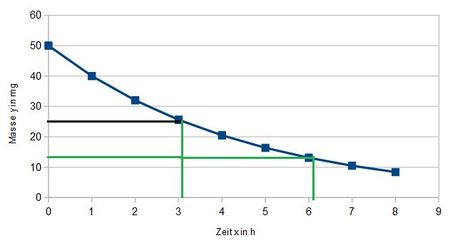
liest man ab, dass nach 3,1h die Koeffeinmenge halbiert und nach 6,2h geviertelt ist.
f) Nach einer halben Stunde hat man 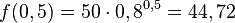 mg Koeffin im Blut
mg Koeffin im Blut
.
Trinkt man eine Tasse und eine halbe Stunde später noch eine Tasse Kaffee, dann hat man 50mg(2. Tasse) + 44,7mg(1. Tasse) = 94,7mg Koffein im Blut.
Trinkt man eine halbe Stunde später noch eine Tasse, dann hat man 50mg(3. Tasse) + 44,7mg(2. Tasse) + 40mg(1. Tasse) = 134,7mg Koeffein im Blut.
Trinkt man eine halbe Stunde später noch eine Tasse, dann hat man von der ersten Tasse noch 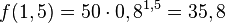 mg Koeffein im Blut uns insgesamt 50mg + 44,7mg + 40mg + 35,8mg = 170,5mg.
mg Koeffein im Blut uns insgesamt 50mg + 44,7mg + 40mg + 35,8mg = 170,5mg.
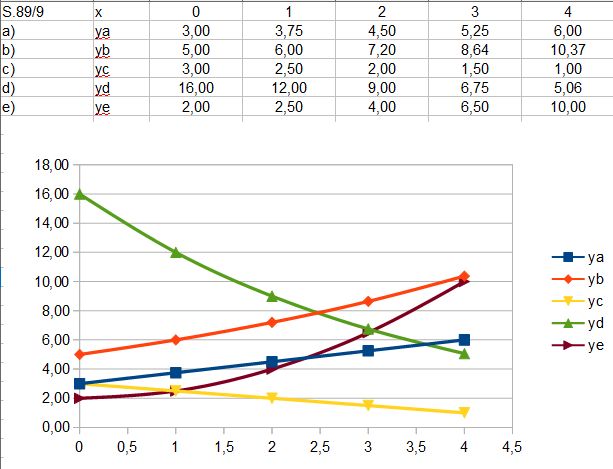
a) lineares Wachstum y = 0,75x + 3 (Zunahme)
b) exponentielles Wachstum y = 5·1,2x (Zunahme)
c) lineares Wachstum y = -0,5x + 3 (Abnahme)
d) exponentielles Wachstum y = 16·0,75x (Abnahme)
a) Der Wachstumsfaktor ist 1 + 5% = 1,05. Die exponentielle Wachstumsfunktion ist 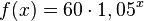 .
.
b) 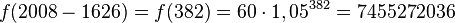 , also circa 7,5 Milliarden Gulden.
, also circa 7,5 Milliarden Gulden.
Der Preis pro m2 ist dann 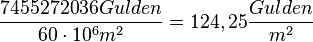 .
.
c) Heute kostet 1m2 in Manhatten über 10000$.
Eine Kuh kostet etwa 1800€. Also entspricht der Kaufpreis von 60 Gulden damals 6 Kühen und heute 108000€.
Mit Verzinsung hätte man 2008 also 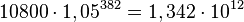 €, also 1342 Milliarden Euro. Dafür bekäme man heute in Manhatten 134km2, also mehr als die doppelte Fläche von Manhatten.
€, also 1342 Milliarden Euro. Dafür bekäme man heute in Manhatten 134km2, also mehr als die doppelte Fläche von Manhatten.
Aus heutiger Sicht war das wohl ein fairer Deal.
1. Entfernung vom Startpunkt:
Bei jedem Schritt +10 auf der (waagrechten) Zeitachse wird die Entfernung von dem Startpunkt verzehnfacht, also ·10. Dies entspricht einem exponentiellen Wachstum, da nach zwei Schritten (nach 20s) man bereits die Entfernung ·10·10=·100 hat. Der urprüngliche Bildausschnitt war 1m x 1m, nach 10s ist er 10m x 10m, nach weitern +10s (also nach 20s) ist er 100m x 100m, nach weiteren +10s (also nach 30s) ist er 1000m x 1000m, ....
Auf der waagrechten Zeitachse kommen immer +10s dazu, während auf der senkrechten Entfernungsachse immer mit 10 multipliziert wird.
2. Rückkehr zum Startpunkt:
Bei jedem Schritt +2 wird die Entfernung vom neuen Startpunkt im Weltall gezehntelt. Also ist der Wachstumsfaktor 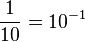 . Auf der Zeitachse kommen immer 2s dazu, während die Entfernung dabei um neun Zehntel abnimmt.
. Auf der Zeitachse kommen immer 2s dazu, während die Entfernung dabei um neun Zehntel abnimmt.
3. Näherung an den Atomkern:
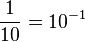 .
.

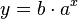 ,
,