M10 Exponentielles Wachstum und Logarithmen: Unterschied zwischen den Versionen
| Zeile 33: | Zeile 33: | ||
{{Lösung versteckt|1=Algen- und Bakterienwachstum, Zinseszins, Koffeinabbau im Blut }} | {{Lösung versteckt|1=Algen- und Bakterienwachstum, Zinseszins, Koffeinabbau im Blut }} | ||
| + | |||
| + | {{Aufgaben-blau|2|2=Buch S. 86 / 2 }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) lineares Wachstum<br> | ||
| + | b) lineares Wachstum (Winkelsumme im n-Eck = (n-2)180°)<br> | ||
| + | c) exponentielles Wachstum<br> | ||
| + | d) lineares Wachstum<br> | ||
| + | e) exponentielles Wachstum<br> | ||
| + | f) lineares Wachsstum }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Buch S. 87 / 3, 4 }} | ||
| + | |||
| + | {{Lösung versteckt|1=87/3<br> | ||
| + | a) Der Wachstumsfaktor ist <math>a = \frac{2,070}{2,000}=1,035</math><br> | ||
| + | Die Anzahl nimmt pro Minute um 3,5% zu.<br> | ||
| + | b) Du erhältst den ersten Wert von N für t = 1, indem du den Wert N(0) mit 1,035 multiplizierst. <br> | ||
| + | Du erhältst den Wert N(2) von N für t = 2, indem du den Wert N(1)=2,070 mit 1,035 mulitplizierst. <br> | ||
| + | du erhälst den WErt N(3) von N für t = 3, indem du den Wert N(2)=2,1425 mit 1,035 multiplizierst.<br> | ||
| + | ....<br> | ||
| + | Interessant wird es für t = 20, t = 30, t = 40.<br> | ||
| + | Hier erhältst du den Wert N(20) von N für t = 20, indem du den Wert N(0) mit 1,035<sup>20</sup> multiplizierst.<br> | ||
| + | Den Wert N(30) erhältst du, indem du den Wert N(0) mit 1,035<sup>30</sup> multiplizierst. | ||
| + | Die Gleichung für N(t) ist N(t)=N(0)·1,035<sup>t</sup> | ||
| + | [[Datei:87-3.jpg]]<br> | ||
| + | }} | ||
Version vom 1. Februar 2021, 20:03 Uhr
Im März 2020 wurde der erste Lockdown zur Corona-Pandemie mit der exponentiellen Zunahme der Infizierten und Kranken begründet. Was heißt aber nun exponentielle Zunahme?
Was ist nun anders?
In der 8. Klasse hat man das lineare Wachstum kennengelernt. Ein Anfangsbestand t erfährt pro Zeiteinheit eine Zunahme um m. y kennzeichnet den Gesamtbestand nach x Zeiteinheiten.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | t | t+m | t+2m | t+3m | t+4m | t+5m |
Es ergibt sich die Formel y = mx + t , der Graph ist eine Gerade mit y-Abschnitt t und Steigung m.
Beim exponentiellen Wachstum ist es ähnlich, nur dass nun nach jeder Zeiteinheit der Bestand mit dem Wachstumsfaktor a multipliziert wird. Während jeder Zeiteinheit ändert sich der Bestand um den gleichen Faktor a. Man hat dann diese Tabelle.
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| y | b | b·a | b·a2 | b·a3 | b·a4 | b·a5 |
Es ergibt sich die Formel y = b·ax mit b ist der Anfangsbestand und a ist der Wachstumsfaktor.
Ist a > 1, dann liegt eine exponentielle Zunahme vor, ist a < 1 dann eine exponentielle Abnahme.
In diesem Video wird das exponentielle Wachstum zuerst wieder am Schachproblem mit den Reiskörner begonnen und dann bei Corona betrachtet. Viele Aussagen und Bilder zu Corona werden euch sicher aus diversen Informationssendungen bekannt vorkommen.
a) lineares Wachstum
b) lineares Wachstum (Winkelsumme im n-Eck = (n-2)180°)
c) exponentielles Wachstum
d) lineares Wachstum
e) exponentielles Wachstum
87/3
a) Der Wachstumsfaktor ist 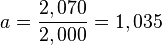
Die Anzahl nimmt pro Minute um 3,5% zu.
b) Du erhältst den ersten Wert von N für t = 1, indem du den Wert N(0) mit 1,035 multiplizierst.
Du erhältst den Wert N(2) von N für t = 2, indem du den Wert N(1)=2,070 mit 1,035 mulitplizierst.
du erhälst den WErt N(3) von N für t = 3, indem du den Wert N(2)=2,1425 mit 1,035 multiplizierst.
....
Interessant wird es für t = 20, t = 30, t = 40.
Hier erhältst du den Wert N(20) von N für t = 20, indem du den Wert N(0) mit 1,03520 multiplizierst.
Den Wert N(30) erhältst du, indem du den Wert N(0) mit 1,03530 multiplizierst.
Die Gleichung für N(t) ist N(t)=N(0)·1,035t

