M10 Grenzwert und Polynomfunktionen
Wir betrachten zuerste das Verhalten von Potenzfunktionen f mit f(x) = xn, wobei n eine natürliche Zahl ist.
|
Der Grenzwert von allen Potenzfunktionen f mit f(x) = xn ist für Der Grenzwert für
|
|
Merke:
Ein Term anxn + an-1xn-1 + ... + a1x + a0 mit reellen Zahlen an, an-1, ... , a1, a0 und an
|
Beispiel: 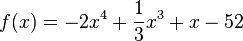
Der Grad von f(x) ist 4, da die höchste x-Potenz x4 ist.
Die Koeffizienten sind a4 = -2, a3 =  , a1 = 1, a0 = -52.
, a1 = 1, a0 = -52.
Da im Polynom kein Summand mit x2 vorkommt ist a2 = 0, was man nicht extra notiert.
|
Merke:
Der Grenzwert von Polynomfunktionen f vom Grad n wird durch die höchste x-Potenz xn bestimmt. Bei den Polynomfunktionen geraden Grade ist das Vorzeichen der beiden Grenzwerte für Ihr Koeffizient an bestimmt dann das Vorzeichen der Grenzwerte. |
Im folgenden Applet ist der Graph einer Polynomfunktion 3. Grades f mit f(x) = ax3 - 2x2 + x + 1 dargestellt. Mit dem Schieberegler kann man den Wert von a von +1 auf -1 ändern.
Zur Begründung, dass der Koeffizient an der größten x-Potenz xn den Grenzwert festlegt:
Es ist 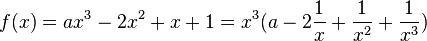 . Die Brüche in der Klammer gehen alle für
. Die Brüche in der Klammer gehen alle für  gegen 0. Es ist also
gegen 0. Es ist also 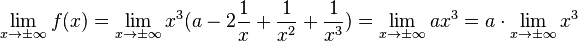 .
.
Hier sieht man, dass das Vorzeichen von a den Verlauf von Gf für 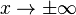 festlegt.
festlegt.
a) Der Grad der Polynomfunktion ist 2,also gerade. Deshalb ist der Grenzwert für 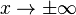 in beiden Fällen gleich. Das Vorzeichen des Koeffizienten 2 von x2 ist positiv, also ist
in beiden Fällen gleich. Das Vorzeichen des Koeffizienten 2 von x2 ist positiv, also ist 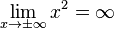
b) Der Grad der Polynomfunktion ist 7, also ungerade. Deshalb ist der Grenzwert für  und
und 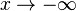 jeweils verschieden. Das Vorzeichen des Koeffizienten -3 von x7 ist negativ, also ist
jeweils verschieden. Das Vorzeichen des Koeffizienten -3 von x7 ist negativ, also ist 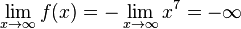 und
und 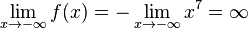
c) Der Grad der Polynomfunktion ist 1, also ungerade. Deshalb ist der Grenzwert für  und
und 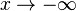 jeweils verschieden. Das Vorzeichen des Koeffizienten 1 von x ist positiv, also ist
jeweils verschieden. Das Vorzeichen des Koeffizienten 1 von x ist positiv, also ist 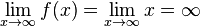 und
und 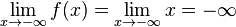
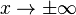 in beiden Fällen gleich. Das Vorzeichen des Koeffizienten 2 von x2 ist positiv, also ist
in beiden Fällen gleich. Das Vorzeichen des Koeffizienten 2 von x2 ist positiv, also ist 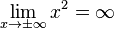
Mehr über Polynomfunktionen findest du hier.
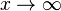 :
: 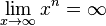
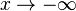 ist, wenn
ist, wenn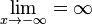
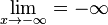

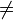 0 ist ein Polynom vom Grad n.
0 ist ein Polynom vom Grad n.
