M9 Aufgaben zur Trigonometrie: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 36: | Zeile 36: | ||
{{Aufgaben-blau|2|2=1. Löse <math>(sin(\alpha))^2 + (cos(\alpha))^2 = 1</math> nach <math>sin(\alpha)</math> bzw. <math>cos(\alpha)</math> auf. | {{Aufgaben-blau|2|2=1. Löse <math>(sin(\alpha))^2 + (cos(\alpha))^2 = 1</math> nach <math>sin(\alpha)</math> bzw. <math>cos(\alpha)</math> auf. | ||
| − | 2. | + | 2. Berechne ohne Ermittlung des Winkels <math>\varphi</math> für <br> |
| − | }} | + | a) <math>sin(\varphi)= 0,25</math> die Werte von <math>cos(\varphi), tan(\varphi)</math>.<br> |
| + | b) <math>cos(\varphi)= 0,5</math> die Werte von <math>sin(\varphi), tan(\varphi)</math>.<br> | ||
| + | c) <math>tan(\varphi)= 1</math> die Werte von <math>sin(\varphi), cos(\varphi)</math>.<br> | ||
| + | d) <math>sin(\varphi)= 0,11</math> die Werte von <math>cos(\varphi), tan(\varphi)</math>.<br> | ||
| + | e) <math>cos(\varphi)= 0,72</math> die Werte von <math>sin(\varphi), tan(\varphi)</math>.<br> | ||
| + | f) <math>sin(\varphi)= 0,5</math> die Werte von <math>cos(\varphi), tan(\varphi)</math>.<br> }} | ||
| − | {{Lösung versteckt|1=1. <math>sin(\alpha)=\sqrt {1-(cos(\alpha))^2}</math><br> | + | {{Lösung versteckt|1=1. <math>sin(\alpha)=\sqrt {1-(cos(\alpha))^2}</math> , <math>cos(\alpha)=\sqrt {1-(sin(\alpha))^2}</math><br> |
| − | <math>cos(\alpha)=\sqrt {1-(sin(\alpha))^2}</math> | + | 2. a)<math>cos(\alpha)=\sqrt {1-(sin(\alpha))^2}=\sqrt {1-(0,25)^2}=0968</math><br> |
| + | <math>tan(\varphi)=\frac{sin(\varphi)}{cos(\varphi)}=\frac{0,25}{0,968}=0,258</math> | ||
| + | |||
| + | b) <math>sin(\varphi)=\sqrt {1-(cos(\alpha))^2}=\sqrt {1-0,5^2}=0,866</math><br> | ||
| + | <math>tan(\varphi)=\frac{sin(\varphi)}{cos(\varphi)}=\frac{0,866}{0,5}=1,732</math> | ||
| + | |||
| + | c) <math>tan(\varphi)= 1</math> bedeutet <math>\varphi = 445^o</math> und <math>sin(45^o)=cos(45^o)= \frac{1}{2}\sqrt 2</math> | ||
| + | |||
| + | d) <math>cos(\varphi)=0,994, tan(\varphi)=0111</math> | ||
| + | |||
| + | e) <math>sin(\varphi)=0,694, tan(\varphi)=0,964</math> | ||
| + | |||
| + | f) <math>cos(\varphi)=0,866, tan(\varphi)=0577</math> }} | ||
Version vom 21. April 2021, 14:26 Uhr
Ordne richtig zu
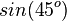 |
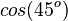
|
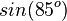 |
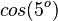
|
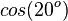 |
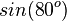
|
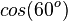 |
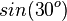
|
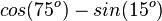 |
0 |
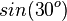 |
0,5 |
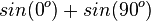 |
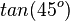
|
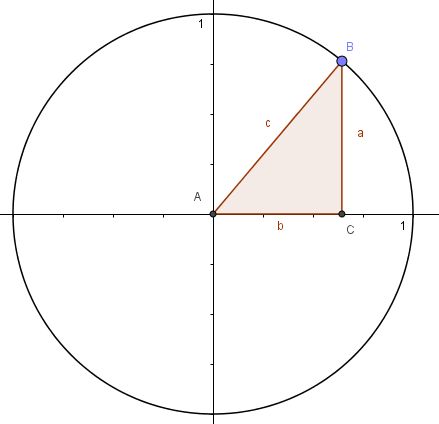
1. Es ist c = 1, da c ein Radius ist.
2. 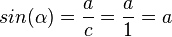
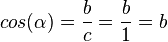
3. 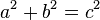
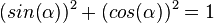
|
Merke:
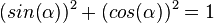 |
1. 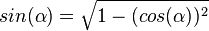 ,
, 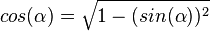
2. a)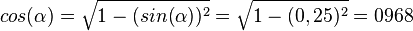
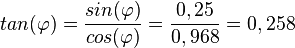
b) 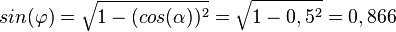
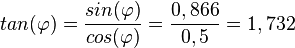
c) 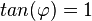 bedeutet
bedeutet 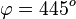 und
und 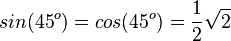
d) 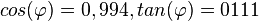
e) 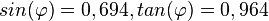
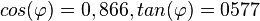
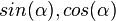 .
3. Stelle die Gleichung zum Satz des Pythagoras auf. Verwende die Ergebnisse von 1. und 2. Welche Beziehung zwischen
.
3. Stelle die Gleichung zum Satz des Pythagoras auf. Verwende die Ergebnisse von 1. und 2. Welche Beziehung zwischen 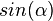 und
und 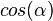 erhältst du?
erhältst du?

 für
für 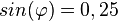 die Werte von
die Werte von 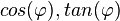 .
.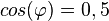 die Werte von
die Werte von 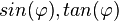 .
.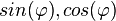 .
.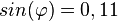 die Werte von
die Werte von 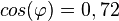 die Werte von
die Werte von 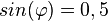 die Werte von
die Werte von 
