Mathematik - Kurs12-Heim: Unterschied zwischen den Versionen
Aus RSG-Wiki
Berny1 (Diskussion | Beiträge) (→{{Schrift grün|Stammfunktion und Unbestimmtes Integral}}) |
Berny1 (Diskussion | Beiträge) (→{{Schrift grün|Stammfunktion und Unbestimmtes Integral}}) |
||
| Zeile 6: | Zeile 6: | ||
{{Lösung versteckt|Du sollst die Aufgaben zunächst versuchen selbst zu lösen. <br>}} | {{Lösung versteckt|Du sollst die Aufgaben zunächst versuchen selbst zu lösen. <br>}} | ||
| + | |||
| + | ={{Schrift grün|Bestimmtes Integral - Einführung}}= | ||
| + | |||
| + | <ggb_applet height="500" width="800" | ||
| + | filename="UntersummeObersumme.ggb" /> | ||
| + | |||
| + | |||
| + | |||
| + | {{Kasten_blau| | ||
| + | |||
| + | [http://de.wikipedia.org/wiki/Formelsammlung_elementare_Algebra#Summenformeln Quelle: Wikipedia] | ||
| + | |||
| + | :<math> \sum_{i=1}^n i = \frac{n(n+1)}{2} </math> (Summe der ersten <math>n</math> ], Der kleine Gauß) | ||
| + | |||
| + | :<math>\sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}</math> (Summe der ersten <math>n</math> ) | ||
| + | |||
| + | :<math>\sum_{i=1}^n i^3 = \left(\frac{n(n+1)}{2}\right)^2 = \frac{n^2(n+1)^2}{4}</math> (Summe der ersten <math>n</math> Kubikzahlen) | ||
| + | |||
| + | :<math>\sum_{i=1}^n i^4 = \frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}</math> (Summe der ersten <math>n</math> Potenzen mit Exponenten 4) | ||
| + | |||
| + | :<math>\sum_{i=1}^n i^5 = \frac {1}{12} n^2 \left(n + 1\right)^2 \left(2n^2 + 2n -1\right)</math> (Summe der ersten <math>n</math> Potenzen mit Exponenten 5) | ||
| + | Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhabersche Formel|Faulhaberschen Formel berechnet werden. | ||
| + | |||
| + | }} | ||
Version vom 22. September 2013, 15:16 Uhr
Stammfunktion und Unbestimmtes Integral
Übungsblatt zur Bestimmung von Stammfunktion und unbestimmtem Integral
Du sollst die Aufgaben zunächst versuchen selbst zu lösen.
Bestimmtes Integral - Einführung
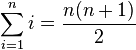 (Summe der ersten
(Summe der ersten  ], Der kleine Gauß)
], Der kleine Gauß)
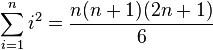 (Summe der ersten
(Summe der ersten  )
)
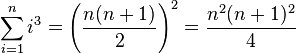 (Summe der ersten
(Summe der ersten  Kubikzahlen)
Kubikzahlen)
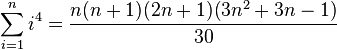 (Summe der ersten
(Summe der ersten  Potenzen mit Exponenten 4)
Potenzen mit Exponenten 4)
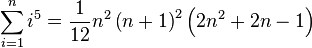 (Summe der ersten
(Summe der ersten  Potenzen mit Exponenten 5)
Potenzen mit Exponenten 5)
Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhabersche Formel


