|
Projekt der Klasse 6 d anlässlich des Tages des digitalen Lernens

Das sind wir - die Klasse 6d!
Vorbemerkung:
Das Projekt werden wir parallel zur Schulaufgabenvorbereitung in der kommenden Woche durchführen.
Ziele:
mathematische:
- Tabellen erstellen
- Prozentsätze berechnen (Division)
- Diagramme erstellen (Entscheidung für geeignete Diagrammart, Formales, Genauigkeit)
- Begriff relative Häufigkeit kennenlernen
- Einsicht in das "Gesetz der großen Zahlen" gewinnen.
ITG-Ziele
- Einblick in Tabellenkalkulation
- Einblick in Grafik-Erstellung
- Einblick in Verarbeitung digitaler Bilder
- Einblick in die Arbeit mit einem WIKI
Das Zählprinzip - Wiederholung aus Jg 5
|
|


Downloadhinweis Software
|

Tafelbild: Frau Krotsch - Foto: Lucas
|
600px
In unserem "mathematischen Laborkasten" haben wir verschiedene "Würfel", "Glücksräder" und "Münzen"
Einige Gegenstände des Laborkastens wurden am Ende der Donnerstagsstunde ausgeteilt.
|
Arbeitsaufgabe:
Entwerfe für Deinen Würfel, bzw. für Dein Glücksrad eine Tabelle wie für das Glücksrad mit den drei gleich großen Kreissektoren.
Lege die Tabelle zweimal an!
|
Glücksrad 1 mit drei gleichen Sektoren

|
Hausaufgabe:
Würfle bis zu 1000 mal Deinen Würfel und schreibe auf wie oft Du jedes Ergebnis erhalten hast bzw. drehe das Glücksrad bis zu 1000 mal und schreibe auf wie oft Du jedes Ergebnis erhalten hast.
|
|
Arbeitsaufgabe
Gib Deine Ergebnisse in die erste vorbereitete Tabelle in einer Tabellenkalkulation ein!
|
Glücksräder
Glücksrad 1 mit drei gleichen Sektoren absolute Häufigkeit
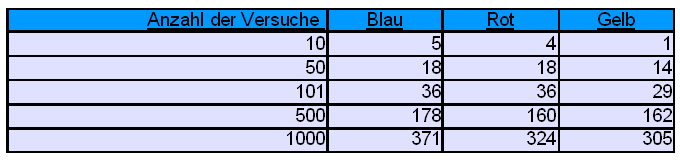
|
Hausaufgabe auf Montag
- Wiederhole, wie man den Prozentanteil (Prozentsatz) berechnet: Übung
- Berechne nun die Prozentsätze der Ergebnisse Deines Versuches nach 10, 50, 100, 500, 1000 Deiner Versuche, trage sie in die zweite Tabelle ein und bringe die ausgefüllte Tabelle am Montag in die Schule mit.
|
Das sind unsere Ergebnisse:
Glücksrad 1: drei gleiche Sektoren
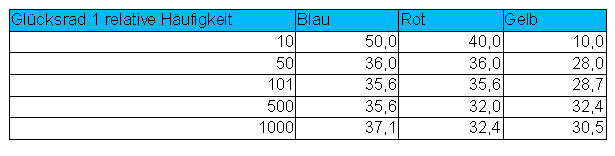
Glücksrad 2: 10 gleiche Sektoren

Wenn Du mit gleichen Glücksrädern experimentierst, dann kannst Du ganz andere relative Häufigkeiten erhalten.
|
Arbeitsaufgaben
1. Was hattest Du für die relative Häufigkeiten der einzelnen Glücksräder erwartet?
2. Stelle nun die relativen Häufigkeiten für Glücksrad 1 und Glücksrad 2 in jeweils einem Digramm dar.
3. Für welche Diagrammform hattest Du Dich entschieden? Betrachte dazu das nächste Bild:
|
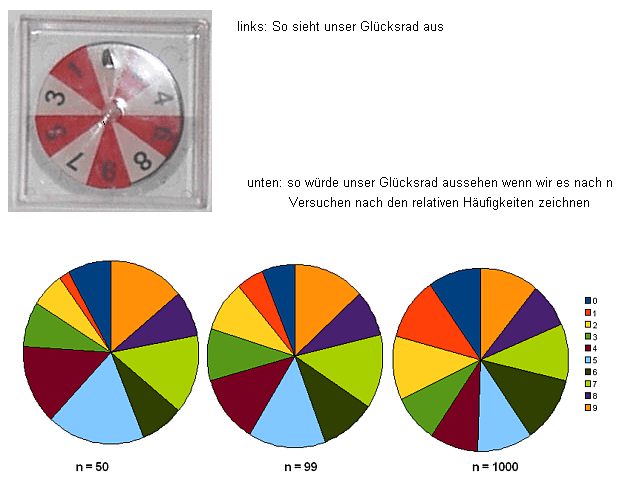
Datei:6d1.jpg
|
Arbeitsaufgaben
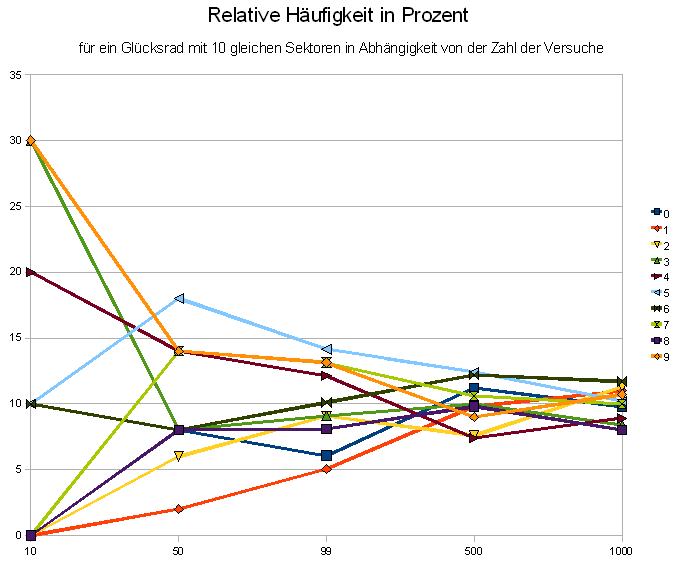
1. Betrachte nun die folgenden zwei Diagramme.
2. Beschreibe das Verhalten der relativen Häufigkeiten bei geringer Zahl der Versuche.
3. Was beobachtest Du bei wachsender Zahl der Versuche.
4. Formuliere Deine Beobachtungen im Heft in zwei Sätzen.
|
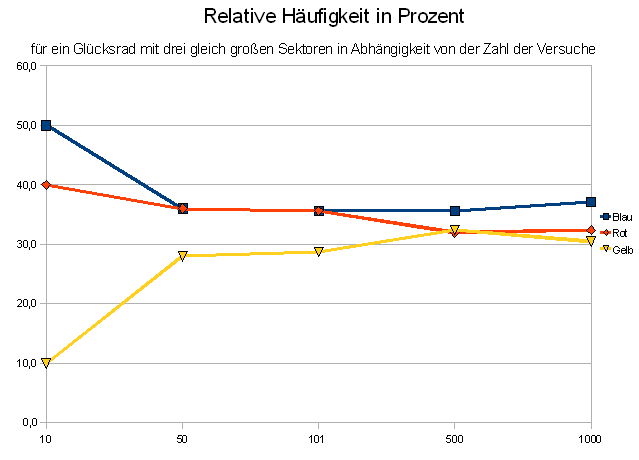
Datei:6d2.jpg
Simulation von Glücksrädern, Würfeln und Münzen
|
|
|
|
|
Arbeitsaufgabe:
Experimentiere mit den Computer-Glücksrädern, Würfeln und Münzen und untersuche, ob Deine Vermutung, die Du in der letzten Arbeitsaufgabe formuliert hast stimmt.
|
Das Gesetz der großen Zahlen
|
|
|
|
|
Das sog. empirische Gesetz der großen Zahlen besagt, dass bei einem Zufallsexperiment die relative Häufigkeit der Ergebnisse des Zufallsexperimentes sich um einen bestimmten Wert stabilisieren.
|
|
|
|
|
Schreibe das Gesetz in Dein Matheheft!
Betrachte dazu noch einmal die beiden letzten Graphiken!
Informiere Dich auch bei Wikipedia über das Gesetz der großen Zahlen!
Hier kannst Du experimentieren: Versuch zum Gesetz der großen Zahlen.
|
Gezinkte Würfel, Münzen - erkennen, nachweisen, aber wie?
|
|
|
|
Von "gezinkten" Würfeln, Münzen oder Glücksrädern spricht man, wenn die relative Häufigkeit mit der ein "Ereignis" eintritt von der erwarteten relativen Häufigkeit abweicht. Also bei genügender Wurfzahl beispielsweise zuviel 1-er fallen.

So einfach ist es nicht immer, gezinkte Karten, Würfel, Münzen oder Glücksräder zu erkennen wie auf dem obigen Bild!
|
Arbeitsaufgaben:
Informiere Dich bei http://de.wikipedia.org/wiki/Münzwurf Wikipedia, bei welchen Ereignissen im „wirklichen Leben“ Münzwürfe Entscheidungen herbeiführen.
Dein Lehrer hat zwei „gleichartige Münzen“ mitgebracht: die Hausaufgabenmünzen. Am Ende der Stunde will er mit einer von ihnen entscheiden, ob es eine schriftliche Hausaufgabe gibt oder nicht.
Wenn „Zahl“ beim Werfen der Münze oben liegt ist Hausaufgabe zu machen. Liegt dagegen „Wappen“ oben, gibt es keine schriftliche Hausaufgabe.
Damit die 6 d aber oft genug eine schriftliche Hausaufgabe machen muss, hat er eine Münze gezinkt.
Überlege dir mit dem Simulator Münzwurf wie Du entscheiden kannst, welche der „Hausaufgabenmünzen“ der Lehrer gezinkt hat, also fast immer das Ergebnis „Schriftliche Hausaufgabe“ anzeigt.
Teste nun die Münzen des Lehrers und entscheide, welche Münze der Lehrer am Ende der Stunde für seine Entscheidung nehmen soll.
Hausaufgabe:
Überlege, was der Lehrer gemacht hat, um die Münze zu zinken.
Bastle eine gezinkte Münze. Dazu kannst Du die Bilder rechts ausdrucken, in dem Du den Mauszeiger auf das Bild setzt und die rechte Maustaste drückst. Speichere das Bild ab und öffne es in einem Graphikprogramm (z.B. Paint) um es auszudrucken.
|

|
</td>
|

Homepage des Aktionstages
Videochannel auf YouTube
Lernmodule bei ZUM.de
Linkdatenbank Mathematik
|













