M8 Ähnliche Dreiecke: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 24: | Zeile 24: | ||
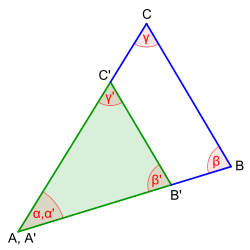
1. Zwei Dreiecke sind zueinander ähnlich, wenn sie in zwei Winkeln übereinstimmen. <br> | 1. Zwei Dreiecke sind zueinander ähnlich, wenn sie in zwei Winkeln übereinstimmen. <br> | ||
| − | <center | + | <center>[[Datei:01-Ähnlichkeitssatz_Dreieck-WWW.svg|200px]]<br> |
| + | Die drei Winkel sind jeweils gleich.</center> | ||
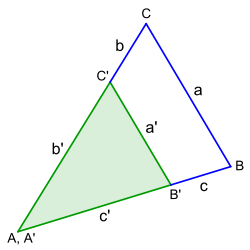
2. Zwei Dreiecke sind zueinander ähnlich, wenn sie in allen Verhältnissen entsprechender Seiten übereinstimmen. <br> | 2. Zwei Dreiecke sind zueinander ähnlich, wenn sie in allen Verhältnissen entsprechender Seiten übereinstimmen. <br> | ||
| − | <center>[[Datei:01-Ähnlichkeitssatz_Dreieck-SSS.svg|200px]]</center> | + | <center>[[Datei:01-Ähnlichkeitssatz_Dreieck-SSS.svg|200px]]<br> |
| + | a : a' = (b + b') : b' = (c + c') : c' </center> | ||
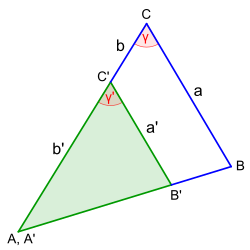
3. Zwei Dreiecke sind zueinander ähnlich, wenn sie in einem Winkel und im Verhältnis der anliegenden Seiten übereinstimmen. <br> | 3. Zwei Dreiecke sind zueinander ähnlich, wenn sie in einem Winkel und im Verhältnis der anliegenden Seiten übereinstimmen. <br> | ||
| − | <center>[[Datei:01-Ähnlichkeitssatz_Dreieck-SWS.svg|200px]]</center> | + | <center>[[Datei:01-Ähnlichkeitssatz_Dreieck-SWS.svg|200px]]<br> |
| + | a : a' = (b + b') : b', γ=γ' (eingeschlossene Winkiel) </center> | ||
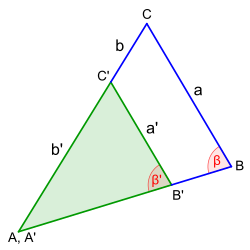
4. Zwei Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis zweier Seiten und im gegenüberliegenden Winkel der größeren Seite übereinstimmen.<br> | 4. Zwei Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis zweier Seiten und im gegenüberliegenden Winkel der größeren Seite übereinstimmen.<br> | ||
| − | <center>[[Datei:01-Ähnlichkeitssatz_Dreieck-SSW.svg|200px]] </center> }} | + | <center>[[Datei:01-Ähnlichkeitssatz_Dreieck-SSW.svg|200px]]<br> |
| + | a : a' = (b + b') : b', β=β' (Winkel, die der jeweils größeren Seite gegenüberliegen) </center> }} | ||
Version vom 7. Juli 2020, 10:14 Uhr
Strahlensatz und Ähnlichkeit
Du kennst die Kongruenzsätze:
sss-Satz (erster Kongruenzsatz)
Zwei Dreiecke sind kongruent, wenn sie in ihren drei Seitenlängen übereinstimmen.
sws-Satz (zweiter Kongruenzsatz)
Zwei Dreiecke sind kongruent, wenn sie in zwei Seitenlängen und in dem eingeschlossenen Winkel übereinstimmen.
wsw-Satz (dritter Kongruenzsatz)
Zwei Dreiecke sind kongruent, wenn sie in einer Seitenlänge und in den dieser Seite anliegenden Winkeln übereinstimmen.
Ssw-Satz (vierter Kongruenzsatz)
Zwei Dreiecke sind kongruent, wenn sie in zwei Seitenlängen und in jenem Winkel übereinstimmen, der der längeren Seite
gegenüberliegt.
Analog dazu gibt es 4 Ähnlichkeitssätze:
|
Meistens wendet man den ersten Ähnlichkeitssatz an. Man schaut ob zwei Dreiecke in zwei Winkeln übereinstimmen! |