M8 Ähnliche Dreiecke: Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
Du kennst die Kongruenzsätze: | Du kennst die Kongruenzsätze: | ||
| − | + | Erster Kongruenzsatz (sss-Satz)<br> | |
| − | + | Zwei Dreiecke sind kongruent, wenn sie in ihren drei Seitenlängen übereinstimmen. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | Zweiter Kongruenzsatz (sws-Satz)<br> | ||
| + | Zwei Dreiecke sind kongruent, wenn sie in zwei Seitenlängen und in dem eingeschlossenen Winkel übereinstimmen. | ||
| − | Analog dazu gibt | + | Dritter Kongruenzsatz (wsw-Satz)<br> |
| + | Zwei Dreiecke sind kongruent, wenn sie in einer Seitenlänge und in den dieser Seite anliegenden Winkeln übereinstimmen. | ||
| + | |||
| + | Vierter Kongruenzsatz (Ssw-Satz)<br> | ||
| + | Zwei Dreiecke sind kongruent, wenn sie in zwei Seitenlängen und in jenem Winkel übereinstimmen, der der längeren Seite gegenüberliegt. | ||
| + | |||
| + | Die Forderung nach Kongruenz ist ziemlich groß. Die Dreiecke sind dann deckungsgleich. <br> | ||
| + | Oftmals schauen aber Dreiecke fast gleich aus, sind es aber nicht, sondern unterscheiden sich in der Größe. Man sagt dann sie sind '''ähnlich'''. | ||
| + | |||
| + | Analog dazu gibt für Dreiecke vier Ähnlichkeitssätze: | ||
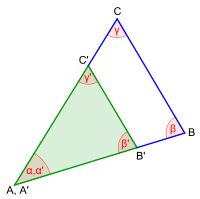
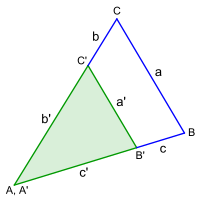
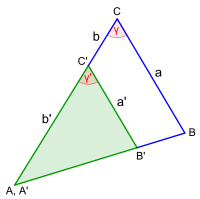
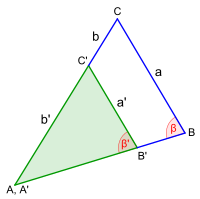
{{Merksatz|MERK=Die vier Ähnlichkeitssätze für Dreiecke lauten: | {{Merksatz|MERK=Die vier Ähnlichkeitssätze für Dreiecke lauten: | ||
| Zeile 37: | Zeile 41: | ||
4. Zwei Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis zweier Seiten und im gegenüberliegenden Winkel der größeren Seite übereinstimmen.<br> | 4. Zwei Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis zweier Seiten und im gegenüberliegenden Winkel der größeren Seite übereinstimmen.<br> | ||
<center>[[Datei:01-Ähnlichkeitssatz_Dreieck-SSW.svg|200px]]<br> | <center>[[Datei:01-Ähnlichkeitssatz_Dreieck-SSW.svg|200px]]<br> | ||
| − | a : a' = (b + b') : b', β=β' (Winkel, die der jeweils größeren Seite gegenüberliegen) </center> | + | a : a' = (b + b') : b', β=β' (Winkel, die der jeweils größeren Seite gegenüberliegen) </center> |
| − | + | Meistens wendet man den ersten Ähnlichkeitssatz an. Man schaut ob zwei Dreiecke in zwei Winkeln übereinstimmen! }} | |
Version vom 7. Juli 2020, 09:20 Uhr
Strahlensatz und Ähnlichkeit
Du kennst die Kongruenzsätze:
Erster Kongruenzsatz (sss-Satz)
Zwei Dreiecke sind kongruent, wenn sie in ihren drei Seitenlängen übereinstimmen.
Zweiter Kongruenzsatz (sws-Satz)
Zwei Dreiecke sind kongruent, wenn sie in zwei Seitenlängen und in dem eingeschlossenen Winkel übereinstimmen.
Dritter Kongruenzsatz (wsw-Satz)
Zwei Dreiecke sind kongruent, wenn sie in einer Seitenlänge und in den dieser Seite anliegenden Winkeln übereinstimmen.
Vierter Kongruenzsatz (Ssw-Satz)
Zwei Dreiecke sind kongruent, wenn sie in zwei Seitenlängen und in jenem Winkel übereinstimmen, der der längeren Seite gegenüberliegt.
Die Forderung nach Kongruenz ist ziemlich groß. Die Dreiecke sind dann deckungsgleich.
Oftmals schauen aber Dreiecke fast gleich aus, sind es aber nicht, sondern unterscheiden sich in der Größe. Man sagt dann sie sind ähnlich.
Analog dazu gibt für Dreiecke vier Ähnlichkeitssätze:
 Merke:
Die vier Ähnlichkeitssätze für Dreiecke lauten: 1. Zwei Dreiecke sind zueinander ähnlich, wenn sie in zwei Winkeln übereinstimmen.  Die drei Winkel sind jeweils gleich. 2. Zwei Dreiecke sind zueinander ähnlich, wenn sie in allen Verhältnissen entsprechender Seiten übereinstimmen.  a : a' = (b + b') : b' = (c + c') : c' 3. Zwei Dreiecke sind zueinander ähnlich, wenn sie in einem Winkel und im Verhältnis der anliegenden Seiten übereinstimmen.  a : a' = (b + b') : b', γ=γ' (eingeschlossene Winkiel) 4. Zwei Dreiecke sind zueinander ähnlich, wenn sie im Verhältnis zweier Seiten und im gegenüberliegenden Winkel der größeren Seite übereinstimmen.  a : a' = (b + b') : b', β=β' (Winkel, die der jeweils größeren Seite gegenüberliegen)
|
