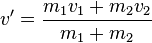Ph10 Impuls und Impulserhaltung: Unterschied zwischen den Versionen
| Zeile 94: | Zeile 94: | ||
{{Lösung versteckt|1=Die Summe der Impulse <math>p_1</math> und <math>p_2</math> vor dem Stoß ist gleich der Summe der Impulse <math>p^'_1</math> und <math>p^'_2</math> nach dem Stoß. Der Gesamtimpuls vor dem Stoß <math>p_1+p_2</math> ist also gleich dem Gesamtimpuls nach dem Stoß <math>p^'_1 + p^'_2</math>.}} | {{Lösung versteckt|1=Die Summe der Impulse <math>p_1</math> und <math>p_2</math> vor dem Stoß ist gleich der Summe der Impulse <math>p^'_1</math> und <math>p^'_2</math> nach dem Stoß. Der Gesamtimpuls vor dem Stoß <math>p_1+p_2</math> ist also gleich dem Gesamtimpuls nach dem Stoß <math>p^'_1 + p^'_2</math>.}} | ||
| − | {{Merksatz|MERK=Für einen zentralen elastischen Stoß | + | {{Merksatz|MERK=Für einen zentralen elastischen Stoß gilt der Impulserhaltungssatz (IES): |
Die Summe der Impule vor dem Stoß ist gleich der Summe der Impule nach dem Stoß. }} | Die Summe der Impule vor dem Stoß ist gleich der Summe der Impule nach dem Stoß. }} | ||
| Zeile 107: | Zeile 107: | ||
Die Geschwindigkeiten <math>v'_1</math> und <math>v'_2</math> der Körper nach dem Stoß erhält man durch die Formeln<br> | Die Geschwindigkeiten <math>v'_1</math> und <math>v'_2</math> der Körper nach dem Stoß erhält man durch die Formeln<br> | ||
<math>v'_1=2\frac{m_1 v_1 + m_2 v_2}{m_+m_2}-v_1</math> und <math>v'_2=2\frac{m_1 v_1 + m_2 v_2}{m_+m_2}-v_2</math> }} | <math>v'_1=2\frac{m_1 v_1 + m_2 v_2}{m_+m_2}-v_1</math> und <math>v'_2=2\frac{m_1 v_1 + m_2 v_2}{m_+m_2}-v_2</math> }} | ||
| + | |||
| + | |||
| + | Als nächstes machen wir das gleiche für den inelastischen Stoß | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
| + | {{Versuch|1=Was passiert mit dem Impuls bei einem Kraftstoß? Dies soll mit dem folgenden Applet untersucht werden.<br> | ||
| + | Öffne das Applet auf der [https://www.walter-fendt.de/html5/phde/collision_de.htm Seite von Walter Fendet]. | ||
| + | |||
| + | Nun wollen wir den inelastischen Stoß untersuchen. Stelle dazu ''unelastischer Stoß'' ein.<br> | ||
| + | Für die zwei Wägen kannst du deren Masse und Anfangsgeschwindigkeit (m1 und v1 für Wagen 1 und m2 und v2 für Wagen2) einstellen.<br> | ||
| + | Stelle als Ausgabe Geschwindigkeit ein.<br> | ||
| + | Den Versuch startest du durch Betätigen des Start-Buttons. <br> | ||
| + | Mache die Einstellungen, notiere was die Einstellungen bedeuten und führe den Versuch aus. Notiere jeweils deine Beobachtungen.<br> | ||
| + | Notiere auch die angezeigten Geschwindigkeiten vor und nach dem Stoß. | ||
| + | |||
| + | 1. m1 = m2 = 0,5 kg und v1 = 0,2m/s, v2 = 0m/s. | ||
| + | |||
| + | {{Lösung versteckt|1=Die Einstellungen bedeuten, dass ein Wagen 1 mit der Geschwindigkeit v1 auf einen ruhenden, gleich schweren Wagen 2 trifft.<br> | ||
| + | Der Wagen 1 trifft auf Wagen 2. Beim Stoß bleibt Wagen 1 stehen und Wagen 2 bewegt sich mit der Geschwindigkeit von Wagen 1 weiter. }} | ||
| + | |||
| + | 2. m1 = 1kg, m2 = 0,5kg, v1 = 0,2m/s, v2 = 0m/s | ||
| + | |||
| + | {{Lösung versteckt|1=Der Wagen 1 trifft mit der Geschwindigkeit v1 auf einen ruhenden, halb so schweren Wagen 2. <br> | ||
| + | Der Wagen 1 trifft auf Wagen 2 und stößt diesem an. Wagen 2 bewegt sich mit schnellerer Geschwindigkeit als 0,2m/s nach rechts, Wagen 1 rollt mit langsamerer Geschwindigkeit als 0,2m/s auch nach rechts.}} | ||
| + | |||
| + | 3. m1 = 0,5kg, m2 = 1,0kg, v1 = 0,2m/s, v2 = 0m/s | ||
| + | |||
| + | {{Lösung versteckt|1=Der Wagen 1 trifft mit der Geschwindigkeit v1 auf einen ruhenden, doppelt so schweren Wagen 2.<br> | ||
| + | Der Wagen 1 trifft auf den Wagen 2 und stößt diesen an. Wagen 2 bewegt sich mit langsamerer Geschwindigkeit als 0,2m/s nach rechts, Wagen 1 rollt mit langsamerer Geschwindigkeit als 0,2m/2 zurück nach links.}} | ||
| + | |||
| + | 4. Mache nun selbst Änderungen für v1 und schau was sich beim Versuch mit sonst gleichen Einstellungen wie 1. - 3. ändert. | ||
| + | |||
| + | {{Lösung versteckt|1=Es ergeben sich analoge Ergebnisse.}} | ||
| + | |||
| + | 5. m1 = m2 = 0,5 kg und v1 = 0,2m/s, v2 = -0,2m/s. | ||
| + | |||
| + | {{Lösung versteckt|1=Die gleich schweren Wägen 1 und 2 fahren in entgegengesetzte Richtung. Wagen 1 fährt nach rechts, Wagen 2 nach links.<br> | ||
| + | Die Wägen fahren aufeinander zu und stoßen zusammen. Wagen 1 fährt danach mit der Geschwindigkeit -0,2m/s nach links und Wagen 2 fährt mit der Geschwindigkeit 0,2m/s nach rechts. Der Betrag ihrer Geschwindigkeiten ändert sich nicht, die Wägen ändern jeweils ihre Bewegungsrichtung. }} | ||
| + | |||
| + | 6. m1 = 1kg, m2 = 0,5kg, v1 = 0,2m/s, v2 = -0,2m/s | ||
| + | |||
| + | {{Lösung versteckt|1=Der doppelt so schwere Wagen 1 fährt gegen den entgegen kommenden Wagen 2. | ||
| + | Nach dem Stoß fahren beide Wägen wieder auseinander. Wagen 1 fährt langsamer als 0,2m/s nach links, Wagen 2 fährt schneller als 0,2m/s nach rechts.}} | ||
| + | |||
| + | 7. m1 = 0,5kg, m2 = 1kg, v1 = 0,2m/s, v2 = -0,2m/s | ||
| + | |||
| + | {{Lösung versteckt|1=Der halb so schwere Wagen 1 fährt gegen den entgegen kommenden Wagen 2. | ||
| + | Nach dem Stoß fahren beide Wägen wieder auseinander. Wagen 1 fährt schneller als 0,2m/s nach links, Wagen 2 fährt langsamer als 0,2m/s nach rechts. (Wie 6. nur mit gewechselten Rollen von Wagen 1 und 2.)}} | ||
| + | }} | ||
| + | |||
| + | |||
| + | Für die Wechselwirkung der beiden Wägen trifft das 3. Newtonsche Gesetz zu:<br> | ||
| + | <center> <math> F_{12} = - F_{21}</math></center> | ||
| + | , dabei ist <math>F_{12}</math> die Kraft die Wagen 2 auf Wagen 1 und <math>F_{21}</math> die Kraft die Wagen 1 auf Wagen 2 ausübt. Die beiden Kräfte sind gleich groß, aber entgegengesetzt gerichtet. Die Richtung wird durch - ausgedrückt. | ||
| + | |||
| + | Die Kräfte bewirken jeweils eine Beschleunigung der Wägen: | ||
| + | <center> <math>F_{12} = - F_{21}</math></center> | ||
| + | <center> <math>m_1 \cdot a_1 = - m_2 \cdot a_2</math></center> | ||
| + | Die Beschleunigung <math>a</math> bewirkt jeweils eine Geschwindigkeitsänderung <math>\Delta v</math>. Es ist <math>a = \frac{\Delta v}{\Delta t}</math> und damit | ||
| + | <center> <math>m_1 \cdot \frac{\Delta v_1}{\Delta t} = - m_2 \cdot \frac{\Delta v_2}{\Delta t}</math></center> | ||
| + | Bezeichnen <math>v_1</math> und <math>v_2</math> die Geschwindigkeiten von Wagen 1 und Wagen 2 vor dem Stoß und <math>v^'_1</math> und <math>v^'_2</math> die Geschwindigkeiten von Wagen 1 und Wagen 2 nach dem Stoß, so ist <math>\Delta v_1 = v^'_1 - v_1</math> und <math>\Delta v_2=v^'_2 - v_2</math>. | ||
| + | Damit | ||
| + | <center> <math>m_1 \cdot \frac{v^'_1 - v_1}{\Delta t} = - m_2 \cdot \frac{ v^'_2 - v_2}{\Delta t}</math></center> | ||
| + | Multipliziert man die Gleichung mit <math>\Delta t</math>, so erhält man | ||
| + | <center> <math>m_1 \cdot (v^'_1 - v_1) = - m_2 \cdot (v^'_2 - v_2)</math></center> | ||
| + | oder | ||
| + | <center><math> m_1 v^'_1 - m_1 v_1 = - m_2 v^'_2 + m_2 v_2</math></center> | ||
| + | Bringt man die v-Terme auf die linke Seite und die u-Terme auf die rechte Seite, so ergibt sich: | ||
| + | <center><math> - m_1 v_1 - m_2 v_2 = -m_1 v^'_1 - m_2 v^'_2</math></center> | ||
| + | Nun multipliziert man die Gleichung mit -1 | ||
| + | <center><math> m_1 v_1 + m_2 v_2 = m_1 v^'_1 + m_2 v^'_2</math></center> | ||
| + | |||
| + | Verwendet man nun für das Produkt <math>m v</math> den Impuls <math>p</math>, erhält man | ||
| + | <center><math>p_1 + p_2 = p^'_1 + p^'_2</math></center> | ||
| + | |||
| + | |||
| + | {{Merke|1=Beim inelastischen Stoß zweier Körper 1 und 2 gilt für ihre Impulse <math>p_1</math> und <math>p_2</math> vor dem Stoß und <math>p^'_1</math> und <math>p^'_2</math> nach dem Stoß. | ||
| + | |||
| + | <center><math>p_1 + p_2 = p^'_1 + p^'_2</math></center> | ||
| + | }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Formuliere die Aussage des Merksatzes in einem Satz.}} | ||
| + | |||
| + | {{Lösung versteckt|1=Die Summe der Impulse <math>p_1</math> und <math>p_2</math> vor dem Stoß ist gleich der Summe der Impulse <math>p^'_1</math> und <math>p^'_2</math> nach dem Stoß. Der Gesamtimpuls vor dem Stoß <math>p_1+p_2</math> ist also gleich dem Gesamtimpuls nach dem Stoß <math>p^'_1 + p^'_2</math>.}} | ||
| + | |||
| + | {{Merksatz|MERK=Für einen zentralen elastischen Stoß gilt der Impulserhaltungssatz (IES): | ||
| + | |||
| + | Die Summe der Impule vor dem Stoß ist gleich der Summe der Impule nach dem Stoß. }} | ||
| + | |||
| + | {{Aufgaben-blau|4|2=Schaue dir diesen Video an und fasse die Aussagen zusammen. | ||
| + | <center>{{#ev:youtube |KDeTMewYSyg|350}}</center> }} | ||
| + | |||
| + | {{Lösung versteckt|Beim inelastischen Stoß gilt nicht der Energieerhaltungssatz für die Bewegungsenergie. Bewegungsenergie wird in Verformungsenergie und Wärme umgewandelt. Der Impulserhaltungssatz (IES) gilt.<br> | ||
| + | Man kann den EES aber trotzdem in der Art <br> | ||
| + | EES: <math>\frac{1}{2} m_1 v_1 ^2-\frac{1}{2} m_2 v_2 ^2= \frac{1}{2} m_1 v_1' ^2+\frac{1}{2} m_2 v_2' ^2 + \Delta W</math> , wobei <math> \Delta W</math> die Wärme und Verformungsenergie ist. <br> | ||
| + | Beim inelastischen Stoß bewegen sich die beiden Körper nach dem Stoß zusammen fort, sie haben also eine gemeinsame Geschwindigkeit <math>v'</math>. <br> | ||
| + | EES: <math>\frac{1}{2} m_1 v_1 ^2-\frac{1}{2} m_2 v_2 ^2= \frac{1}{2} (m_1+m_2) v' ^2 + \Delta W</math><br> | ||
| + | IES: <math>m_1 v_1 + m_2 v_2 = (m_1+m_2) v' </math><br> | ||
| + | |||
| + | Die Geschwindigkeiten <math>v'</math> der beiden Körper nach dem Stoß erhält man aus dem IES <br> | ||
| + | <math>v'=\frac{m_1 v_1 + m_2 v_2}{m_1+m_2}</math> }} | ||
Version vom 20. November 2020, 16:55 Uhr
30px Versuch
Was passiert mit dem Impuls bei einem Kraftstoß? Dies soll mit dem folgenden Applet untersucht werden. a) Schaue dir zuerst die Seite an, was kannst du einstellen?
a) Man kann einstellen: b) Bei einem elastischen Stoß stoßen zwei Körper aufeinander, dabei wird keine Energie in innere Energie umgewandelt.
1. m1 = m2 = 0,5 kg und v1 = 0,2m/s, v2 = 0m/s.
Die Einstellungen bedeuten, dass ein Wagen 1 mit der Geschwindigkeit v1 auf einen ruhenden, gleich schweren Wagen 2 trifft. 2. m1 = 1kg, m2 = 0,5kg, v1 = 0,2m/s, v2 = 0m/s
Der Wagen 1 trifft mit der Geschwindigkeit v1 auf einen ruhenden, halb so schweren Wagen 2. 3. m1 = 0,5kg, m2 = 1,0kg, v1 = 0,2m/s, v2 = 0m/s
Der Wagen 1 trifft mit der Geschwindigkeit v1 auf einen ruhenden, doppelt so schweren Wagen 2. 4. Mache nun selbst Änderungen für v1 und schau was sich beim Versuch mit sonst gleichen Einstellungen wie 1. - 3. ändert.
Es ergeben sich analoge Ergebnisse.
5. m1 = m2 = 0,5 kg und v1 = 0,2m/s, v2 = -0,2m/s.
Die gleich schweren Wägen 1 und 2 fahren in entgegengesetzte Richtung. Wagen 1 fährt nach rechts, Wagen 2 nach links. 6. m1 = 1kg, m2 = 0,5kg, v1 = 0,2m/s, v2 = -0,2m/s
Der doppelt so schwere Wagen 1 fährt gegen den entgegen kommenden Wagen 2. Nach dem Stoß fahren beide Wägen wieder auseinander. Wagen 1 fährt langsamer als 0,2m/s nach links, Wagen 2 fährt schneller als 0,2m/s nach rechts.7. m1 = 0,5kg, m2 = 1kg, v1 = 0,2m/s, v2 = -0,2m/s
Der halb so schwere Wagen 1 fährt gegen den entgegen kommenden Wagen 2. Nach dem Stoß fahren beide Wägen wieder auseinander. Wagen 1 fährt schneller als 0,2m/s nach links, Wagen 2 fährt langsamer als 0,2m/s nach rechts. (Wie 6. nur mit gewechselten Rollen von Wagen 1 und 2.) |
Für die Wechselwirkung der beiden Wägen trifft das 3. Newtonsche Gesetz zu:
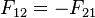
, dabei ist 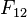 die Kraft die Wagen 2 auf Wagen 1 und
die Kraft die Wagen 2 auf Wagen 1 und 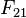 die Kraft die Wagen 1 auf Wagen 2 ausübt. Die beiden Kräfte sind gleich groß, aber entgegengesetzt gerichtet. Die Richtung wird durch - ausgedrückt.
die Kraft die Wagen 1 auf Wagen 2 ausübt. Die beiden Kräfte sind gleich groß, aber entgegengesetzt gerichtet. Die Richtung wird durch - ausgedrückt.
Die Kräfte bewirken jeweils eine Beschleunigung der Wägen:
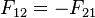
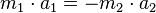
Die Beschleunigung 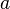 bewirkt jeweils eine Geschwindigkeitsänderung
bewirkt jeweils eine Geschwindigkeitsänderung 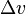 . Es ist
. Es ist 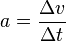 und damit
und damit
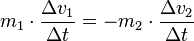
Bezeichnen 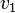 und
und 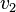 die Geschwindigkeiten von Wagen 1 und Wagen 2 vor dem Stoß und
die Geschwindigkeiten von Wagen 1 und Wagen 2 vor dem Stoß und 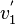 und
und 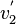 die Geschwindigkeiten von Wagen 1 und Wagen 2 nach dem Stoß, so ist
die Geschwindigkeiten von Wagen 1 und Wagen 2 nach dem Stoß, so ist 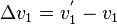 und
und 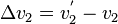 .
Damit
.
Damit
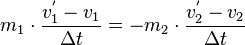
Multipliziert man die Gleichung mit 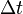 , so erhält man
, so erhält man
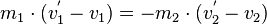
oder
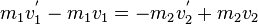
Bringt man die v-Terme auf die linke Seite und die u-Terme auf die rechte Seite, so ergibt sich:
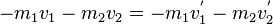
Nun multipliziert man die Gleichung mit -1
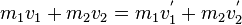
Verwendet man nun für das Produkt 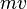 den Impuls
den Impuls 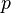 , erhält man
, erhält man
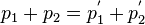
30px Merke
Beim elastischen Stoß zweier Körper 1 und 2 gilt für ihre Impulse 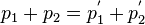 |
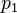 und
und 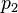 vor dem Stoß ist gleich der Summe der Impulse
vor dem Stoß ist gleich der Summe der Impulse 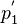 und
und 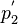 nach dem Stoß. Der Gesamtimpuls vor dem Stoß
nach dem Stoß. Der Gesamtimpuls vor dem Stoß 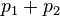 ist also gleich dem Gesamtimpuls nach dem Stoß
ist also gleich dem Gesamtimpuls nach dem Stoß 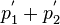 .
.|
Merke:
Für einen zentralen elastischen Stoß gilt der Impulserhaltungssatz (IES): Die Summe der Impule vor dem Stoß ist gleich der Summe der Impule nach dem Stoß. |
Beim elastischen Stoß gelten der Energieerhaltungssatz (EES) und Impulserhaltungssatz (IES).
EES: 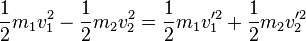
IES: 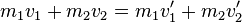
Die Geschwindigkeiten 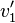 und
und 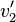 der Körper nach dem Stoß erhält man durch die Formeln
der Körper nach dem Stoß erhält man durch die Formeln
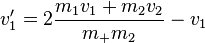 und
und 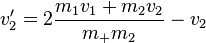
Als nächstes machen wir das gleiche für den inelastischen Stoß
30px Versuch
Was passiert mit dem Impuls bei einem Kraftstoß? Dies soll mit dem folgenden Applet untersucht werden. Nun wollen wir den inelastischen Stoß untersuchen. Stelle dazu unelastischer Stoß ein. 1. m1 = m2 = 0,5 kg und v1 = 0,2m/s, v2 = 0m/s.
Die Einstellungen bedeuten, dass ein Wagen 1 mit der Geschwindigkeit v1 auf einen ruhenden, gleich schweren Wagen 2 trifft. 2. m1 = 1kg, m2 = 0,5kg, v1 = 0,2m/s, v2 = 0m/s
Der Wagen 1 trifft mit der Geschwindigkeit v1 auf einen ruhenden, halb so schweren Wagen 2. 3. m1 = 0,5kg, m2 = 1,0kg, v1 = 0,2m/s, v2 = 0m/s
Der Wagen 1 trifft mit der Geschwindigkeit v1 auf einen ruhenden, doppelt so schweren Wagen 2. 4. Mache nun selbst Änderungen für v1 und schau was sich beim Versuch mit sonst gleichen Einstellungen wie 1. - 3. ändert.
Es ergeben sich analoge Ergebnisse.
5. m1 = m2 = 0,5 kg und v1 = 0,2m/s, v2 = -0,2m/s.
Die gleich schweren Wägen 1 und 2 fahren in entgegengesetzte Richtung. Wagen 1 fährt nach rechts, Wagen 2 nach links. 6. m1 = 1kg, m2 = 0,5kg, v1 = 0,2m/s, v2 = -0,2m/s
Der doppelt so schwere Wagen 1 fährt gegen den entgegen kommenden Wagen 2. Nach dem Stoß fahren beide Wägen wieder auseinander. Wagen 1 fährt langsamer als 0,2m/s nach links, Wagen 2 fährt schneller als 0,2m/s nach rechts.7. m1 = 0,5kg, m2 = 1kg, v1 = 0,2m/s, v2 = -0,2m/s
Der halb so schwere Wagen 1 fährt gegen den entgegen kommenden Wagen 2. Nach dem Stoß fahren beide Wägen wieder auseinander. Wagen 1 fährt schneller als 0,2m/s nach links, Wagen 2 fährt langsamer als 0,2m/s nach rechts. (Wie 6. nur mit gewechselten Rollen von Wagen 1 und 2.) |
Für die Wechselwirkung der beiden Wägen trifft das 3. Newtonsche Gesetz zu:
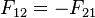
, dabei ist 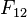 die Kraft die Wagen 2 auf Wagen 1 und
die Kraft die Wagen 2 auf Wagen 1 und 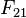 die Kraft die Wagen 1 auf Wagen 2 ausübt. Die beiden Kräfte sind gleich groß, aber entgegengesetzt gerichtet. Die Richtung wird durch - ausgedrückt.
die Kraft die Wagen 1 auf Wagen 2 ausübt. Die beiden Kräfte sind gleich groß, aber entgegengesetzt gerichtet. Die Richtung wird durch - ausgedrückt.
Die Kräfte bewirken jeweils eine Beschleunigung der Wägen:
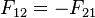
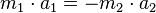
Die Beschleunigung 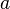 bewirkt jeweils eine Geschwindigkeitsänderung
bewirkt jeweils eine Geschwindigkeitsänderung 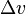 . Es ist
. Es ist 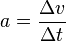 und damit
und damit
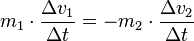
Bezeichnen 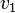 und
und 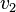 die Geschwindigkeiten von Wagen 1 und Wagen 2 vor dem Stoß und
die Geschwindigkeiten von Wagen 1 und Wagen 2 vor dem Stoß und 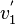 und
und 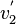 die Geschwindigkeiten von Wagen 1 und Wagen 2 nach dem Stoß, so ist
die Geschwindigkeiten von Wagen 1 und Wagen 2 nach dem Stoß, so ist 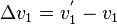 und
und 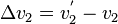 .
Damit
.
Damit
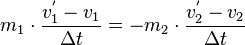
Multipliziert man die Gleichung mit 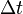 , so erhält man
, so erhält man
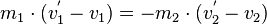
oder
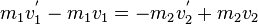
Bringt man die v-Terme auf die linke Seite und die u-Terme auf die rechte Seite, so ergibt sich:
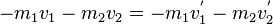
Nun multipliziert man die Gleichung mit -1
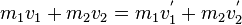
Verwendet man nun für das Produkt 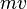 den Impuls
den Impuls 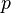 , erhält man
, erhält man
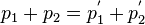
30px Merke
Beim inelastischen Stoß zweier Körper 1 und 2 gilt für ihre Impulse 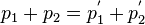 |
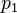 und
und 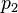 vor dem Stoß ist gleich der Summe der Impulse
vor dem Stoß ist gleich der Summe der Impulse 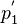 und
und 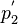 nach dem Stoß. Der Gesamtimpuls vor dem Stoß
nach dem Stoß. Der Gesamtimpuls vor dem Stoß 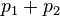 ist also gleich dem Gesamtimpuls nach dem Stoß
ist also gleich dem Gesamtimpuls nach dem Stoß 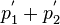 .
.|
Merke:
Für einen zentralen elastischen Stoß gilt der Impulserhaltungssatz (IES): Die Summe der Impule vor dem Stoß ist gleich der Summe der Impule nach dem Stoß. |
Beim inelastischen Stoß gilt nicht der Energieerhaltungssatz für die Bewegungsenergie. Bewegungsenergie wird in Verformungsenergie und Wärme umgewandelt. Der Impulserhaltungssatz (IES) gilt.
Man kann den EES aber trotzdem in der Art
EES: 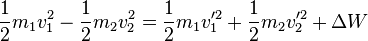 , wobei
, wobei 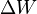 die Wärme und Verformungsenergie ist.
die Wärme und Verformungsenergie ist.
Beim inelastischen Stoß bewegen sich die beiden Körper nach dem Stoß zusammen fort, sie haben also eine gemeinsame Geschwindigkeit 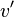 .
.
EES: 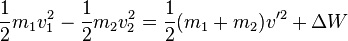
IES: 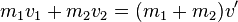
Die Geschwindigkeiten 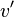 der beiden Körper nach dem Stoß erhält man aus dem IES
der beiden Körper nach dem Stoß erhält man aus dem IES