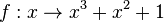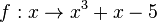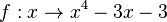M11 Das Newtonsche Iterationsverfahren: Unterschied zwischen den Versionen
| Zeile 30: | Zeile 30: | ||
a) <math>f:x \rightarrow x^3+x^2+1</math><br> | a) <math>f:x \rightarrow x^3+x^2+1</math><br> | ||
b) <math>f:x \rightarrow x^3+x-5</math><br> | b) <math>f:x \rightarrow x^3+x-5</math><br> | ||
| − | c) <math>f:x \rightarrow x^4-3x-3</math><br>}} | + | c) <math>f:x \rightarrow x^4-3x-3</math><br> |
| + | |||
| + | In der Tabellenkalukaltion können Sie leicht den Startwert x<sub>0</sub> ändern. Variieren Sie x<sub>0</sub> und schauen Sie nach wie vielen Schritten Sie die Nullstelle erhalten.}} | ||
{{Lösung versteckt|1=a) x<sub>26</sub> = - 1,46557<br> | {{Lösung versteckt|1=a) x<sub>26</sub> = - 1,46557<br> | ||
b) x<sub>6</sub> = 1,51598<br> | b) x<sub>6</sub> = 1,51598<br> | ||
c) x<sub>7</sub> = 1,6846 }} | c) x<sub>7</sub> = 1,6846 }} | ||
| + | |||
| + | {{Aufgaben-blau|4|2=Bearbeiten Sie im Buch S. 84/10 }} | ||
Version vom 11. Dezember 2020, 08:59 Uhr
Für lineare und quadratische Funktionen hat man zur Bestimmung der Nullstellen Gleichungen zu lösen. Bei quadratischen Funktionen gibt es hierzu die Lösungsformel. Für Polynome höheren Grades kann man meist nur Nullstellen erraten und dann per Polynomdivision versuchen auf ein Polynom 2. Grades zu kommen.
Bei vielen Funktionen hat man Probleme die Nullstellen zu bestimmen. Oftmals reicht es aus, wenn man einen Näherungswert hat. Ein Verfahren um einen Näherungswert für die Nullstelle einer Funktion zu finden ist das Newtonsche Iterationsverfahren.
a) x1 = 3,2235
Diese Lösung soll nochmals ausführlich dargestellt werden. Man erhält x1 indem man im Punkt P(x0),f(x0) auf dem Graphen von f die Tangente macht.
Es ist f(5) = 53+52+1=151.
Die Steigung der Tangente erhält man durch f'(5).
Die Ableitungsfunktion f' ist durch f(x) = 3x2+2x gegeben. Es ist f'(5) = 85.
Den Schnittpunkt der Tangente mit der x-Achse ist nun x1 und x1 erhält man nun durch die Formel 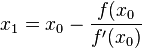 .
.
Es ist also 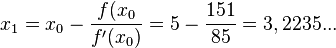
b) x1 = 3,3552
a) x26 = - 1,46557
b) x6 = 1,51598