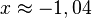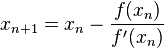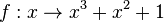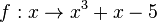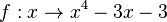M11 Das Newtonsche Iterationsverfahren: Unterschied zwischen den Versionen
| (14 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
In diesem [https://www.geogebra.org/m/sKQqtWq3 Applet] wird das Verfahren schrittweise dargestellt. }} | In diesem [https://www.geogebra.org/m/sKQqtWq3 Applet] wird das Verfahren schrittweise dargestellt. }} | ||
| + | |||
| + | {{Merke|1=Newtonsche Iterationsformel <math>x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}</math> | ||
| + | |||
| + | Diese Formel steht auch in der [http://www.isb.bayern.de/download/13107/merkhilfe_fuer_das_fach_mathematik_standard.pdf Merkhilfe] }} | ||
{{Aufgaben-blau|2|2=Machen Sie jeweils den ersten Schritt des Newton-Verfahrens für die Funktionen<br> | {{Aufgaben-blau|2|2=Machen Sie jeweils den ersten Schritt des Newton-Verfahrens für die Funktionen<br> | ||
| Zeile 21: | Zeile 25: | ||
Die Ableitungsfunktion f' ist durch f(x) = 3x<sup>2</sup>+2x gegeben. Es ist f'(5) = 85. <br> | Die Ableitungsfunktion f' ist durch f(x) = 3x<sup>2</sup>+2x gegeben. Es ist f'(5) = 85. <br> | ||
Den Schnittpunkt der Tangente mit der x-Achse ist nun x<sub>1</sub> und x<sub>1</sub> erhält man nun durch die Formel <math>x_1=x_0-\frac{f(x_0}{f'(x_0)}</math> . <br> | Den Schnittpunkt der Tangente mit der x-Achse ist nun x<sub>1</sub> und x<sub>1</sub> erhält man nun durch die Formel <math>x_1=x_0-\frac{f(x_0}{f'(x_0)}</math> . <br> | ||
| − | Es ist also <math>x_1=x_0-\frac{f(x_0}{f'(x_0)}=5-\frac{151}{85}=3,2235...</math><br> | + | Es ist also <math>x_1=x_0-\frac{f(x_0)}{f'(x_0)}=5-\frac{151}{85}=3,2235...</math><br> |
b) x<sub>1</sub> = 3,3552<br> | b) x<sub>1</sub> = 3,3552<br> | ||
c) x<sub>1</sub> = 3,77876 }} | c) x<sub>1</sub> = 3,77876 }} | ||
| Zeile 38: | Zeile 42: | ||
c) x<sub>7</sub> = 1,6846 }} | c) x<sub>7</sub> = 1,6846 }} | ||
| − | {{Aufgaben-blau|4|2=Bearbeiten Sie im Buch S. 84/10 }} | + | {{Aufgaben-blau|4|2=Bearbeiten Sie im Buch S. 84/10 und 84/11}} |
| + | |||
| + | {{Lösung versteckt|1=84/10 Da <math>x^2+1 \ge 1 > 0</math> ist hat f keine Definitionslücken und auch keine Polstellen.<br> | ||
| + | x = 1 ist doppelte Nullstelle. <br> | ||
| + | Der Grenzwert für <math>x \rightarrow \infty</math> ist wegen Zählergrad = Nennergrad gleich 2 und die waagrechte Asymptote y = 2. <br> | ||
| + | <math>f'(x)=\frac{4(x^2-1)}{(x^2+1)^2}</math><br> | ||
| + | <math>f'(x)=0</math> für x = -1 oder x = 1. Wegen VZW +/- ist bei (-1;4) ein HP und wegen VZW -/+ ist bei (1;0) ein TP.<br> | ||
| + | [[Datei:84-10.jpg]]<br> | ||
| + | Der Flächeninhalt des Rechtecks ist A<sub>R</sub> = 8 und des Quadrats ist A<sub>Q</sub> = 10, also ist A<sub>Q</sub> umd 25% größer als A<sub>R</sub>. | ||
| + | |||
| + | |||
| + | 84/11 <math>f: x \rightarrow \frac{1}{4}x^4-\frac{4}{3}x^3+2x^2</math><br> | ||
| + | G<sub>f</sub> hat Schnittpunkt mit der y-Achse (0;0), da f(0)=0 ist und <br> | ||
| + | Schnittpunkt mit der x-Achse (0;0), da <math>\frac{1}{4}x^4-\frac{4}{3}x^3+2x^2=0</math><br> | ||
| + | <math>x^2(\frac{1}{4}x^2-\frac{4}{3}x+2)=0</math><br><br> | ||
| + | Ein Produkt ist 0, wenn ein Faktor 0 ist, also <math>x=0</math> oder <math>\frac{1}{4}x^2-\frac{4}{3}x+2=0</math>. | ||
| + | Die quadratische Gleichung hat keine Lösung, da ihre Diskriminante <math>D=\left ( \frac{4}{3} \right )^2-4\cdot \frac{1}{4} \cdot 2=\frac{16}{9}-2 <0</math><br> | ||
| + | Also ist x=0 doppelte Nullstelle.<br> | ||
| + | Für die Monotonietabelle braucht man <math>f'</math>. Es ist <math>f'(x)=x^3-4x^2+4x=x(x-2)^2</math><br> | ||
| + | <math>f'(x)=0</math> für <math> x_1=0 , x_2=2</math>, wobei x<sub>2</sub>=2 zweifach ist.<br> | ||
| + | G<sub>f'</sub> ist der Graph eines Polynoms 3. Grades mit Nullstelle bei x<sub>1</sub>=0 und x<sub>2</sub>=2 (doppelt), also hat man bei x<sub>2</sub>=2 keinen Vorzeichenwechsel. <br> | ||
| + | Monotonietabelle:<br> | ||
| + | Für x < 0 ist f'(x) < 0 und G<sub>f</sub> ist streng monoton fallend.<br> | ||
| + | Für x = 0 ist f'(0) = 0 und (0;0) ist wegen VZW -/+ ein TP.<br> | ||
| + | Für 0 < x < 2 ist f'(x) > 0 und G<sub>f</sub> ist streng monoton steigend.<br> | ||
| + | Für x = 2 ist f'(2) = 0 und G<sub>f</sub> hat dort einen Terrassenpunkt, da kein VZW.<br> | ||
| + | Für x > 0 ist f'(x) > 0 und G<sub>f</sub> ist streng monoton steigend. | ||
| + | |||
| + | [[Datei:84-11.jpg|350px]]}} | ||
| + | |||
| + | {{Aufgaben-blau|5|2=Bestimmen Sie näherungsweise die x-Werte der Schnittpunkte der Geraden y = 4 mit dem dem Graphen der Funktion <math>f: x \rightarrow \frac{1}{4}x^4-\frac{4}{3}x^3+2x^2</math>}} | ||
| + | |||
| + | {{Lösung versteckt|1=Für den letzten Teil der Aufgabe 84/11 geht es darum die x-Koordinaten der Punkte A und B zu bestimmen, eigentlich nur dei x-Koordinate von B. | ||
| + | |||
| + | [[Datei:84-11 2.jpg|250px]] | ||
| + | |||
| + | Man muss also x so finden, dass die Gleichung <math>f(x)=4</math> erfüllt ist. Es ist also die Gleichung <br> | ||
| + | <center><math>\frac{1}{4}x^4-\frac{4}{3}x^3+2x^2=4</math></center> | ||
| + | zu lösen, was gleichbedeutend ist Nullstellen der Funktion <math>g</math> mit <math>g(x) =\frac{1}{4}x^4-\frac{4}{3}x^3+2x^2-4</math> zu finden. Man muss also die Gleichung | ||
| + | <center><math>\frac{1}{4}x^4-\frac{4}{3}x^3+2x^2-4=0</math> </center> | ||
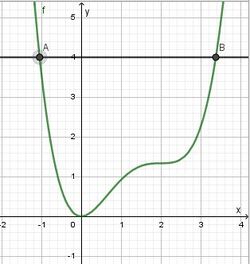
| + | lösen. Hierfür gibt es keine Lösungsformel und das Rezept vom letzten Jahr, dass man eine Nullstelle "rät" und dann Polynomdivision macht geht hier auch nicht. Also bleibt nur das Newton-Verfahren übrig. | ||
| + | |||
| + | [[Datei:84-11 3.jpg|250px]] | ||
| + | |||
| + | Es geht also darum die x-Koordinaten der Punkte D und E zu bestimmen. | ||
| + | Für das Newton-Verfahren hängt es stark ab welchen Startwert x<sub>0</sub> man nimmt. Wir probieren es mit x<sub>0</sub> = 1.<br> | ||
| + | Mit <math>x_0=1</math> ist <math>f(1)=-\frac{37}{12}</math>, <math>f'(x)=1</math> und <math>x_1=x_0-\frac{f(1)}{f'(1)}=1-\frac{-\frac{37}{12}}{1}=\frac{49}{12} \approx 4,0833</math><br> | ||
| + | Es ist dann <math>f(\frac{49}{12})\approx 8,08100</math> und <math>f'(\frac{49}{12})=17,7228</math> und <math>x_2=x_1-\frac{f(x_1)}{f'(x_1)}=4,0833-\frac{8,0810}{17,7228}\approx 3,6979</math><br> | ||
| + | Im Graph schaut das so aus:<br> | ||
| + | [[Datei:84-11 4.jpg|350px]] | ||
| + | Es geht weiter mit <math>f(x_2)\approx 1,9654</math> und <math>f'(x_2)\approx 9,6146</math> und <math>x_3=3,6979-\frac{1,9654}{9,6146}=3,4235</math> und<br> | ||
| + | <math>f(x_3)\approx 0,2830</math> und <math>f'(x_3)\approx 6,9374</math> und <math>x_4=3,4235-\frac{0,2830}{6,9374}=3,3827</math> und<br> | ||
| + | <math>f(x_4)\approx 0,00965</math> und <math>f'(x_4)\approx 6,4675</math> und <math>x_5=3,3827-\frac{0,00965}{6,4675}=3,3812</math> <br> | ||
| + | Damit ändert sich auf zwei Nachkommastellen die Nullstelle nicht mehr, es ist also <math> x \approx 3,38</math> | ||
| + | |||
| + | Mit einer Tabellenkalkulation geht es natürlich viel schneller und übersichtlicher.<br> | ||
| + | Das schöne dabei ist, dass man den Startwert leicht ändern und in einer Tabelle die Annäherung an die Nullstelle gut nachvollziehen kann. <br> | ||
| + | Wieso geht <<sub>0</sub> = 2 nicht als Startwert?<br> | ||
| + | Bei Startwerten x<sub>0</sub> > 1 kommt man stets zu unserer Nullstelle <math> x \approx 3,38</math>.<br> | ||
| + | Beim Startwert x<sub>0</sub>> = -2 kommt man zur anderen Nullstelle <math> x \approx -1,04</math> }} | ||
Aktuelle Version vom 15. Dezember 2020, 18:55 Uhr
Für lineare und quadratische Funktionen hat man zur Bestimmung der Nullstellen Gleichungen zu lösen. Bei quadratischen Funktionen gibt es hierzu die Lösungsformel. Für Polynome höheren Grades kann man meist nur Nullstellen erraten und dann per Polynomdivision versuchen auf ein Polynom 2. Grades zu kommen.
Bei vielen Funktionen hat man Probleme die Nullstellen zu bestimmen. Oftmals reicht es aus, wenn man einen Näherungswert hat. Ein Verfahren um einen Näherungswert für die Nullstelle einer Funktion zu finden ist das Newtonsche Iterationsverfahren.
30px Merke
Newtonsche Iterationsformel Diese Formel steht auch in der Merkhilfe |
a) x1 = 3,2235
Diese Lösung soll nochmals ausführlich dargestellt werden. Man erhält x1 indem man im Punkt P(x0),f(x0) auf dem Graphen von f die Tangente macht.
Es ist f(5) = 53+52+1=151.
Die Steigung der Tangente erhält man durch f'(5).
Die Ableitungsfunktion f' ist durch f(x) = 3x2+2x gegeben. Es ist f'(5) = 85.
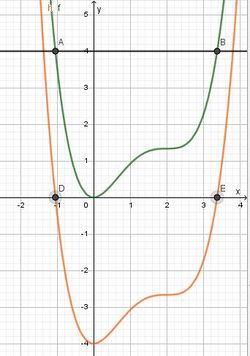
Den Schnittpunkt der Tangente mit der x-Achse ist nun x1 und x1 erhält man nun durch die Formel 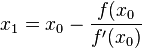 .
.
Es ist also 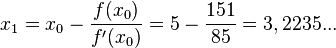
b) x1 = 3,3552
a) x26 = - 1,46557
b) x6 = 1,51598
84/10 Da 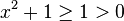 ist hat f keine Definitionslücken und auch keine Polstellen.
ist hat f keine Definitionslücken und auch keine Polstellen.
x = 1 ist doppelte Nullstelle.
Der Grenzwert für 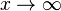 ist wegen Zählergrad = Nennergrad gleich 2 und die waagrechte Asymptote y = 2.
ist wegen Zählergrad = Nennergrad gleich 2 und die waagrechte Asymptote y = 2.
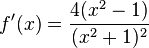
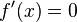 für x = -1 oder x = 1. Wegen VZW +/- ist bei (-1;4) ein HP und wegen VZW -/+ ist bei (1;0) ein TP.
für x = -1 oder x = 1. Wegen VZW +/- ist bei (-1;4) ein HP und wegen VZW -/+ ist bei (1;0) ein TP.
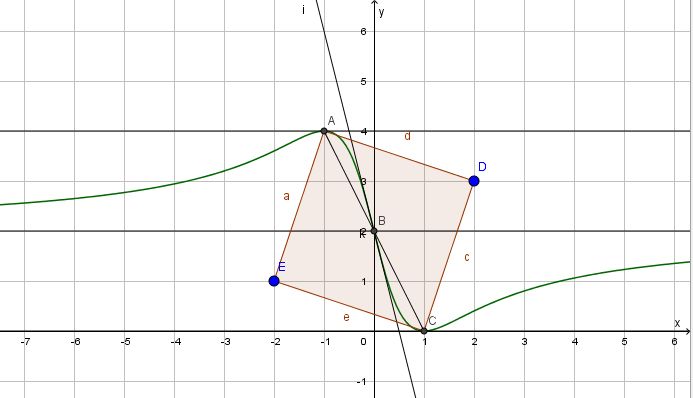
Der Flächeninhalt des Rechtecks ist AR = 8 und des Quadrats ist AQ = 10, also ist AQ umd 25% größer als AR.
84/11 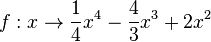
Gf hat Schnittpunkt mit der y-Achse (0;0), da f(0)=0 ist und
Schnittpunkt mit der x-Achse (0;0), da 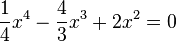
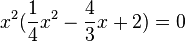
Ein Produkt ist 0, wenn ein Faktor 0 ist, also 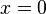 oder
oder 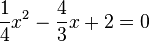 .
Die quadratische Gleichung hat keine Lösung, da ihre Diskriminante
.
Die quadratische Gleichung hat keine Lösung, da ihre Diskriminante 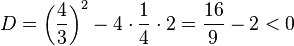
Also ist x=0 doppelte Nullstelle.
Für die Monotonietabelle braucht man 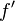 . Es ist
. Es ist 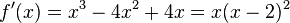
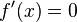 für
für 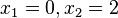 , wobei x2=2 zweifach ist.
, wobei x2=2 zweifach ist.
Gf' ist der Graph eines Polynoms 3. Grades mit Nullstelle bei x1=0 und x2=2 (doppelt), also hat man bei x2=2 keinen Vorzeichenwechsel.
Monotonietabelle:
Für x < 0 ist f'(x) < 0 und Gf ist streng monoton fallend.
Für x = 0 ist f'(0) = 0 und (0;0) ist wegen VZW -/+ ein TP.
Für 0 < x < 2 ist f'(x) > 0 und Gf ist streng monoton steigend.
Für x = 2 ist f'(2) = 0 und Gf hat dort einen Terrassenpunkt, da kein VZW.
Für x > 0 ist f'(x) > 0 und Gf ist streng monoton steigend.
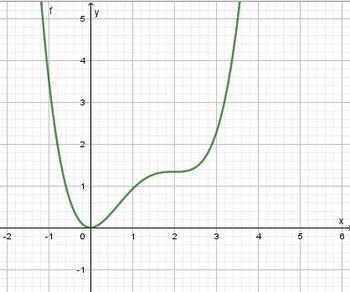
Für den letzten Teil der Aufgabe 84/11 geht es darum die x-Koordinaten der Punkte A und B zu bestimmen, eigentlich nur dei x-Koordinate von B.
Man muss also x so finden, dass die Gleichung 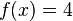 erfüllt ist. Es ist also die Gleichung
erfüllt ist. Es ist also die Gleichung
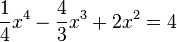
zu lösen, was gleichbedeutend ist Nullstellen der Funktion  mit
mit 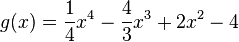 zu finden. Man muss also die Gleichung
zu finden. Man muss also die Gleichung
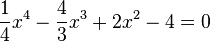
lösen. Hierfür gibt es keine Lösungsformel und das Rezept vom letzten Jahr, dass man eine Nullstelle "rät" und dann Polynomdivision macht geht hier auch nicht. Also bleibt nur das Newton-Verfahren übrig.
Es geht also darum die x-Koordinaten der Punkte D und E zu bestimmen.
Für das Newton-Verfahren hängt es stark ab welchen Startwert x0 man nimmt. Wir probieren es mit x0 = 1.
Mit 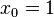 ist
ist 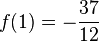 ,
, 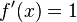 und
und 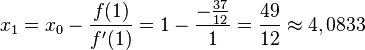
Es ist dann 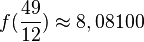 und
und 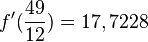 und
und 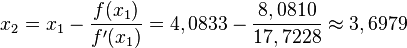
Im Graph schaut das so aus:
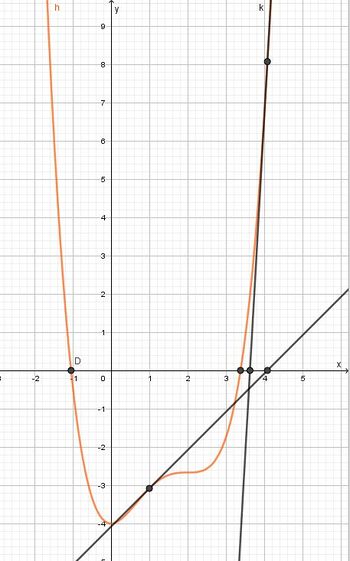 Es geht weiter mit
Es geht weiter mit 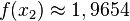 und
und 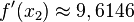 und
und 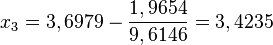 und
und
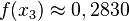 und
und 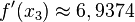 und
und 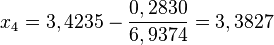 und
und
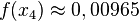 und
und 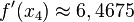 und
und 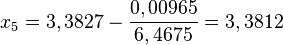
Damit ändert sich auf zwei Nachkommastellen die Nullstelle nicht mehr, es ist also 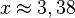
Mit einer Tabellenkalkulation geht es natürlich viel schneller und übersichtlicher.
Das schöne dabei ist, dass man den Startwert leicht ändern und in einer Tabelle die Annäherung an die Nullstelle gut nachvollziehen kann.
Wieso geht <0 = 2 nicht als Startwert?
Bei Startwerten x0 > 1 kommt man stets zu unserer Nullstelle 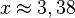 .
.