M9 Quadratische Gleichungen: Unterschied zwischen den Versionen
(→Lösungsformel) |
(→Lösungsformel) |
||
| Zeile 155: | Zeile 155: | ||
{{Merksatz|MERK=Die Lösungen der quadratischen Gleichung ax<sup>2</sup> + bx +c = 0 sind <br> | {{Merksatz|MERK=Die Lösungen der quadratischen Gleichung ax<sup>2</sup> + bx +c = 0 sind <br> | ||
<math> x_{1,2} = \frac{-b \pm \sqrt{b^2 -4ac}}{2a}</math> }} | <math> x_{1,2} = \frac{-b \pm \sqrt{b^2 -4ac}}{2a}</math> }} | ||
| + | |||
| + | Der Term b<sup>2</sup> - 4ac unter der Wurzel heißt '''Diskriminante''' und gibt an wie viele Lösungen die Gleichung hat. Es gibt nur eine Lösung, wenn b<sup>2</sup> - 4ac ≥ 0 ist. Falls b<sup>2</sup> - 4ac < 0 ist, dann hat die quadratische Gleichung keine Lösung, da in den reellen Zahlen unter einer Wurzel keine negative Zahl stehen darf. | ||
| + | |||
| + | {{Merke|1=b<sup>2</sup> - 4ac ist die '''Diskriminante''' D der quadratischen Gleichung ax<sup>2</sup> + bx + c = 0. D = b<sup>2</sup> - 4ac<br> | ||
| + | Ist D < 0, so hat die quadratische Gleichung keine Lösung. <br> | ||
| + | Ist D = 0, so hat die quadratische Gleichung eine Lösung <math>x_0 = -\frac{b}{2a}</math>.<br> | ||
| + | Ist D ≥ 0, so hat die quadratische Gleichung zwei Lösungen <math>x_1 = \frac{-b-\sqrt{b^2-4ac}}{2a}</math> und <math>x_2 = \frac{-b+\sqrt{b^2-4ac}}{2a}</math>. }} | ||
Version vom 6. Januar 2021, 08:06 Uhr
Bei den linearen Funktionen war es nützlich die Schnittpunkte des Graphen mit den Koordinatenachsen zu bestimmen. Der Schnittpunkt mit der y-Achse war der y-Abschnitt t und mit Hilfe der Nullstelle (Schnittpunkt mit der x-Achse) konnte man leicht die Steigung mbestimmen.
Bei den quadratischen Funktionen geht dies ähnlich. Der Schnittpunkt mit der y-Achse ist durch f(0) gegeben. Die Nullstelle/Nullstellen erhält man durch Lösen der Gleichung f(x) = 0.
Bei den Übungen zu den quadratischen Funktionen hast du bei Aufgabe 1 und Aufgabe 2 gesehen, dass eine Parabel zwei Nullstellen oder keine Nullstelle haben kann. Von der Normalparabel kennst du, dass sie eine Nullstelle hat.
Um die Nullstellen zu bestimmen muss man die Lösungen der Gleichung f(x) = 0 finden.
Für eine quadratische Funktion 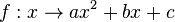 führt dies zur Gleichung
führt dies zur Gleichung 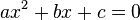 .
.
|
Merke:
Eine Gleichung der Form |
Inhaltsverzeichnis |
graphische Lösung
Manchmal kann man aus dem Graph die Nullstellen direkt ablesen. Man spricht dann vom graphischen Lösen der quadratischen Gleichung. Bei der quadratischen Funktion 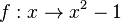 hast du folgenden Graph
hast du folgenden Graph
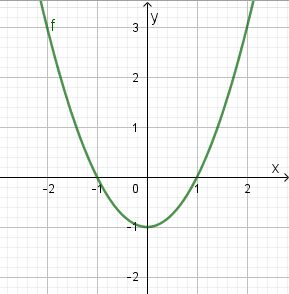
Du liest hier problemlos 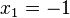 und
und 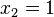 als Nullstellen der Funktion ab.
als Nullstellen der Funktion ab.
a) x1 = 0 und x2 = 2, y = (x-1)2-1
b) x1 = -2 und x2 = 0, y = -(x+1)2+1
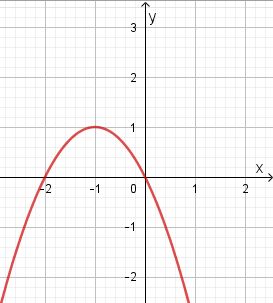
Bei dem Graphen von Aufgabe 1c kann man die Nullstellen nur näherungsweise ablesen. Man sieht jedenfalls, dass x1 = 0 und x2 = 3 nicht die Nullstellen sind, sondern, dass sie etwas daneben liegen. Aus dem Graphen kann man sie dann nur ungefähr ablesen.
1a) x = -2 , b) x1 = -2 und x2 = 3 , c) x1 = -2 und x2 = 1
Von der letzten Aufgabe weißt man, dass die Gleichung 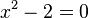 die zwei Lösungen
die zwei Lösungen 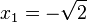 und
und 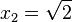 hat. Auch hier kann man graphisch nur Näherungslösungen bestimmen.
hat. Auch hier kann man graphisch nur Näherungslösungen bestimmen.
Dies ist natürlich unbefriedigend. Man möchte ja gerne die exakten Lösungen. Also muss man eine rechnerische Lösung finden.
rechnerische Lösung
Zerlegung in Linearfaktoren
Bei der Gleichung x2 + 5x = 0 kann man x ausklammern. Es ist x2 + 5x = x(x+5), also muss man die Gleichung x(x+5)=0 lösen. Man weiß
Ein Produkt hat den Wert Null, wenn ei Faktor den Wert Null hat.
Dann sind die zwei Lösungen der Gleichung x(x+5)=0 die zwei Zahlen x1=-5 und x2=0. Damit hat die Gleichung x2 + 5x = 0 auch diese zwei Lösungen x1=-5 und x2=0.
In diesem Video wird Ausklammern und die Verwendung der binomischen Formeln aufgezeigt.Ausklammern funktioniert bei der Gleichung x2 +5x + 6 = 0 nicht!
Bei den ersten beiden Summanden könnte man x ausklammern, aber der dritte Summand 6 bleibt dann stehen. x2 +5x + 6 =x(x+5)+6 und wie soll man x(x+5)+6 = 0 lösen?
Wenn man bei der ganzen rechten Seite x ausklammert, dann erhält man 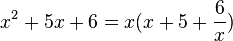 und für die Gleichung
und für die Gleichung 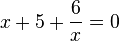 hat man keinen Plan wie man sie lösen soll.
hat man keinen Plan wie man sie lösen soll.
Schön wäre es, wenn man den Term x2 +5x + 6 so umformen könnte, dass x2 +5x + 6 = (x+3)(x+2) da steht. Dann hätte man wieder, dass ein Produkt 0 ist, wenn ein Faktor 0 ist. Also wären die Lösungen x1=-3 und x2=-2.
1. Man multipliziert die rechte Seite aus (x+3)(x+2)=x2+3x+2x+6=x2+5x+6 und erhält die linke Seite.
Doch wie kommt man auf so eine Zerlegung?
Zuerst schaut man sich den Summanden ohne x, also hier 6 an. Beim Ausmultiplizieren entsteht die 6 als Produkt der zwei Zahlen 2 und 3. Also schaut man welche natürliche Zahlen als Produkt 6 ergeben. Hier kommen 6·1 = 6 und 2·3=6 also die zwei Zahlenpaar 6 und 1 sowie 3 und 2 in Frage. Beim Ausmultiplizieren der Klammern sieht man auch, dass der Term mit x als Koeffizient die Summe der beide Zahlen hat, also 6+1 = 7 bzw. 3+2=5. Damit hat man (x+3)(x+2)=x2 + 5x + 6.
|
Um die Zerlegung von x2 + bx + c in Linearfaktoren zu finden, schaue nach natürlichen Zahlen x1 und x2, Die quadratische Gleichung x2 + bx + c = 0 hat dann die zwei Lösungen -x1 und -x2. |
Beispiele:
| x2 + 7x + 6 | 1. 6 ist das Produkt aus 6 und 1 sowie 3 und 2 2. Summe: 6+1 = 7, 3+2 = 5 3. x2 + 7x + 6 =(x+1)(x+6) |
| x2 - 8x + 12 | 1. 12 ist das Produkt aus 12 und 1, sowie 6 und 2, sowie 4 und 3. 2. Summe: 12+1 = 13, 6 + 2 = 8, 4+3=7 3. 2 und 6 sind die Kandidaten. Da vor 8 ein Minuszeichen steht muss man -2 und -6 nehmen. x2 - 8x + 12 =(x-2)(x-6) |
| x2 -5x + 6 | 1. 6 ist das Produkt aus 6 und 1 sowie 3 und 2 2. Summe: 6+1 = 7, 3+2 = 5 3. 2 und 3 sind die Kandidaten. Da vor x aber -5 steht, muss man -3 und -2 nehmen, also x2 - 5x + 6 =(x-3)(x-2) |
| x2 + x - 6 | 1. 6 ist das Produkt aus 6 und 1 sowie 2 und 3. Da nun aber hier -6 steht muss man jeweils eine Zahl mit - versehen, also (6 und -1) oder (-6 und 1) oder (-2 und 3) oder (-3 und 2). 2. Summe 6-1=5, -6+1=-5, -2+3=1, -3+2=-1, also sind -2 und 3 die passenden Zahlen. |
François Viète hat dies etwas anders herausgefunden.
Sind x1 und x2 die zwei Lösungen der Gleichung x2 + bx + c = 0, dann lässt sich der quadratische Term x2 + bx + c in Faktoren x - x1 und x - x2 zerlegen. Es ist x2 + bx + c = (x - x1)(x - x2).
Hier steht nun in der Klammer jeweils ein - Zeichen, da ja die Zahlen eingesetzt 0 ergeben!
Multipliziert man die rechte Seite aus (x - x1)(x - x2) = x2 - x·x2 - x1·x + x1·x2=x2-(x1+x2)·x+x1·x2
Der Vergleich von x2-(x1+x2)·x+x1·x2 mit x2 + bx + c liefert
b = -(x1+x2) und c = x1·x2
|
Satz von Vieta |
In dem Satz von Vieta wurden p und q verwendet. Dies ist allgemein so üblich, wenn in der quadratischen Gleichung der Koeffizient von x2 die Zahl 1 ist. Die quadratische Gleichung hat dann die Form x2 + px + q = 0.
1a) x1=-11, x2=2
b) x1=3, x2=10
c) x1=4, x2=-2
d) x1=-3, x2=-78
2a) x1=-3, x2=7
b) x1=-5, x2=2
c) x1=-2, x2=1
d) x1=2, x2=3
Lösungsformel
Das Zerlegen in Linearfaktoren oder der Satz des Vieta funktionieren oft wunderbar. Allerdings muss der Koeffizient von x2 stets 1 sein. Was macht man, wenn das nicht der Fall ist?
Was ist aber, wenn man eine Gleichung x2 - 5x + 5 = 0 hat? Da kommt man mit unserem obigen Verfahren nicht weiter. Die Zahl 5 ist das Produkt der Zahlen 5 und 1. Die Summe 5+1=6. Das ist nicht -5! Was macht man nun?
Wir betrachten den Fall 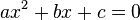 wobei
wobei 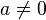 ist. Wenn a = 0 wäre, hätten wir keine quadratische Gleichung, sondern eine lineare Gleichung.
ist. Wenn a = 0 wäre, hätten wir keine quadratische Gleichung, sondern eine lineare Gleichung.
Im folgenden verzichten wir nun darauf 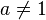 zu fordern. Das Beispiel x2 - 5x + 5 = 0 zeigt, dass wir auch das nicht lösen können.
zu fordern. Das Beispiel x2 - 5x + 5 = 0 zeigt, dass wir auch das nicht lösen können.
Eine quadratische Funktion wird normalerweise in der Form 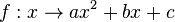 angegeben.
angegeben.
Mit Hilfe der quadratischen Ergänzung bringt man den Funktionsterm 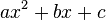 in die Scheitelform
in die Scheitelform ![a [(x + (\frac{b}{2a}))^2 - (\frac{b}{2a})^2 + \frac{c}{a}] = a [x + (\frac{b}{2a})]^2 - \frac{b^2}{4a} + c](/images/math/7/e/4/7e40844c99536921b7758405f15c81aa.png)
Die beiden Funktionsterme sind gleichwertig, es ist ![ax^2 +bx +c = a [x + (\frac{b}{2a})]^2 - \frac{b^2}{4a} + c](/images/math/a/2/5/a2503ceb9b4b49736fa3209170986286.png) .
.
Für die quadratische Gleichung 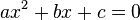 bedeutet dies, dass sie gleichwertig ist zur Gleichung
bedeutet dies, dass sie gleichwertig ist zur Gleichung ![a [x + (\frac{b}{2a})]^2 - \frac{b^2}{4a} + c = 0](/images/math/2/6/e/26ef42f4a433630473558a6f429b789b.png)
Division durch a (das ist erlaubt, da 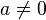 ist) ergibt die Gleichung
ist) ergibt die Gleichung ![[x + (\frac{b}{2a})]^2 - \frac{b^2}{4a^2} + \frac{c}{a} = 0](/images/math/2/3/e/23eca023d8a19c53e9a1bcdf671d45d9.png)
Nun löst man die Gleichung nach x auf. Man erhält dann ![[x + (\frac{b}{2a})]^2 = \frac{b^2}{4a^2} - \frac{c}{a}](/images/math/4/5/f/45f3d561a49af8d7b9bcfb3efd11d927.png) .
.
Auf der linken Seite steht ein Quadrat, auf der rechten Seite ein Term. Zieht man nun auf beiden Seiten die Wurzel so erhält
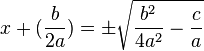
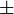 vor der Wurzel bedeutet, dass sowohl die negatitve wie die positive Wurzel quadriert den Term auf der linken Seite ergibt.
vor der Wurzel bedeutet, dass sowohl die negatitve wie die positive Wurzel quadriert den Term auf der linken Seite ergibt.
Isoliert man x auf der linken Seite so erhält man 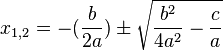
Der Indix 1,2 von x bedeutet, dass es für x zwei Werte gibt je nachdem ob vor der Wurzel ein - oder ein + steht.
Es geht jetzt nur noch darum diese Formel in eine einprägsame Form zu bringen. Dazu bringt man den Term unter der Wurzel auf den gemeinsamen Nenner 4a2 bringt, also 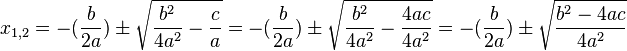
4a2 ist ein Quadrat, welches man aus der Wurzel herausziehen kann. Es ist also 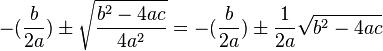
Dies ergibt weiter 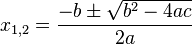
|
Merke:
Die Lösungen der quadratischen Gleichung ax2 + bx +c = 0 sind |
Der Term b2 - 4ac unter der Wurzel heißt Diskriminante und gibt an wie viele Lösungen die Gleichung hat. Es gibt nur eine Lösung, wenn b2 - 4ac ≥ 0 ist. Falls b2 - 4ac < 0 ist, dann hat die quadratische Gleichung keine Lösung, da in den reellen Zahlen unter einer Wurzel keine negative Zahl stehen darf.
|
b2 - 4ac ist die Diskriminante D der quadratischen Gleichung ax2 + bx + c = 0. D = b2 - 4ac |

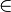 R\{0}, b, c
R\{0}, b, c 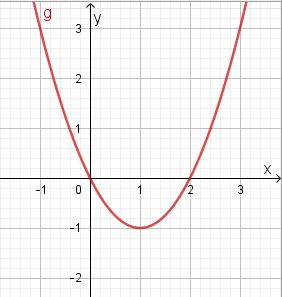
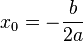 .
.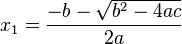 und
und 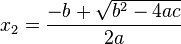 .
.

