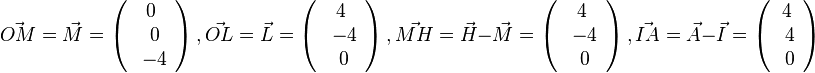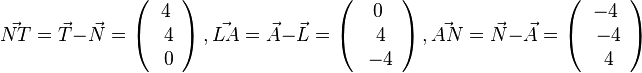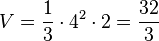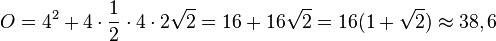M11 Aufgabe zu Vektoren: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 22: | Zeile 22: | ||
Buch S. 93 / 3b | Buch S. 93 / 3b | ||
| − | {{Lösung versteckt|1=< | + | {{Lösung versteckt|1=<math>\vec {AB} = \left ( \begin{array}{c} 2 \\\ 1 \\\ 2 \end{array}\right), \vec {DC}=\left ( \begin{array}{c} -2 \\\ -1 \\\ 0 \end{array}\right)</math> }} |
| − | + | ||
| − | < | + | <ggb_applet height="500" width="600" |
| + | filename="93-3b.ggb" /> | ||
Buch S. 93 / 4 | Buch S. 93 / 4 | ||
| Zeile 33: | Zeile 33: | ||
O(0,0,0) und M(0,0,-4) bedeuten, dass die untere Fläche 4 unterhalb der oberen Fläche liegt.<br> | O(0,0,0) und M(0,0,-4) bedeuten, dass die untere Fläche 4 unterhalb der oberen Fläche liegt.<br> | ||
Damit: T(4;0;0) liefert A(4;0;-4), N(0;-4;0) liefert I(0;-4;-4) | Damit: T(4;0;0) liefert A(4;0;-4), N(0;-4;0) liefert I(0;-4;-4) | ||
| − | Nun ergeben sich noch H(4;-4;-4), A(4;0;-4), M(0,0,-4). | + | Nun ergeben sich noch H(4;-4;-4), A(4;0;-4), M(0,0,-4).<br> |
Also insgesamt: H(4;-4;4), A(4;0;-4), M(0;0;-4), I(0;-4;-4) und L((4;-4;0), T(4;0;0), O(0;0;0), N(0;-4;0)<br> | Also insgesamt: H(4;-4;4), A(4;0;-4), M(0;0;-4), I(0;-4;-4) und L((4;-4;0), T(4;0;0), O(0;0;0), N(0;-4;0)<br> | ||
| − | |||
| − | |||
Da O der Ursprung ist, ist ein Vektor <math>\vec {OM}</math> mit Startpunkt O der Ortsvektor <math>\vec M</math>. | Da O der Ursprung ist, ist ein Vektor <math>\vec {OM}</math> mit Startpunkt O der Ortsvektor <math>\vec M</math>. | ||
| Zeile 44: | Zeile 42: | ||
b) Die Pyramide hat ein Quadrat mit Seitenlänge a = 4 als Grundfläche und die Pyramidenhöhe 2, also ist <math>V=\frac{1}{3} \cdot 4^2 \cdot 2=\frac{32}{3}</math><br> | b) Die Pyramide hat ein Quadrat mit Seitenlänge a = 4 als Grundfläche und die Pyramidenhöhe 2, also ist <math>V=\frac{1}{3} \cdot 4^2 \cdot 2=\frac{32}{3}</math><br> | ||
Die Oberfläche hat den Inhalt <math>O=4^2 + 4\cdot \frac{1}{2}\cdot 4 \cdot 2\sqrt 2 = 16+16\sqrt 2=16(1+\sqrt 2) \approx 38,6</math> }} | Die Oberfläche hat den Inhalt <math>O=4^2 + 4\cdot \frac{1}{2}\cdot 4 \cdot 2\sqrt 2 = 16+16\sqrt 2=16(1+\sqrt 2) \approx 38,6</math> }} | ||
| + | |||
| + | <ggb_applet height="500" width="600" | ||
| + | filename="93-4.ggb" /> | ||
Version vom 9. Januar 2021, 18:24 Uhr
Buch S. 93 / 1 d, e
Buch S. 93 / 2
Buch S. 93 / 3b
Buch S. 93 / 4
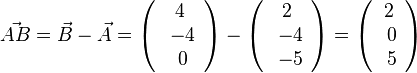
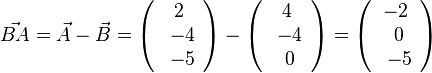
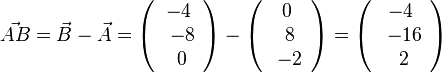
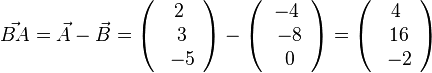
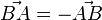
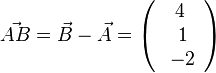 , also
, also 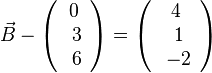 oder
oder 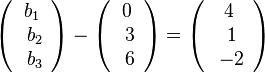 liefert
liefert 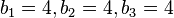 .
.
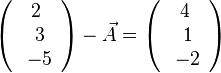 oder
oder 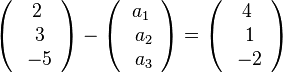 liefert
liefert 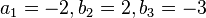 .
.
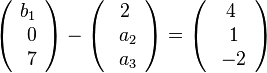 liefert
liefert 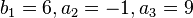
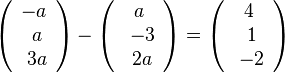 liefert
liefert 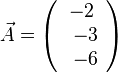 und
und 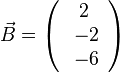
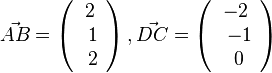
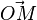 mit Startpunkt O der Ortsvektor
mit Startpunkt O der Ortsvektor 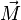 .
.