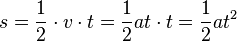Ph9 tx- und tv- Abhängigkeiten: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
* Bewegung mit konstanter Geschwindigkeit und | * Bewegung mit konstanter Geschwindigkeit und | ||
* Bewegung mit konstanter Beschleunigung | * Bewegung mit konstanter Beschleunigung | ||
| + | |||
Für beide Bewegungen sammeln wir zuerst unsere bisherigen Kenntnisse: | Für beide Bewegungen sammeln wir zuerst unsere bisherigen Kenntnisse: | ||
| Zeile 30: | Zeile 31: | ||
{{Aufgaben-blau|2|2=Schaue dir dies Video an und notiere die Fakten<br> | {{Aufgaben-blau|2|2=Schaue dir dies Video an und notiere die Fakten<br> | ||
| − | {{#ev:youtube |EmDGwpoJQiE|350}} | + | <center>{{#ev:youtube |EmDGwpoJQiE|350}} </center> }} |
{{Merke|1=Bei einer gleichmäßig beschleunigten Bewegung bewegt sich ein Körper geradlinig und wird mit konstanter Beschleunigung beschleunigt. <br> | {{Merke|1=Bei einer gleichmäßig beschleunigten Bewegung bewegt sich ein Körper geradlinig und wird mit konstanter Beschleunigung beschleunigt. <br> | ||
a = konstant<br> | a = konstant<br> | ||
Im ta-Diagramm wird nach rechts die Zeit t und nach oben die Beschleunigung a aufgetragen. <br> | Im ta-Diagramm wird nach rechts die Zeit t und nach oben die Beschleunigung a aufgetragen. <br> | ||
| − | + | <center>[[Datei:Ta-diagramm 2.jpg|350px]]</center><br> | |
Im tv-Diagramm wird nach rechts die Zeit t und nach oben die Geschwindigkeit v aufgetragen. <br> | Im tv-Diagramm wird nach rechts die Zeit t und nach oben die Geschwindigkeit v aufgetragen. <br> | ||
| + | <center>[[Datei:Tv-diagramm 2.jpg|350px]]</center><br> | ||
| + | Beschleunigung <math>a=\frac{\Delta v}{\Delta t} </math>, da a konstant ist gilt auch <math>a = \frac{v}{t}</math>.<br> | ||
| + | Die Fläche unter dem Graph im ta-Diagramm stellt die Geschwindigkeit v dar. Es ist <math>v = a \cdot t</math>.<br> | ||
| + | Im ts-Diagramm wird nach rechts die Zeit t und nach oben der zurückgelegte Weg s aufgetragen.<br> | ||
| + | <center>[[Datei:Ts-Diagramm 2.jpg|350px]]</center><br> | ||
| + | Auch hier stellt die Fläche unter dem Graph im tv-Diagramm den zurückgelegtn Weg s dar. Es ist <math>s=\frac{1}{2}\cdot v\cdot t = \frac{1}{2} at\cdot t=\frac{1}{2} at^2</math> | ||
| − | + | Formeln: | |
| − | + | <center>a = konstant<br> | |
| − | }} | + | <math> v = a \cdot t</math> oder <math>a = \frac{v}{t}</math><br> |
| + | <math>s = \frac{1}{2}at^2</math></center> }} | ||
Version vom 18. Januar 2021, 08:29 Uhr
Ihr habt schon zwei Arten von Bewegungen kennengelernt:
- Bewegung mit konstanter Geschwindigkeit und
- Bewegung mit konstanter Beschleunigung
Für beide Bewegungen sammeln wir zuerst unsere bisherigen Kenntnisse:
1. Gleichförmige Bewegung:
30px Merke
Bei einer gleichförmigen Bewegung bewegt sich ein Körper geradlinig mit konstanter Geschwindigkeit v = konstant. 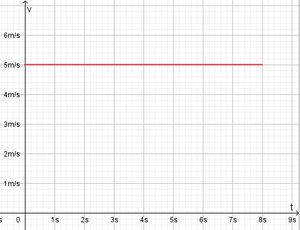 Im ts-Diagramm wird auch nach rechts die Zeit t aber nach oben der zurückgelegte Weg s aufgetragen. 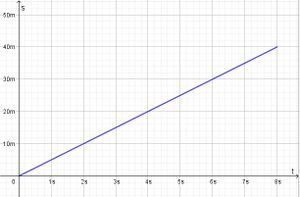 Die Strecke beginnt im Ursprung und steigt linear an. Formeln:
 |
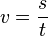Die Fläche unter der Kurve im tv-Diagramm ist eine Rechtecksfläche und berechnet sich als v·t.
Sie stellt den zurückgelegten Weg s dar.
2. Gleichmäßig beschleunigte Bewegung:
30px Merke
Bei einer gleichmäßig beschleunigten Bewegung bewegt sich ein Körper geradlinig und wird mit konstanter Beschleunigung beschleunigt. 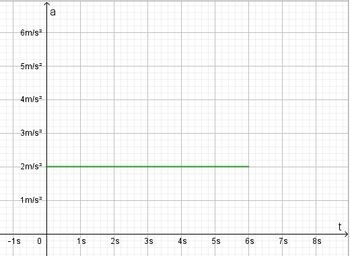 Im tv-Diagramm wird nach rechts die Zeit t und nach oben die Geschwindigkeit v aufgetragen. 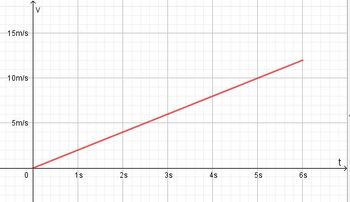 Beschleunigung 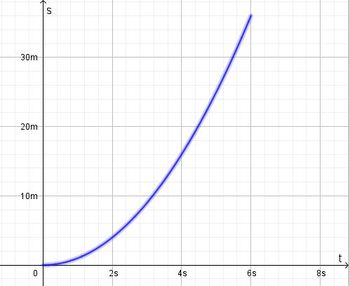 Auch hier stellt die Fläche unter dem Graph im tv-Diagramm den zurückgelegtn Weg s dar. Es ist Formeln:
 |
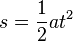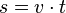
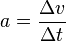, da a konstant ist gilt auch 
.
.
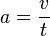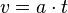