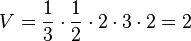Diskussion:M11 Skalarprodukt: Unterschied zwischen den Versionen
| Zeile 26: | Zeile 26: | ||
[[Datei:113-19.jpg]]<br> | [[Datei:113-19.jpg]]<br> | ||
Der Winkel ALF bezeichne ich mit <math>\alpha</math>. Es ist <math>cos \alpha = \frac{\vec {LA}\circ \vec {LF}}{|\vec{LA}||\vec {LF}}=\frac{\left ( \begin{array}{c} 0 \\\ -3 \\\ 4 \end{array}\right) \circ \left ( \begin{array}{c} 4 \\\ -3 \\\ 0 \end{array}\right)}{5\cdot 5}=\frac{9}{25}</math> und <math>\alpha = 68,9^o</math><br> | Der Winkel ALF bezeichne ich mit <math>\alpha</math>. Es ist <math>cos \alpha = \frac{\vec {LA}\circ \vec {LF}}{|\vec{LA}||\vec {LF}}=\frac{\left ( \begin{array}{c} 0 \\\ -3 \\\ 4 \end{array}\right) \circ \left ( \begin{array}{c} 4 \\\ -3 \\\ 0 \end{array}\right)}{5\cdot 5}=\frac{9}{25}</math> und <math>\alpha = 68,9^o</math><br> | ||
| − | Das Volumen der Pyramide ist <math>V=\frac{1}{3}\cdot 3 \cdot 4 \cdot 4= | + | Das Volumen der Pyramide ist <math>V=\frac{1}{3}\cdot \frac{1}{2} \cdot 3 \cdot 4 \cdot 4=8</math> |
| − | 113/20 | + | 113/20<br> |
| + | Es ist <math>\vec {AB}=\left ( \begin{array}{c} 2 \\\ -3 \\\ 0 \end{array}\right), \vec {BC_a}=\left ( \begin{array}{c} 0 \\\ 3 \\\ a-2 \end{array}\right), \vec {AC_a}=\left ( \begin{array}{c} 2 \\\ 0 \\\ a-2 \end{array}\right)</math><br> | ||
| + | Es ist <math>\vec {AB} \circ \vec {AC_a}= \left ( \begin{array}{c} 2 \\\ -3 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 2 \\\ 0 \\\ a-2 \end{array}\right) = 4+0+0=4</math>, also ist bei A kein rechter Winkel.<br> | ||
| + | Es ist <math>\vec {BA} \circ \vec {BC_a}=\left ( \begin{array}{c} -2 \\\ 3 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 3 \\\ a-2 \end{array}\right) = 0+9+0=9</math>, also ist bei B kein rechter Winkel.<br> | ||
| + | Das Dreieck ABC<sub>a</sub> hat bei C<sub>a</sub> den rechten Winkel. Nun sucht man den Wert von a, für den das Skalarprodukt <math>\vec {C_aA} \circ \vec {C_aB}=0</math> ist.<br> | ||
| + | <math>\vec {C_aA} \circ \vec {C_aB}=\left ( \begin{array}{c} -2 \\\ 0 \\\ 2-a \end{array}\right ) \circ \left ( \begin{array}{c} 0 \\\ -3 \\\ 2-a \end{array}\right)=0+0+(2-a)^2=0</math> für <math>a=2</math>.<br> | ||
| + | Die Grundfläche der Pyramide liegt in einer zur x<sub>1</sub>x<sub>2</sub>-Ebene parallelen Ebene im Abstand 2. Das Volumen der Pyramide ist dann <math>V= \frac{1}{3}\cdot \frac{1}{2}\cdot 2 \cdot 3 \cdot 2 = 2</math><br> | ||
| + | __NOCACHE__ | ||
| + | <ggb_applet height="600" width="600" | ||
| + | filename="113-20.ggb" /> | ||
Version vom 25. Januar 2021, 08:19 Uhr
Buch S. 112 / 10
Die Vektoren  und
und  stehen senkrecht aufeinander, d.h.
stehen senkrecht aufeinander, d.h. 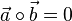 .
.
a) 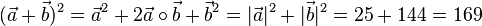
b) 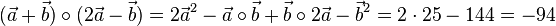
c) Eine Hommage an die binomischen Formeln!
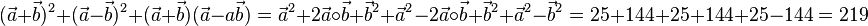
Buch S. 112 / 14
Man weiß aus der Mittelstufe, dass der Flächeninhalt eines Parallelogramms A = gh ist. D.h. fälllt man von der Spitze von 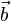 das Lot auf
das Lot auf  erhält man die Höhe h.
erhält man die Höhe h.
a steht für 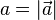 und b für
und b für 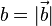 . Es ist dann
. Es ist dann 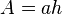 und h ist
und h ist 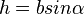 , also
, also 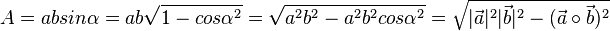 q.e.d.
q.e.d.
b) 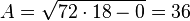 (Beachten Sie, dass
(Beachten Sie, dass  und
und 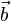 senkrecht zueinander sind.
senkrecht zueinander sind.
c) 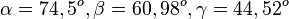 ,
, 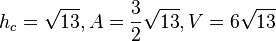
112/15 In dieser Aufgabe wird ein bekannter Satz der Mittelstufe mit Vektoren bewiesen. Man soll zeigen, dass der Winkel ACB gleich 90o ist. Dies macht man mit dem Skalarprodukt. Wenn das Skalarprodukt der Vektoren 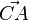 und
und 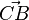 gleich 0 ist, dann ist bei C ein rechter Winkel.
gleich 0 ist, dann ist bei C ein rechter Winkel.
Man drückt 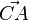 und
und 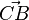 durch
durch 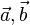 aus. Es ist
aus. Es ist 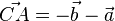 und
und 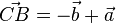 .
.
Man sieht aus der Zeichnung, dass 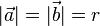 ist.
ist.
Das Skalarprodukt ist dann 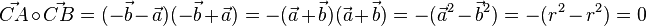
Buch S. 113 / 16
A(2;0,0), B(0;2;0), C(0;0;2) und S(0;0;0)
a) siehe Definition des Skalarprodukts
b) 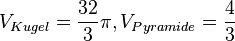 . Es ist
. Es ist 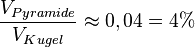
113/19
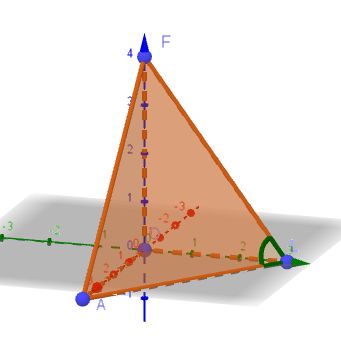
Der Winkel ALF bezeichne ich mit 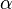 . Es ist
. Es ist 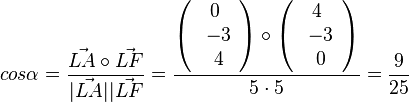 und
und 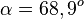
Das Volumen der Pyramide ist 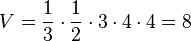
113/20
Es ist 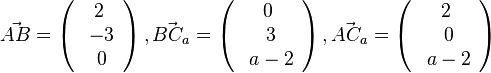
Es ist 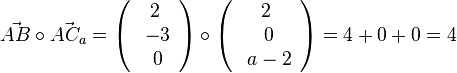 , also ist bei A kein rechter Winkel.
, also ist bei A kein rechter Winkel.
Es ist 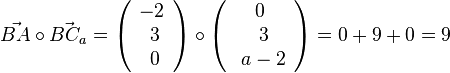 , also ist bei B kein rechter Winkel.
, also ist bei B kein rechter Winkel.
Das Dreieck ABCa hat bei Ca den rechten Winkel. Nun sucht man den Wert von a, für den das Skalarprodukt 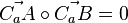 ist.
ist.
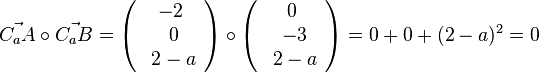 für
für  .
.
Die Grundfläche der Pyramide liegt in einer zur x1x2-Ebene parallelen Ebene im Abstand 2. Das Volumen der Pyramide ist dann