M11 Skalarprodukt: Unterschied zwischen den Versionen
| (18 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
In Physik hat man gelernt, dass Arbeit W das Produkt aus der Kraft F, die in Wegrichtung entlang des Weges s wirkt. Man schreibt dann W = F·s. Was macht man aber, wenn man einen Leiterwagen zieht? <br> | In Physik hat man gelernt, dass Arbeit W das Produkt aus der Kraft F, die in Wegrichtung entlang des Weges s wirkt. Man schreibt dann W = F·s. Was macht man aber, wenn man einen Leiterwagen zieht? <br> | ||
[[Datei:Bollerwagen.JPG|350px]]<br> | [[Datei:Bollerwagen.JPG|350px]]<br> | ||
| − | Nach unserer Arbeitsdefinition muss man den Wagen so wie er abgebildet ist nach vorne ziehen. Dazu muss man sich bücken und es ist sehr unbequem. Man wird den Handgriff hochnehmen, aber dann wirkt die Kraft nicht mehr in Wegrichtung sondern ist schräg dazu. Wie macht sich das dann in der Arbeit | + | Nach unserer Arbeitsdefinition muss man den Wagen so wie er abgebildet ist nach vorne ziehen. Dazu muss man sich bücken und es ist sehr unbequem. Man wird den Handgriff hochnehmen, aber dann wirkt die Kraft nicht mehr in Wegrichtung sondern ist schräg dazu. Wenn die Zugstange senkrecht nach oben gerichtet ist, kann man den Leiterwagen gar nicht ziehen. Wie macht sich das dann in der Arbeit bemerkbar?<br> |
Man löst das, indem man die Kraftkomponente F<sub>s</sub> in Wegrichtung betrachtet und damit die Arbeit Arbeit W = F<sub>s</sub>·s berechnet.<br> | Man löst das, indem man die Kraftkomponente F<sub>s</sub> in Wegrichtung betrachtet und damit die Arbeit Arbeit W = F<sub>s</sub>·s berechnet.<br> | ||
[[Datei:Wagen F.jpg|300px]]<br> | [[Datei:Wagen F.jpg|300px]]<br> | ||
F<sub>s</sub> ist die waagrechte Kraftkomponente von F in Fahrtrichtung. | F<sub>s</sub> ist die waagrechte Kraftkomponente von F in Fahrtrichtung. | ||
| − | In der Mathematik führt man hierzu das Skalarprodukt ein, dies wird dann in der Physik auch verwendet und man sagt dann, dass die Arbeit W das Skalarprodukt des Kraftvektors <math>\vec F</math> mit dem Wegvektor <math>\vec s</math> ist, also <math> W = \vec F \ | + | In der Mathematik führt man hierzu das Skalarprodukt ein, dies wird dann in der Physik auch verwendet und man sagt dann, dass die Arbeit W das Skalarprodukt des Kraftvektors <math>\vec F</math> mit dem Wegvektor <math>\vec s</math> ist, also <math> W = \vec F \circ \vec s</math> oder ohne Vektoren <math> W = F\cdot s \cdot cos(\varphi)</math>. |
| − | {{Merksatz|MERK= Für die Vektoren <math>\vec a=\left ( \begin{array}{c} a_1 \\\ a_2 \\\ a_3 \end{array}\right)</math> | + | {{Merksatz|MERK= Für die Vektoren <math>\vec a=\left ( \begin{array}{c} a_1 \\\ a_2 \\\ a_3 \end{array}\right)</math> und <math>\vec b=\left ( \begin{array}{c} b_1 \\\ b_2 \\\ b_3 \end{array}\right)</math> definiert man das '''Skalarprodukt''' <math>\vec a \circ \vec b = a_1 b_1 + a_2 b_2 + a_3 b_3</math>. |
| − | Das Ergebnis des Skalarprodukts <math>\vec a \ | + | Das Ergebnis des Skalarprodukts <math>\vec a \circ \vec b </math> ist eine Zahl (ein Skalar). Es ist <math>\vec a \circ \vec b = \left ( \begin{array}{c} a_1 \\\ a_2 \\\ a_3 \end{array}\right) \circ \left ( \begin{array}{c} b_1 \\\ b_2 \\\ b_3 \end{array}\right) = a_1 b_1 + a_2 b_2 + a_3 b_3</math>. |
| − | Es ist weiterhin, wenn <math>\varphi</math> der Winkel zwischen den Vektoren <math>\vec a</math> und <math>\vec b </math> ist<br> [[Datei:Skalarprodukt 1.jpg]] <math>\vec a \ | + | Für das Malzeichen verwenden wir einen Kringel <math>\circ</math>, damit man das Multiplizieren von Vektoren vom Multiplizieren von Zahlen unterscheidet. |
| + | |||
| + | Es ist weiterhin, wenn <math>\varphi</math> der Winkel zwischen den Vektoren <math>\vec a</math> und <math>\vec b </math> ist<br> [[Datei:Skalarprodukt 1.jpg]] <math>\vec a \circ \vec b =|\vec a||\vec b|cos(\varphi)</math> | ||
| + | |||
| + | <center>{{#ev:youtube |WrRVLMQPHeU|350}}</center>}} | ||
| − | |||
'''Beispiele:''' <br> | '''Beispiele:''' <br> | ||
| − | 1. <math>\vec a \ | + | 1. <math>\vec a \circ \vec b = \left ( \begin{array}{c} 2 \\\ 3 \\\ -1 \end{array}\right) \circ \left ( \begin{array}{c} 3 \\\ 2 \\\ 2 \end{array}\right) = 2\cdot 3 + 3\cdot 2 + (-1)\cdot 2=10</math>. <br> |
| − | 2. <math>\vec a \ | + | 2. <math>\vec a \circ \vec b = \left ( \begin{array}{c} -1 \\\ 2 \\\ 3 \end{array}\right) \circ \left ( \begin{array}{c} 3 \\\ 2 \\\ -2 \end{array}\right) = -1\cdot 3 + 2\cdot 2 + 3\cdot (-2)=-5</math>. <br> |
{{Merksatz|MERK=Dies führt zur Definition des Winkels. Der Winkel <math>\varphi</math> der Winkel zwischen den Vektoren <math>\vec a</math> und <math>\vec b </math> ist gegeben durch<br> | {{Merksatz|MERK=Dies führt zur Definition des Winkels. Der Winkel <math>\varphi</math> der Winkel zwischen den Vektoren <math>\vec a</math> und <math>\vec b </math> ist gegeben durch<br> | ||
| − | <center><math>cos \varphi =\frac{\vec a \ | + | <center><math>cos \varphi =\frac{\vec a \circ \vec b}{|\vec a||\vec b|} = \frac{a_1 b_1 + a_2 b_2 + a_3 b_3}{|\vec a||\vec b|}</math> }} |
'''Beispiele:'''<br> | '''Beispiele:'''<br> | ||
| − | 1. <math>\vec a =\left ( \begin{array}{c} -2 \\\ 0 \\\ 3 \end{array}\right) </math>, <math>\vec b=\left ( \begin{array}{c} 2 \\\ 2 \\\ 3 \end{array}\right)</math>. Es ist <math>|\vec a|=\sqrt {13}, |\vec b|=\sqrt {17}, \vec a \ | + | 1. <math>\vec a =\left ( \begin{array}{c} -2 \\\ 0 \\\ 3 \end{array}\right) </math>, <math>\vec b=\left ( \begin{array}{c} 2 \\\ 2 \\\ 3 \end{array}\right)</math>. Es ist <math>|\vec a|=\sqrt {13}, |\vec b|=\sqrt {17}, \vec a \circ \vec b = \left ( \begin{array}{c} -2 \\\ 0 \\\ 3 \end{array}\right) \circ \left ( \begin{array}{c} 2 \\\ 2 \\\ 3 \end{array}\right) = -2\cdot 2 + 0\cdot 2 + 3\cdot 3=5</math>. <br> |
| − | Damit ist <math>cos \varphi = \frac{\vec a \ | + | Damit ist <math>cos \varphi = \frac{\vec a \circ \vec b}{|\vec a| \cdot |\vec b|}=\frac{5}{\sqrt{13}\cdot \sqrt{17}}\approx 0,3363</math>, also <math>\varphi = 70,3^o</math><br> |
| − | 2. <math>\vec a =\left ( \begin{array}{c} -2 \\\ -1 \\\ 2 \end{array}\right) </math>, <math>\vec b=\left ( \begin{array}{c} 0 \\\ 2 \\\ 1 \end{array}\right)</math>. Es ist <math>|\vec a|=3, |\vec b|=\sqrt 5, \vec a \ | + | 2. <math>\vec a =\left ( \begin{array}{c} -2 \\\ -1 \\\ 2 \end{array}\right) </math>, <math>\vec b=\left ( \begin{array}{c} 0 \\\ 2 \\\ 1 \end{array}\right)</math>. Es ist <math>|\vec a|=3, |\vec b|=\sqrt 5, \vec a \circ \vec b = \left ( \begin{array}{c} -2 \\\ -1 \\\ 2 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 2 \\\ 1 \end{array}\right) = -2\cdot 0 + -1\cdot 2 + 2\cdot 1=0</math>. <br> |
| − | Damit ist <math>cos \varphi = \frac{\vec a \ | + | Damit ist <math>cos \varphi = \frac{\vec a \circ \vec b}{|\vec a| \cdot |\vec b|}=\frac{0}{3\cdot \sqrt 5}=0</math>, also <math>\varphi = 90^o</math>. |
| − | |||
| − | + | {{Merke|1=Haben die zwei Vektoren <math>\vec a</math> und <math>\vec b </math> gleiche Richtung, dann ist <math>\varphi = 0^o</math> und <math> cos \varphi = 1</math>. Dann ist <math>\vec a \circ \vec b = |\vec a||\vec b|</math>. | |
| − | + | ||
| + | Ist insbesondere <math>\vec b = \vec a</math>, dann ist <math>\vec a \circ \vec a = |\vec a||\vec a|=|\vec a|^2</math>. <br> | ||
| + | Hier ist das Skalarprodukt <math>\vec a \circ \vec a </math> gleich dem Quadrat des Betrags des Vektors <math>\vec a</math> . | ||
| − | |||
| + | Haben die zwei Vektoren <math>\vec a</math> und <math>\vec b </math> entgegengesetzte Richtung, dann ist <math>\varphi = 180^o</math> und <math> cos \varphi = -1</math>. Dann ist <math>\vec a \circ \vec b = -|\vec a||\vec b|</math>. | ||
| − | |||
| − | Dies giilt auch umgekehrt. Ist das Skalarprodukt <math>\vec a \ | + | Schließen die beiden Vektoren <math>\vec a</math> und <math>\vec b </math> einen Winkel <math>\varphi = 90^o</math>, dann stehen die beiden Vektoren senkrecht zueinander. Es ist <math>cos \varphi = 0</math>. Damit ist <math>\vec a \circ \vec b = |\vec a||\vec b|cos(90^o)=|\vec a||\vec b|\cdot 0=0</math>. Die beiden Vektoren <math>\vec a</math> und <math>\vec b </math> sind '''senkrecht zueinander''' oder '''orthogonal'''. |
| + | |||
| + | Dies giilt auch umgekehrt. Ist das Skalarprodukt <math>\vec a \circ \vec b = 0</math>, dann stehen die Vektoren <math>\vec a</math> und <math>\vec b </math> senkrecht zueinander . <math>\vec a</math> und <math>\vec b </math> sind '''orthogonal'''. }} | ||
{{Aufgaben-blau|1|2=1. Finden Sie einen Wert für k, so dass die Vektoren <math>\vec a = \left ( \begin{array}{c} 1 \\\ 0 \\\ 2 \end{array}\right)</math> und <math>\vec b = \left ( \begin{array}{c} k \\\ 5 \\\ 5 \end{array}\right)</math> senkrecht zueiander sind. | {{Aufgaben-blau|1|2=1. Finden Sie einen Wert für k, so dass die Vektoren <math>\vec a = \left ( \begin{array}{c} 1 \\\ 0 \\\ 2 \end{array}\right)</math> und <math>\vec b = \left ( \begin{array}{c} k \\\ 5 \\\ 5 \end{array}\right)</math> senkrecht zueiander sind. | ||
| − | 2. Weise nach, dass die Einheitsvektoren unseres dreidimensionalen Koordinatensystems senkrecht zueinander stehen. | + | 2. Weise nach, dass die Einheitsvektoren <math>\vec e_1 =\left ( \begin{array}{c} 1 \\\ 0 \\\ 0 \end{array}\right), \vec e_2=\left ( \begin{array}{c} 0 \\\ 1 \\\ 0 \end{array}\right), \vec e_3 = \left ( \begin{array}{c} 0 \\\ 0 \\\ 1 \end{array}\right)</math> unseres dreidimensionalen Koordinatensystems senkrecht zueinander stehen. |
3. Finden Sie einen Vektor <math>\vec n =\left ( \begin{array}{c} n_1 \\\ n_2 \\\ n_3 \end{array}\right)</math>, der senkrecht auf den zwei Vektoren <math>\vec a =\left ( \begin{array}{c} 1 \\\ 0 \\\ 2 \end{array}\right)</math> und <math>\vec b =\left ( \begin{array}{c} 3 \\\ 4 \\\ -2 \end{array}\right)</math> steht. }} | 3. Finden Sie einen Vektor <math>\vec n =\left ( \begin{array}{c} n_1 \\\ n_2 \\\ n_3 \end{array}\right)</math>, der senkrecht auf den zwei Vektoren <math>\vec a =\left ( \begin{array}{c} 1 \\\ 0 \\\ 2 \end{array}\right)</math> und <math>\vec b =\left ( \begin{array}{c} 3 \\\ 4 \\\ -2 \end{array}\right)</math> steht. }} | ||
| − | {{Lösung versteckt|1=<math>\vec a \ | + | {{Lösung versteckt|1=<math>\vec a \circ \vec b= \left ( \begin{array}{c} 1 \\\ 0 \\\ 2 \end{array}\right) \circ \left ( \begin{array}{c} k \\\ 5 \\\ 5 \end{array}\right)=k+0+10 = k+10</math>. Es ist k+10 = 0 für k = -10. |
| − | 2. | + | 2. Es ist <math>\vec e_1 \circ \vec e_2 = \left ( \begin{array}{c} 1 \\\ 0 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 1 \\\ 0 \end{array}\right) = 0+0+0=0</math>, <br> |
| − | Es ist <math>\vec e_1 \ | + | <math>\vec e_1 \circ \vec e_3 = \left ( \begin{array}{c} 1 \\\ 0 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 0 \\\ 1 \end{array}\right) = 0+0+0=0</math>,<br> |
| − | <math>\vec e_1 \ | + | <math>\vec e_2 \circ \vec e_3 = \left ( \begin{array}{c} 0 \\\ 1 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 0 \\\ 1 \end{array}\right) = 0+0+0=0</math><br> |
| − | <math>\vec e_2 \ | + | |
Also sind <math>\vec e_1, \vec e_2, \vec e_3</math> paarweise senkrecht zueinander. | Also sind <math>\vec e_1, \vec e_2, \vec e_3</math> paarweise senkrecht zueinander. | ||
| − | 3. Es muss sein: <math>\left ( \begin{array}{c} n_1 \\\ n_2 \\\ n_3 \end{array}\right)\ | + | 3. Es muss sein: <math>\left ( \begin{array}{c} n_1 \\\ n_2 \\\ n_3 \end{array}\right)\circ \left ( \begin{array}{c} 1 \\\ 0 \\\ 2 \end{array}\right) = n_1 + 2n_3 = 0</math> und <math>\left ( \begin{array}{c} n_1 \\\ n_2 \\\ n_3 \end{array}\right) \circ \left ( \begin{array}{c} 3 \\\ 4 \\\ -2 \end{array}\right )= 3n_1 + 4 n_2 - 2n_3 = 0</math><br> |
Man hat also zwei Gleichungen <math>n_1 + 2n_3 = 0</math> und <math>3n_1 + 4 n_2 - 2n_3 = 0</math>.<br> | Man hat also zwei Gleichungen <math>n_1 + 2n_3 = 0</math> und <math>3n_1 + 4 n_2 - 2n_3 = 0</math>.<br> | ||
Löst man die erste Gleichung nach <math>n_1</math> auf, so ist <math>n_1 = -2n_3</math>. Dies setzt man in die zweite Gleichung ein und erhält <math>3(-2n_3) + 4 n_2 - 2n_3 = 0</math>. <br> | Löst man die erste Gleichung nach <math>n_1</math> auf, so ist <math>n_1 = -2n_3</math>. Dies setzt man in die zweite Gleichung ein und erhält <math>3(-2n_3) + 4 n_2 - 2n_3 = 0</math>. <br> | ||
| Zeile 63: | Zeile 66: | ||
Wählt man <math>n_3 =1</math>, dann ist <math>n_2 = 2, n_1=-2</math> und man hat den Vektor <math>\vec n=\left ( \begin{array}{c} -2 \\\ 2 \\\ 1 \end{array}\right)</math>. <br> | Wählt man <math>n_3 =1</math>, dann ist <math>n_2 = 2, n_1=-2</math> und man hat den Vektor <math>\vec n=\left ( \begin{array}{c} -2 \\\ 2 \\\ 1 \end{array}\right)</math>. <br> | ||
<math>\vec n</math> steht senkrecht zu den Vektoren <math>\vec a, \vec b</math>.<br> | <math>\vec n</math> steht senkrecht zu den Vektoren <math>\vec a, \vec b</math>.<br> | ||
| − | Probe: <math>\left ( \begin{array}{c} -2 \\\ 2 \\\ 1 \end{array}\right) \ | + | Probe: <math>\left ( \begin{array}{c} -2 \\\ 2 \\\ 1 \end{array}\right) \circ \left ( \begin{array}{c} 1 \\\ 0 \\\ 2 \end{array}\right) = -2+2=0</math> und <math>\left ( \begin{array}{c} -2 \\\ 2 \\\ 1 \end{array}\right) \circ \left ( \begin{array}{c} 3 \\\ 4 \\\ -2 \end{array}\right )=-6+8-2=0</math> }} |
{{Merke|1=Rechengesetze für das Skalarprodukt | {{Merke|1=Rechengesetze für das Skalarprodukt | ||
Für Vektoren <math>\vec a. \vec b, \vec c</math> und reelle Zahlen r,s gilt:<br> | Für Vektoren <math>\vec a. \vec b, \vec c</math> und reelle Zahlen r,s gilt:<br> | ||
| − | * Kommutativgesetz <math>\vec a \ | + | * Kommutativgesetz <math>\vec a \circ \vec b = \vec b \circ \vec a</math><br> |
| − | * <math>(r \cdot \vec a)\ | + | * <math>(r \cdot \vec a)\circ (s \cdot \vec b)=(r\cdot s)\cdot (\vec a \circ \vec b)</math><br> |
| − | * Distributivgesetz <math>\vec a \cdot (\vec b + \vec c)=\vec a \cdot \vec b + \vec a \cdot \vec c</math> | + | * Distributivgesetz <math>\vec a \circ (\vec b + \vec c)=\vec a \circ \vec b + \vec a \circ \vec c</math> |
| + | |||
| + | Beachten Sie bitte die unterschiedlichen Malzeichen <math>\circ</math> für Vektoren und <math>\cdot</math> für Zahlen bzw. S-Multiplikation. <br> | ||
| + | Man kann hier auch wie gewohnt rechnen! }} | ||
| + | |||
| + | {{Aufgaben-blau|2|2=Buch S. 111 / 1<br> | ||
| + | Buch S. 111 / 2<br> | ||
| + | Buch S. 111 / 3 <br> | ||
| + | Buch S. 111 / 4}} | ||
| + | |||
| + | {{Lösung versteckt|1=111/1<br> | ||
| + | a) <math>cos \varphi = \frac{2+2}{\sqrt 5 \cdot \sqrt 5}=\frac{4}{5}= 0,8 </math> liefert <math>\varphi = 36,9^o</math><br> | ||
| + | b) <math>cos \varphi = \frac{0+24-+24}{\sqrt {34} \cdot 10}=\frac{0}{10\sqrt{34}}= 0</math> liefert <math>\varphi = 90^o</math><br> | ||
| + | c) <math>cos \varphi = \frac{-10-10-10}{\sqrt {12} \cdot \sqrt {75}}=\frac{-30}{30}= -1 </math> liefert <math>\varphi = 180^o</math><br> | ||
| + | d) <math>cos \varphi = \frac{0+80-6}{\sqrt {126} \cdot 10}=\frac{74}{10\sqrt{126}}= 0,6592 </math> liefert <math>\varphi = 48,8^o</math><br> | ||
| + | e) 90<sup>o</sup><br> | ||
| + | f) 31<sup>o</sup><br> | ||
| + | g) 0<sup>o</sup><br> | ||
| + | h) 180<sup>o</sup><br> | ||
| + | i) 144,7<sup>o</sup> | ||
| + | |||
| + | 111/2 a) <math>\vec a \circ \vec b = \left ( \begin{array}{c} q \\\ 3 \\\ 2 \end{array}\right) \circ \left ( \begin{array}{c} 1 \\\ 0 \\\ -1 \end{array}\right) = q-2</math>. <br> | ||
| + | (1) Die Gleichung q-2 = 0 hat die Lösung q = 2.<br> | ||
| + | (2) Da in <math>\vec a</math> a<sub>2</sub>=3 ist und bei <math>\vec b</math> b<sub>2</sub>=0 können die Vektoren nicht gegeneinander gerichtet sein. <br> | ||
| + | Rechnerisch führt das zur Gleichung <math>-1 = cos 180^o=\frac{\vec a \circ \vec b}{|\vec a||\vec b|}=\frac{q-2}{\sqrt{q^2+13}\cdot \sqrt 2} </math>, also <math>-\sqrt{q^2+13}\cdot \sqrt 2 = q-2</math> oder <math>\sqrt {2q^2+26}=2-q</math>.<br> | ||
| + | Quadriert man die letze Gleichung , dann erhält man <math>2q^2+26 = q^2-4q+4</math> und in der üblichen Form einer quadratischen Gleichung <math> q^2 +4q+22=0</math>, deren Diskriminante D = -84, also negativ ist. Die quadratische Gleichung hat also keine Lösung. <br> | ||
| + | b) (1) q = 3, (2) <math>q = -\frac{5}{3}</math> (Hier nicht rechnen, sondern die Koordinaten vergleichen!)<br> | ||
| + | c) (1) q = 2 , (2) keine Lösung (bei <math>\vec a</math> müsste a<sub>2</sub>=a<sub>3</sub> sein.) | ||
| + | |||
| + | 111/3 a) s = -2<br> | ||
| + | b) s = -4 oder s = 1<br> | ||
| + | c) <math>s_{1,2}=\pm 2</math> | ||
| + | |||
| + | 111/4 Hier geht es nun um die andere Formel für das Skalarprodukt <math>\vec a \circ \vec b = |\vec a||\vec b|cos\varphi</math>.<br> | ||
| + | a) <math>\vec a \circ \vec b = |\vec a||\vec b|cos\varphi =4\cdot 3 \cdot cos(45^o)=6\sqrt 2</math><br> | ||
| + | <math>-\vec a \circ \vec b = -|\vec a||\vec b|cos\varphi =-4\cdot 3 \cdot cos(45^o)=-6\sqrt 2</math> <br> | ||
| + | b) <math>\vec a \circ \vec b = |\vec a||\vec b|cos\varphi =1\cdot 6 \cdot cos(30^o)=3\sqrt 3</math><br> | ||
| + | <math>-\vec a \circ \vec b = -|\vec a||\vec b|cos\varphi =-1\cdot 6 \cdot cos(30^o)=-3\sqrt 3</math> <br> | ||
| + | c) <math>\vec a \circ \vec b = |\vec a||\vec b|cos\varphi =10\cdot 5 \cdot cos(135^o)=-25\sqrt 2</math><br> | ||
| + | <math>-\vec a \circ \vec b = -|\vec a||\vec b|cos\varphi =-10\cdot 5 \cdot cos(135^o)=25\sqrt 2</math> <br> | ||
| + | d) <math>\vec a \circ \vec b = |\vec a||\vec b|cos\varphi =2,5\cdot 4 \cdot cos(72^o)\approx 3,09</math><br> | ||
| + | <math>-\vec a \circ \vec b = -|\vec a||\vec b|cos\varphi =-2,5\cdot 4 \cdot cos(72^o)\approx -3,09</math> <br> }} | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|3|2=Schaue dir das Video an<br> | ||
| + | {{#ev:youtube |5I2UTXCa4uA|350}}<br> | ||
| + | Notiere die Formel für die senkrechte Projektion.<br> | ||
| + | Buch S. 111 / 7 }} | ||
| + | |||
| + | {{Lösung versteckt|1={{Merke|1=Die Formel für die senkrechte Projektion <math>\vec p</math> des Vektors <math>\vec b</math> auf den Vektor <math>\vec a</math> ist <br> | ||
| + | [[Datei:SenkrechteProjektion.jpg]] <math>\vec p =\frac{\vec b \circ \vec a}{\vec a^2}\cdot \vec a</math> | ||
| + | |||
| + | Beachten Sie, dass in Zähler und Nenner des Bruches vor <math>\vec a</math> Zahlen stehen! Insbesondere ist im Nenner <math>\vec a^2 = |\vec a|^2</math>. }} | ||
| + | |||
| + | 111/7a) <math>\vec p = \frac{\vec b \circ \vec a}{\vec a^2}\cdot \vec a = \frac{\left ( \begin{array}{c} 1 \\\ 2 \\\ -2 \end{array}\right) \circ \left ( \begin{array}{c} 7 \\\ 4 \\\ -4 \end{array}\right) }{\left ( \begin{array}{c} 1 \\\ 2 \\\ -2 \end{array}\right) ^2}\cdot \left ( \begin{array}{c} 1 \\\ 2 \\\ -2 \end{array}\right)=\frac{23}{9} \left ( \begin{array}{c} 1 \\\ 2 \\\ -2 \end{array}\right) </math> <br> | ||
| + | b) <math>\vec p = \frac{\vec b \circ \vec a}{\vec a^2}\cdot \vec a = \frac{\left ( \begin{array}{c} 2 \\\ 5 \\\ -14 \end{array}\right) \circ \left ( \begin{array}{c} 2 \\\ 2 \\\ -1 \end{array}\right) }{\left ( \begin{array}{c} 2 \\\ 5 \\\ -14 \end{array}\right) ^2}\cdot \left ( \begin{array}{c} 2 \\\ 5 \\\ -14 \end{array}\right)=\frac{28}{225} \left ( \begin{array}{c} 2 \\\ 5 \\\ -14 \end{array}\right)</math> }} | ||
| + | |||
| + | {{Aufgaben-blau|4|2=Buch S. 111 / 9 }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) Es ist <math>\vec {AB} = \left ( \begin{array}{c} -3 \\\ 2 \end{array}\right), \vec {AC}= \left ( \begin{array}{c} -9 \\\ 1 \end{array}\right), \vec {BC} = \left ( \begin{array}{c} -6 \\\ -1 \end{array}\right)</math> und <math>|\vec {AB}|=\sqrt {13}, |\vec {AC}|=\sqrt {82}, |\vec {BC}|=\sqrt {37}</math><br> | ||
| + | <math>cos \alpha = \frac{\vec {AB} \circ \vec {AC}}{|\vec {AB}||\vec {AC}|} = \frac{29}{\sqrt {13} \cdot \sqrt {82}}\approx 0,8882</math>, also <math>\alpha = 27,35^o</math><br> | ||
| + | <math>cos \beta = \frac{\vec {BA} \circ \vec {BC}}{|\vec {BA}||\vec {BC}|} = \frac{-16}{\sqrt {13} \cdot \sqrt {37}}\approx -0,7295</math>, also <math>\beta = 136,85^o</math><br> | ||
| + | <math>cos \gamma = \frac{\vec {CA} \circ \vec {CB}}{|\vec {CA}||\vec {CB}|} = \frac{53}{\sqrt {82} \cdot \sqrt {37}}\approx 0,9622</math>, also <math>\gamma = 15,80^o</math><br> | ||
| + | Das Dreieck ist stumpfwinklig und seine längste Seite ist [AC] mit <math>|\vec {AC}|=\sqrt {82}</math> | ||
| + | |||
| + | b) Es ist <math>\vec {AB} = \left ( \begin{array}{c} 2 \\\ -2 \\\ 4 \end{array}\right), \vec {AC}= \left ( \begin{array}{c} -3 \\\ 1 \\\ 5 \end{array}\right), \vec {BC} = \left ( \begin{array}{c} -5 \\\ 3 \\\ 1 \end{array}\right)</math> und <math>|\vec {AB}|=\sqrt {24}, |\vec {AC}|=\sqrt {35}, |\vec {BC}|=\sqrt {35}</math><br> | ||
| + | |||
| + | <math>cos \alpha = \frac{\vec {AB} \circ \vec {AC}}{|\vec {AB}||\vec {AC}|} = \frac{12}{\sqrt {24} \cdot \sqrt {35}}\approx 0,4140</math>, also <math>\alpha = 65,54^o</math><br> | ||
| + | <math>cos \beta = \frac{\vec {BA} \circ \vec {BC}}{|\vec {BA}||\vec {BC}|} = \frac{12}{\sqrt {24} \cdot \sqrt {35}}\approx 0,4140</math>, also <math>\beta = 65,54^o</math><br> | ||
| + | <math>cos \gamma = \frac{\vec {CA} \circ \vec {CB}}{|\vec {CA}||\vec {CB}|} = \frac{23}{\sqrt {35} \cdot \sqrt {35}}\approx 0,6571</math>, also <math>\gamma = 48,92^o</math><br> | ||
| + | Das Dreieck ist gleichschenklig-spitzwinklig. Sein Umfang ist <math>u=2\sqrt{35}+2\sqrt 6</math>, sein Flächeninhalt <math>A=\sqrt {174}</math> | ||
| + | |||
| + | c) Es ist <math>\vec {AB} = \left ( \begin{array}{c} 2 \\\ 1\\\ 2 \end{array}\right), \vec {AC}= \left ( \begin{array}{c} 1 \\\ -1 \\\ 4 \end{array}\right), \vec {BC} = \left ( \begin{array}{c} -1 \\\ -2 \\\ 2 \end{array}\right)</math> und <math>|\vec {AB}|=3, |\vec {AC}|=\sqrt {18}, |\vec {BC}|=3</math><br> | ||
| + | |||
| + | <math>cos \alpha = \frac{\vec {AB} \circ \vec {AC}}{|\vec {AB}||\vec {AC}|} = \frac{9}{3 \cdot \sqrt {18}}=\frac{\sqrt 2}{2} </math>, also <math>\alpha =45^o</math><br> | ||
| + | <math>cos \beta = \frac{\vec {BA} \circ \vec {BC}}{|\vec {BA}||\vec {BC}|} = \frac{0}{3 \cdot \sqrt {18}}= 0</math>, also <math>\beta = 90^o</math><br> | ||
| + | <math>cos \gamma = \frac{\vec {CA} \circ \vec {CB}}{|\vec {CA}||\vec {CB}|} = \frac{9}{\sqrt {18} \cdot 3}=\frac{\sqrt 2}{2} </math>, also <math>\gamma = 45^o</math><br> | ||
| + | Das Dreieck ist gleichschenklig-rechtwinklig. Der Flächeninhalt seines Umkreises ist <math>A_{Kreis}=4,5 \pi</math> }} | ||
| + | |||
| + | {{Aufgaben-blau|5|2=Buch S. 112 / 10<br> | ||
| + | Buch S. 112 / 14<br> | ||
| + | Buch S. 113 / 16 <br> | ||
| + | Buch S. 113 / 19 <br> | ||
| + | Buch S. 113 / 20 }} | ||
| + | |||
| + | {{Lösung versteckt|1=Buch S. 112 / 10<br> | ||
| + | Die Vektoren <math>\vec a</math> und <math>\vec b</math> stehen senkrecht aufeinander, d.h. <math>\vec a \circ \vec b = 0</math>. <br> | ||
| + | a) <math>(\vec a + \vec b)^2 =\vec a^2 + 2\vec a \circ \vec b + \vec b^2=|\vec a|^2 + |\vec b|^2=25+144=169</math><br> | ||
| + | b) <math>(\vec a + \vec b) \circ (2\vec a - \vec b)=2\vec a^2-\vec a \circ \vec b+\vec b \circ 2\vec a - \vec b^2= 2 \cdot 25 - 144 =-94</math><br> | ||
| + | c) Eine Hommage an die binomischen Formeln!<br> | ||
| + | <math>(\vec a + \vec b)^2+(\vec a - \vec b)^2+(\vec a + \vec b)(\vec a -a\vec b) = \vec a^2 + 2 \vec a \circ \vec b + \vec b^2 + \vec a^2 - 2 \vec a \circ \vec b + \vec b^2 + \vec a^2 - \vec b^2= 25 + 144 +25 +144 + 25 -144 = 219</math> | ||
| + | |||
| + | |||
| + | Buch S. 112 / 14<br> | ||
| + | Man weiß aus der Mittelstufe, dass der Flächeninhalt eines Parallelogramms A = gh ist. D.h. fälllt man von der Spitze von <math>\vec b</math> das Lot auf <math>\vec a</math> erhält man die Höhe h. <br> | ||
| + | a steht für <math>a=|\vec a|</math> und b für <math>b=|\vec b|</math>. Es ist dann <math>A = ah</math> und h ist <math>h=b sin\alpha</math>, also <math>A=absin\alpha =ab\sqrt {1-cos\alpha^2} =\sqrt {a^2b^2-a^2b^2cos\alpha^2}=\sqrt{|\vec a|^2|\vec b|^2- (\vec a \circ \vec b)^2}</math> q.e.d.<br> | ||
| + | b) <math>A=\sqrt{72\cdot 18 -0}=36</math> (Beachten Sie, dass <math>\vec a</math> und <math>\vec b</math> senkrecht zueinander sind.)<br> | ||
| + | c) <math>\alpha=74,5^o, \beta=60,98^o, \gamma=44,52^o</math>, <math>h_c=\sqrt {13}, A=\frac{3}{2}\sqrt {13}, V=6\sqrt {13}</math> | ||
| + | |||
| + | 112/15 In dieser Aufgabe wird ein bekannter Satz der Mittelstufe mit Vektoren bewiesen. Man soll zeigen, dass der Winkel ACB gleich 90<sup>o</sup> ist. Dies macht man mit dem Skalarprodukt. Wenn das Skalarprodukt der Vektoren <math>\vec {CA}</math> und <math>\vec {CB}</math> gleich 0 ist, dann ist bei C ein rechter Winkel.<br> | ||
| + | Man drückt <math>\vec {CA}</math> und <math>\vec {CB}</math> durch <math>\vec a, \vec b</math> aus. Es ist <math>\vec {CA}=-\vec b - \vec a</math> und <math>\vec {CB} = -\vec b + \vec a</math>. <br> | ||
| + | Man sieht aus der Zeichnung, dass <math>|\vec a|=|\vec b|=r</math> ist.<br> | ||
| + | Das Skalarprodukt ist dann <math>\vec {CA} \circ \vec {CB}=(-\vec b - \vec a)(-\vec b + \vec a)=-(\vec a + \vec b)(\vec a + \vec b) = -(\vec a^2 - \vec b^2)=-(r^2-r^2)=0</math> | ||
| + | |||
| + | Buch S. 113 / 16<br> | ||
| + | A(2;0,0), B(0;2;0), C(0;0;2) und S(0;0;0)<br> | ||
| + | a) siehe Definition des Skalarprodukts <br> | ||
| + | b) <math>V_{Kugel}=\frac{32}{3}\pi , V_{Pyramide}=\frac{4}{3}</math>. Es ist <math>\frac{V_{Pyramide}}{V_{Kugel}}\approx 0,04=4%</math> | ||
| + | |||
| + | 113/19<br> | ||
| + | [[Datei:113-19.jpg]]<br> | ||
| + | Der Winkel ALF bezeichne ich mit <math>\alpha</math>. Es ist <math>cos \alpha = \frac{\vec {LA}\circ \vec {LF}}{|\vec{LA}||\vec {LF}}=\frac{\left ( \begin{array}{c} 0 \\\ -3 \\\ 4 \end{array}\right) \circ \left ( \begin{array}{c} 4 \\\ -3 \\\ 0 \end{array}\right)}{5\cdot 5}=\frac{9}{25}</math> und <math>\alpha = 68,9^o</math><br> | ||
| + | Das Volumen der Pyramide ist <math>V=\frac{1}{3}\cdot \frac{1}{2} \cdot 3 \cdot 4 \cdot 4=8</math> | ||
| + | |||
| + | 113/20<br> | ||
| + | Es ist <math>\vec {AB}=\left ( \begin{array}{c} 2 \\\ -3 \\\ 0 \end{array}\right), \vec {BC_a}=\left ( \begin{array}{c} 0 \\\ 3 \\\ a-2 \end{array}\right), \vec {AC_a}=\left ( \begin{array}{c} 2 \\\ 0 \\\ a-2 \end{array}\right)</math><br> | ||
| + | Es ist <math>\vec {AB} \circ \vec {AC_a}= \left ( \begin{array}{c} 2 \\\ -3 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 2 \\\ 0 \\\ a-2 \end{array}\right) = 4+0+0=4</math>, also ist bei A kein rechter Winkel.<br> | ||
| + | Es ist <math>\vec {BA} \circ \vec {BC_a}=\left ( \begin{array}{c} -2 \\\ 3 \\\ 0 \end{array}\right) \circ \left ( \begin{array}{c} 0 \\\ 3 \\\ a-2 \end{array}\right) = 0+9+0=9</math>, also ist bei B kein rechter Winkel.<br> | ||
| + | Das Dreieck ABC<sub>a</sub> hat bei C<sub>a</sub> den rechten Winkel. Nun sucht man den Wert von a, für den das Skalarprodukt <math>\vec {C_aA} \circ \vec {C_aB}=0</math> ist.<br> | ||
| + | <math>\vec {C_aA} \circ \vec {C_aB}=\left ( \begin{array}{c} -2 \\\ 0 \\\ 2-a \end{array}\right ) \circ \left ( \begin{array}{c} 0 \\\ -3 \\\ 2-a \end{array}\right)=0+0+(2-a)^2=0</math> für <math>a=2</math>.<br> | ||
| + | Der Flächeninhalt des Dreiecks ist <math>A=\frac{1}{2}|\vec {C_2 A}||\vec {C_2 B}|=0,5\cdot 2 \cdot 3=3 </math> und der Umfang ist <math>u=2+3+\sqrt{13}=5+\sqrt {13}</math> | ||
| − | + | Die Grundfläche der Pyramide liegt in einer zur x<sub>1</sub>x<sub>2</sub>-Ebene parallelen Ebene im Abstand 2. Das Volumen der Pyramide ist dann <math>V= \frac{1}{3}\cdot \frac{1}{2}\cdot 2 \cdot 3 \cdot 2 = 2</math><br> | |
| + | __NOCACHE__ | ||
| + | <ggb_applet height="600" width="600" | ||
| + | filename="113-20.ggb" /> | ||
| + | }} | ||
Aktuelle Version vom 1. Februar 2021, 15:16 Uhr
In Physik hat man gelernt, dass Arbeit W das Produkt aus der Kraft F, die in Wegrichtung entlang des Weges s wirkt. Man schreibt dann W = F·s. Was macht man aber, wenn man einen Leiterwagen zieht?
Nach unserer Arbeitsdefinition muss man den Wagen so wie er abgebildet ist nach vorne ziehen. Dazu muss man sich bücken und es ist sehr unbequem. Man wird den Handgriff hochnehmen, aber dann wirkt die Kraft nicht mehr in Wegrichtung sondern ist schräg dazu. Wenn die Zugstange senkrecht nach oben gerichtet ist, kann man den Leiterwagen gar nicht ziehen. Wie macht sich das dann in der Arbeit bemerkbar?
Man löst das, indem man die Kraftkomponente Fs in Wegrichtung betrachtet und damit die Arbeit Arbeit W = Fs·s berechnet.
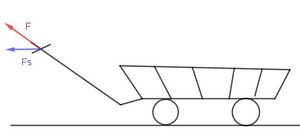
Fs ist die waagrechte Kraftkomponente von F in Fahrtrichtung.
In der Mathematik führt man hierzu das Skalarprodukt ein, dies wird dann in der Physik auch verwendet und man sagt dann, dass die Arbeit W das Skalarprodukt des Kraftvektors 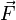 mit dem Wegvektor
mit dem Wegvektor 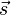 ist, also
ist, also 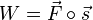 oder ohne Vektoren
oder ohne Vektoren 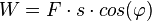 .
.
Beispiele:
1. 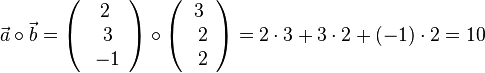 .
.
2. 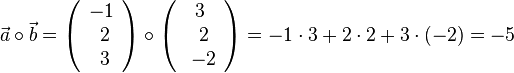 .
.
|
Merke:
Dies führt zur Definition des Winkels. Der Winkel 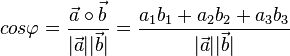
|
Beispiele:
1. 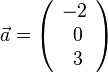 ,
, 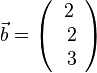 . Es ist
. Es ist 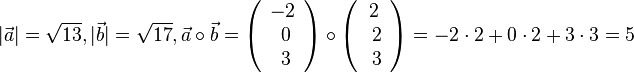 .
.
Damit ist 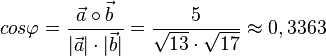 , also
, also 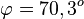
2. 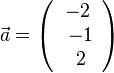 ,
, 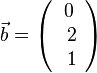 . Es ist
. Es ist 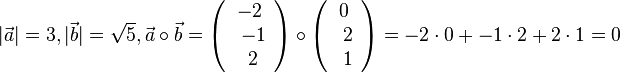 .
.
Damit ist 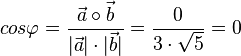 , also
, also 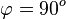 .
.
|
Haben die zwei Vektoren Ist insbesondere
Dies giilt auch umgekehrt. Ist das Skalarprodukt |
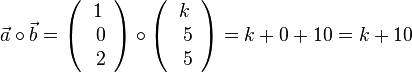 . Es ist k+10 = 0 für k = -10.
. Es ist k+10 = 0 für k = -10.
2. Es ist 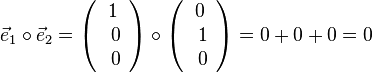 ,
,
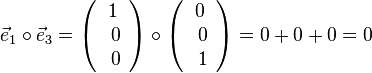 ,
,
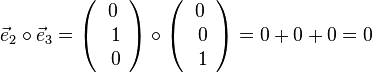
Also sind 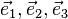 paarweise senkrecht zueinander.
paarweise senkrecht zueinander.
3. Es muss sein: 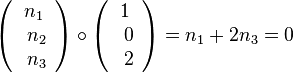 und
und 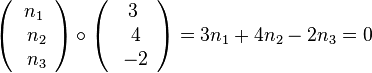
Man hat also zwei Gleichungen 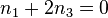 und
und 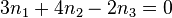 .
.
Löst man die erste Gleichung nach 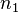 auf, so ist
auf, so ist 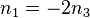 . Dies setzt man in die zweite Gleichung ein und erhält
. Dies setzt man in die zweite Gleichung ein und erhält 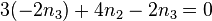 .
.
Dies führt zu der Gleichung 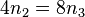 .
.
Wählt man 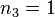 , dann ist
, dann ist 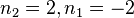 und man hat den Vektor
und man hat den Vektor 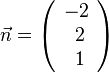 .
.
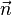 steht senkrecht zu den Vektoren
steht senkrecht zu den Vektoren 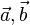 .
.
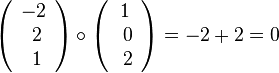 und
und 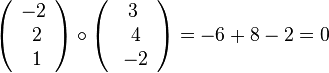
|
Rechengesetze für das Skalarprodukt Für Vektoren
Beachten Sie bitte die unterschiedlichen Malzeichen |
111/1
a) 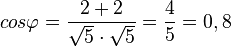 liefert
liefert 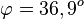
b) 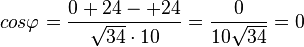 liefert
liefert 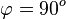
c) 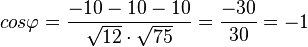 liefert
liefert 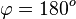
d) 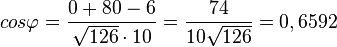 liefert
liefert 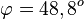
e) 90o
f) 31o
g) 0o
h) 180o
i) 144,7o
111/2 a) 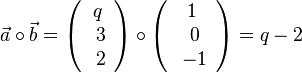 .
.
(1) Die Gleichung q-2 = 0 hat die Lösung q = 2.
(2) Da in  a2=3 ist und bei
a2=3 ist und bei 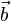 b2=0 können die Vektoren nicht gegeneinander gerichtet sein.
b2=0 können die Vektoren nicht gegeneinander gerichtet sein.
Rechnerisch führt das zur Gleichung 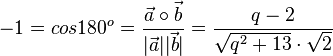 , also
, also 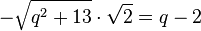 oder
oder 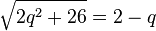 .
.
Quadriert man die letze Gleichung , dann erhält man 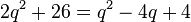 und in der üblichen Form einer quadratischen Gleichung
und in der üblichen Form einer quadratischen Gleichung 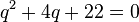 , deren Diskriminante D = -84, also negativ ist. Die quadratische Gleichung hat also keine Lösung.
, deren Diskriminante D = -84, also negativ ist. Die quadratische Gleichung hat also keine Lösung.
b) (1) q = 3, (2) 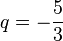 (Hier nicht rechnen, sondern die Koordinaten vergleichen!)
(Hier nicht rechnen, sondern die Koordinaten vergleichen!)
c) (1) q = 2 , (2) keine Lösung (bei  müsste a2=a3 sein.)
müsste a2=a3 sein.)
111/3 a) s = -2
b) s = -4 oder s = 1
c) 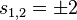
111/4 Hier geht es nun um die andere Formel für das Skalarprodukt 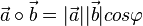 .
.
a) 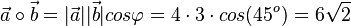
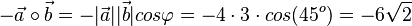
b) 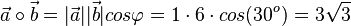
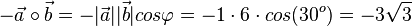
c) 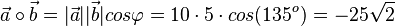
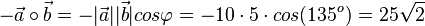
d) 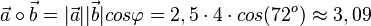
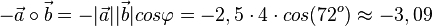
|
Die Formel für die senkrechte Projektion Beachten Sie, dass in Zähler und Nenner des Bruches vor |
111/7a) 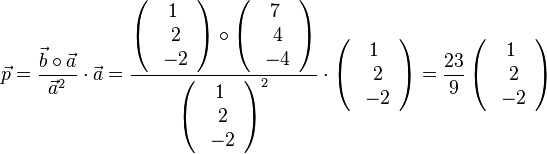
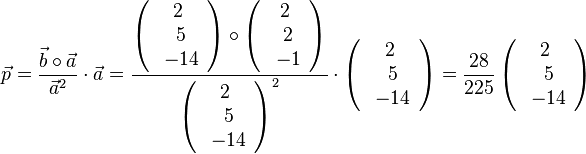
a) Es ist 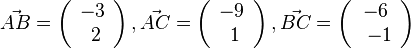 und
und 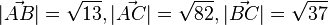
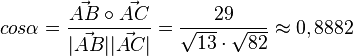 , also
, also 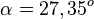
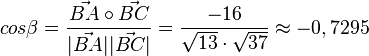 , also
, also 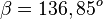
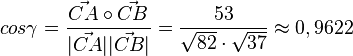 , also
, also 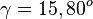
Das Dreieck ist stumpfwinklig und seine längste Seite ist [AC] mit 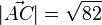
b) Es ist 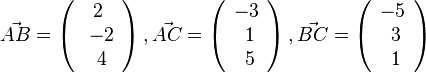 und
und 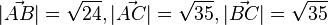
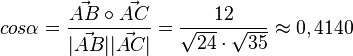 , also
, also 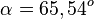
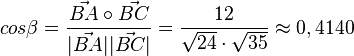 , also
, also 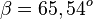
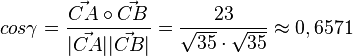 , also
, also 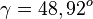
Das Dreieck ist gleichschenklig-spitzwinklig. Sein Umfang ist 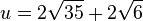 , sein Flächeninhalt
, sein Flächeninhalt 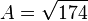
c) Es ist 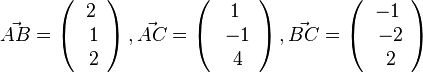 und
und 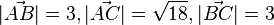
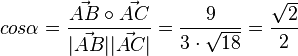 , also
, also 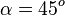
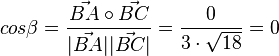 , also
, also 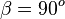
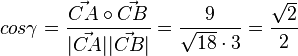 , also
, also 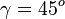
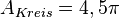
Buch S. 112 / 10
Die Vektoren  und
und 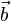 stehen senkrecht aufeinander, d.h.
stehen senkrecht aufeinander, d.h. 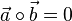 .
.
a) 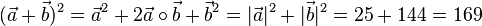
b) 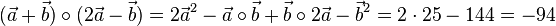
c) Eine Hommage an die binomischen Formeln!
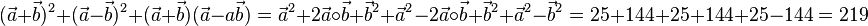
Buch S. 112 / 14
Man weiß aus der Mittelstufe, dass der Flächeninhalt eines Parallelogramms A = gh ist. D.h. fälllt man von der Spitze von 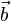 das Lot auf
das Lot auf  erhält man die Höhe h.
erhält man die Höhe h.
a steht für 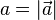 und b für
und b für 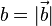 . Es ist dann
. Es ist dann 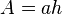 und h ist
und h ist 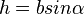 , also
, also 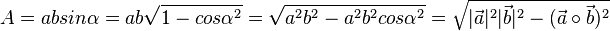 q.e.d.
q.e.d.
b) 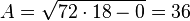 (Beachten Sie, dass
(Beachten Sie, dass  und
und 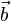 senkrecht zueinander sind.)
senkrecht zueinander sind.)
c) 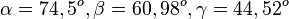 ,
, 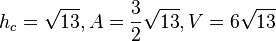
112/15 In dieser Aufgabe wird ein bekannter Satz der Mittelstufe mit Vektoren bewiesen. Man soll zeigen, dass der Winkel ACB gleich 90o ist. Dies macht man mit dem Skalarprodukt. Wenn das Skalarprodukt der Vektoren 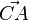 und
und 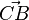 gleich 0 ist, dann ist bei C ein rechter Winkel.
gleich 0 ist, dann ist bei C ein rechter Winkel.
Man drückt 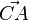 und
und 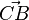 durch
durch 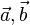 aus. Es ist
aus. Es ist 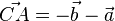 und
und 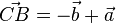 .
.
Man sieht aus der Zeichnung, dass 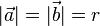 ist.
ist.
Das Skalarprodukt ist dann 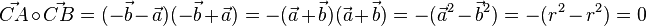
Buch S. 113 / 16
A(2;0,0), B(0;2;0), C(0;0;2) und S(0;0;0)
a) siehe Definition des Skalarprodukts
b) 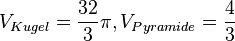 . Es ist
. Es ist 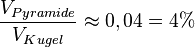
113/19
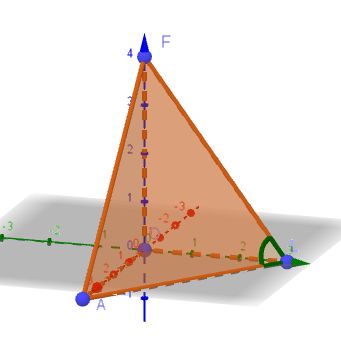
Der Winkel ALF bezeichne ich mit 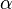 . Es ist
. Es ist 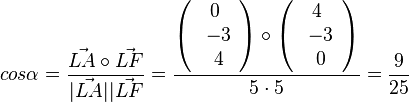 und
und 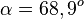
Das Volumen der Pyramide ist 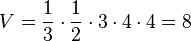
113/20
Es ist 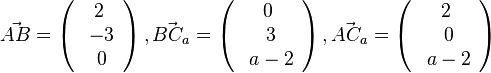
Es ist 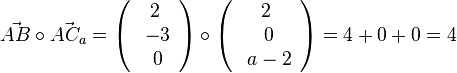 , also ist bei A kein rechter Winkel.
, also ist bei A kein rechter Winkel.
Es ist 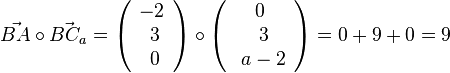 , also ist bei B kein rechter Winkel.
, also ist bei B kein rechter Winkel.
Das Dreieck ABCa hat bei Ca den rechten Winkel. Nun sucht man den Wert von a, für den das Skalarprodukt 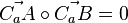 ist.
ist.
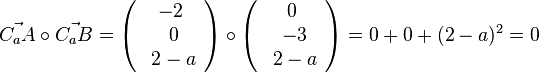 für
für 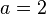 .
.
Der Flächeninhalt des Dreiecks ist 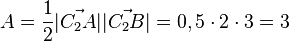 und der Umfang ist
und der Umfang ist 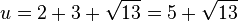
Die Grundfläche der Pyramide liegt in einer zur x1x2-Ebene parallelen Ebene im Abstand 2. Das Volumen der Pyramide ist dann 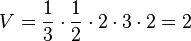


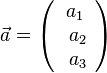 und
und 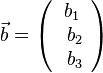 definiert man das Skalarprodukt
definiert man das Skalarprodukt 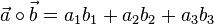 .
.
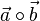 ist eine Zahl (ein Skalar). Es ist
ist eine Zahl (ein Skalar). Es ist 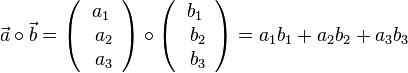 .
.
 , damit man das Multiplizieren von Vektoren vom Multiplizieren von Zahlen unterscheidet.
, damit man das Multiplizieren von Vektoren vom Multiplizieren von Zahlen unterscheidet.
 der Winkel zwischen den Vektoren
der Winkel zwischen den Vektoren 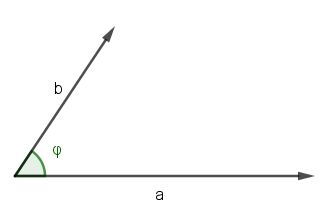
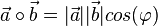
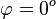 und
und 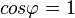 . Dann ist
. Dann ist 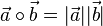 .
.
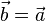 , dann ist
, dann ist 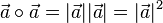 .
. 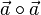 gleich dem Quadrat des Betrags des Vektors
gleich dem Quadrat des Betrags des Vektors 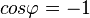 . Dann ist
. Dann ist 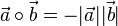 .
.
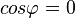 . Damit ist
. Damit ist 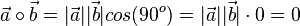 . Die beiden Vektoren
. Die beiden Vektoren 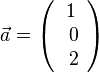 und
und 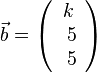 senkrecht zueiander sind.
senkrecht zueiander sind.
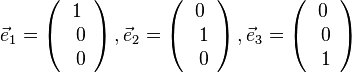 unseres dreidimensionalen Koordinatensystems senkrecht zueinander stehen.
unseres dreidimensionalen Koordinatensystems senkrecht zueinander stehen.
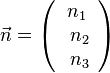 , der senkrecht auf den zwei Vektoren
, der senkrecht auf den zwei Vektoren 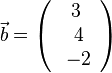 steht.
steht.
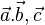 und reelle Zahlen r,s gilt:
und reelle Zahlen r,s gilt: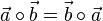
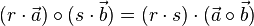
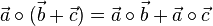
 für Zahlen bzw. S-Multiplikation.
für Zahlen bzw. S-Multiplikation. 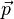 des Vektors
des Vektors 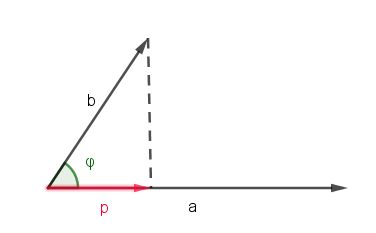
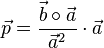
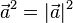 .
.

