M10 Eigenschaften der Exponentialfunktion: Unterschied zwischen den Versionen
Aus RSG-Wiki
(→Zusammenfassung) |
|||
| Zeile 56: | Zeile 56: | ||
* für a > 1 ist der Graph montoton steigend. | * für a > 1 ist der Graph montoton steigend. | ||
| − | * Für 0 < a < 1 nähert sich der Graph beliebig nahe an die positive x-Achse; die positive x-Achse ist Asymptote.<br> | + | * Für 0 < a < 1 nähert sich der Graph beliebig nahe an die positive x-Achse; die positive x-Achse ist '''Asymptote'''.<br> |
| − | * Für a > 1 nähert sich der Graph beliebig nahe an die negative x-Achse; die negative x-Achse ist Asymptote. | + | * Für a > 1 nähert sich der Graph beliebig nahe an die negative x-Achse; die negative x-Achse ist '''Asymptote'''. |
'''b ≠ 1''' | '''b ≠ 1''' | ||
| Zeile 66: | Zeile 66: | ||
* Die Graphen der Funktionen f mit f(x) = b·a<sup>x</sup> und g mit g(x) = -b ·a<sup>x</sup> sind symmetrisch bezüglich der x-Achse. }} | * Die Graphen der Funktionen f mit f(x) = b·a<sup>x</sup> und g mit g(x) = -b ·a<sup>x</sup> sind symmetrisch bezüglich der x-Achse. }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Verifiziere die Aussagen des Merksatzes mit Hilfe des Applets. | ||
| + | |||
| + | <ggb_applet height="600" width="600" | ||
| + | filename="Exponentialfunktion_7.ggb" /> | ||
| + | }} | ||
Version vom 23. Februar 2021, 14:44 Uhr
Inhaltsverzeichnis |
Die Funktion 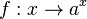
1. Für 0 < a < 1 ist die Exponentialfunktion streng monoton fallend, für a > 1 ist sie streng monoton steigend.
2. Für a = 1 ist die Funktion konstant.
3. Der Graph der Funktion verläuft für alle Werte von a oberhalb der x-Achse.
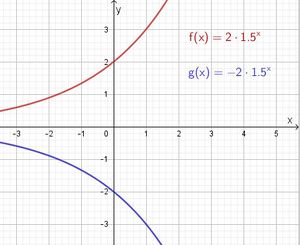
Die Funktion 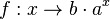
1. Wenn der Faktor b negativ ist, verläuft der Graph der Funktion unterhalb der x-Achse.
Aufgaben
Zusammenfassung

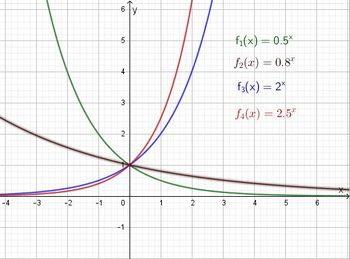
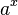 ist stets positiv.
ist stets positiv.
 mit
mit 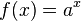 und
und  mit
mit 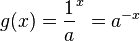 lliegen symmetrisch bezüglich der y-Achse.
lliegen symmetrisch bezüglich der y-Achse.
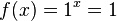 konstant,
konstant,
