M9 Die allgemeine Wurzel: Unterschied zwischen den Versionen
Aus RSG-Wiki
(Die Seite wurde neu angelegt: „Zu Beginn des Schuljahres haben wir <math>\sqrt a</math> als die positive Zahl definiert, die quadriert a ergibt. Diese Definition wird nun erweitert. {{Merk…“) |
|||
| Zeile 2: | Zeile 2: | ||
{{Merksatz|MERK=Die n-te Wurzel <math>\sqrt [n] {a}</math> aus a mit n<math>\in</math>N\{1} und a<math>\in</math>R<sup>+</sup><sub>0</sub> ist diejenige nicht negative reelle Zahl, deren n-te Potenz a ist. | {{Merksatz|MERK=Die n-te Wurzel <math>\sqrt [n] {a}</math> aus a mit n<math>\in</math>N\{1} und a<math>\in</math>R<sup>+</sup><sub>0</sub> ist diejenige nicht negative reelle Zahl, deren n-te Potenz a ist. | ||
| − | <center><math>(\sqrt [n] {a})^n = | + | <center><math>(\sqrt [n] {a})^n = a</math></center> |
}} | }} | ||
Version vom 1. März 2021, 11:00 Uhr
Zu Beginn des Schuljahres haben wir 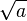 als die positive Zahl definiert, die quadriert a ergibt. Diese Definition wird nun erweitert.
als die positive Zahl definiert, die quadriert a ergibt. Diese Definition wird nun erweitert.
|
Merke:
Die n-te Wurzel ![(\sqrt [n] {a})^n = a](/images/math/3/b/7/3b7a007cfd6f5f5ef3513c35c5bf6032.png) |

![\sqrt [n] {a}](/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) aus a mit n
aus a mit n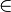 N\{1} und a
N\{1} und a
