M11 Verkettung von Funktionen: Unterschied zwischen den Versionen
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die Funktion <math>f:x \rightarrow \sqrt {x^2+1}</math> ist eine in ganz R definierte Funktion. | Die Funktion <math>f:x \rightarrow \sqrt {x^2+1}</math> ist eine in ganz R definierte Funktion. | ||
<center>[[Datei:Wurzel x^2+1.jpg|500px]]</center> | <center>[[Datei:Wurzel x^2+1.jpg|500px]]</center> | ||
| − | Am Graph sieht man, dass im Punkt (0;1) eine waagrechte Tangente y = 1 vorhanden ist. <br> | + | Am Graph sieht man, dass im Punkt (0;1) eine waagrechte Tangente y = 1 vorhanden ist. Bei x = -20 oder x = -10 ist die Steigung -1 und bei x = 10 und x = 20 ist die Steigung 1. <br> |
Doch wie soll man <math>\sqrt {x^2+1}</math> ableiten?<br> | Doch wie soll man <math>\sqrt {x^2+1}</math> ableiten?<br> | ||
| Zeile 22: | Zeile 22: | ||
| − | {{Merksatz|MERK=Bei der Verkettung <math> u \circ v</math> der Funktionen <math>u</math> und <math> v</math>, die durch <math>u \circ v(x) = u(v(x))</math> gegeben ist, heißt <math>u</math> die '''äußere Funktion''' und <math>v</math> die '''innere Funktion'''. }} | + | {{Merksatz|MERK=Bei der Verkettung <math> u \circ v</math> der Funktionen <math>u</math> und <math> v</math>, die durch <math>u \circ v(x) = u(v(x))</math> gegeben ist, heißt <math>u</math> die '''äußere Funktion''' und <math>v</math> die '''innere Funktion'''. |
| + | |||
| + | Die innere Funktion ist das Argument der äußeren Funktion.}} | ||
| + | |||
| + | |||
| + | Als neue Verknüpfung für die Funktionen <math>f</math> und <math>g</math> wurde die Verkettung <math>f \circ g</math> eingeführt. Dies geht natürlich genauso, dann übernimmt <math>g</math> die Rolle der inneren Funktion und <math>f</math> die Rolle der äußeren Funktion. <br> | ||
| + | Im folgenden Video wird auch die Schreibweise <math>f \circ g</math> dargestellt. | ||
| + | <center>{{#ev:youtube |y7MmgAdibnY|350}}</center> | ||
| Zeile 68: | Zeile 75: | ||
* <math> u(x) = \sqrt x</math> und <math> v(x) = 2(x^2+7)</math> oder<br> | * <math> u(x) = \sqrt x</math> und <math> v(x) = 2(x^2+7)</math> oder<br> | ||
* <math> u(x) = \sqrt {2x}</math> und <math> v(x) = x^2+7</math>. | * <math> u(x) = \sqrt {2x}</math> und <math> v(x) = x^2+7</math>. | ||
| + | |||
| + | <center>{{#ev:youtube |4pn02EvUZx0|350}}</center> | ||
{{Aufgaben-blau|2|2=Buch S. 130 / 2 }} | {{Aufgaben-blau|2|2=Buch S. 130 / 2 }} | ||
| Zeile 83: | Zeile 92: | ||
{{Lösung versteckt|1=Man hat die Funktionen <math>u</math> mit <math> u(x) = \sqrt{x+1}</math> und <math>v</math> mit <math>v(x) = x^2-4</math>. Die Definitionsmenge für <math>u</math> ist D<sub>u</sub> = [-1;<math>\infty</math>[, die Definitionsmenge für <math>v</math> ist D<sub>v</sub> = R.<br> | {{Lösung versteckt|1=Man hat die Funktionen <math>u</math> mit <math> u(x) = \sqrt{x+1}</math> und <math>v</math> mit <math>v(x) = x^2-4</math>. Die Definitionsmenge für <math>u</math> ist D<sub>u</sub> = [-1;<math>\infty</math>[, die Definitionsmenge für <math>v</math> ist D<sub>v</sub> = R.<br> | ||
Die Funktion <math>f</math> mit <math>f(x)=u(v(x))=\sqrt {x^2-4 +1}=\sqrt {x^2-3}</math> hat als Definitionsmenge D<sub>f</sub> = <math>]-\infty;.\sqrt 3]\cup [\sqrt 3;\infty[</math>.<br> | Die Funktion <math>f</math> mit <math>f(x)=u(v(x))=\sqrt {x^2-4 +1}=\sqrt {x^2-3}</math> hat als Definitionsmenge D<sub>f</sub> = <math>]-\infty;.\sqrt 3]\cup [\sqrt 3;\infty[</math>.<br> | ||
| − | Die Funktion <math>g</math> mit <math>g(x)=v(u(x)=(\sqrt {x+1})^2 | + | Die Funktion <math>g</math> mit <math>g(x)=v(u(x)=(\sqrt {x+1})^2-4=x+1-4=x-3</math> hat als Definitionsmenge D<sub>g</sub>=[-1;<math>\infty</math>[. Hierzu muss man beachten, dass man ja x zuerst in u einsetzt. Da darf man nur Zahlen, die größer oder gleich -1 sind einsetzen. Man erhält für u(x) eine Zahl, die größer oder gleich 0 ist. Diese Zahl u(x) wird dann in v eingesetzt. <br> |
Von den Zahlen -2, <math>-\sqrt 3</math>, -1, 0, 1, 2, 3 gehören zur <br> | Von den Zahlen -2, <math>-\sqrt 3</math>, -1, 0, 1, 2, 3 gehören zur <br> | ||
* Definitionsmenge von f die Zahlen -2, <math>-\sqrt 3</math>, 2, 3. <br> | * Definitionsmenge von f die Zahlen -2, <math>-\sqrt 3</math>, 2, 3. <br> | ||
* Definitionsmenge von G die Zahlen -1, 0, 1, 2, 3. }} | * Definitionsmenge von G die Zahlen -1, 0, 1, 2, 3. }} | ||
Aktuelle Version vom 1. März 2021, 13:48 Uhr
Die Funktion 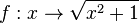 ist eine in ganz R definierte Funktion.
ist eine in ganz R definierte Funktion.
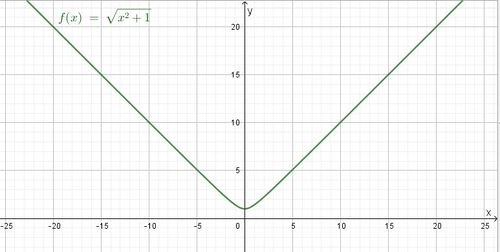
Am Graph sieht man, dass im Punkt (0;1) eine waagrechte Tangente y = 1 vorhanden ist. Bei x = -20 oder x = -10 ist die Steigung -1 und bei x = 10 und x = 20 ist die Steigung 1.
Doch wie soll man 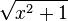 ableiten?
ableiten?
Dazu müssen wir die Verknüpfung zweier Funktionen um die Verkettung erweitern. Bisher kennen wir als Verknüpfung zweier Funktiongen f und g
- die Summe f + g
- die Differenz f - g
- die Multiplikation f · g und
- die Division
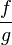
Nun kommt noch die Verkettung 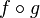 dazu.
dazu.
|
Merke:
Bei der Verkettung (Hintereinanderausführung) |
Für unser Beispiel 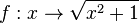 betrachten wir die Funktionen
betrachten wir die Funktionen 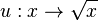 und
und 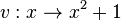 . Es ist
. Es ist 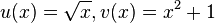 .
.
Setzt man nun 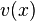 an die Stelle von
an die Stelle von 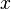 in der Funktion
in der Funktion  , dann hat man
, dann hat man 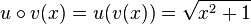 und
und  ist die Verkettung
ist die Verkettung 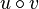 der Funktionen
der Funktionen  und
und  , also
, also 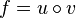 .
.
|
Merke:
Bei der Verkettung Die innere Funktion ist das Argument der äußeren Funktion. |
Als neue Verknüpfung für die Funktionen  und
und  wurde die Verkettung
wurde die Verkettung 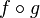 eingeführt. Dies geht natürlich genauso, dann übernimmt
eingeführt. Dies geht natürlich genauso, dann übernimmt  die Rolle der inneren Funktion und
die Rolle der inneren Funktion und  die Rolle der äußeren Funktion.
die Rolle der äußeren Funktion.
Im folgenden Video wird auch die Schreibweise 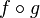 dargestellt.
dargestellt.
Beispiele: 1. Für die Funktionen  mit
mit 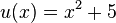 und
und  mit
mit 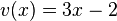 ist
ist
-
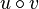 durch
durch 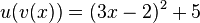 gegeben. (In der Funktion u ersetzt man x durch den Term von v(x).)
gegeben. (In der Funktion u ersetzt man x durch den Term von v(x).)
-
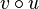 durch
durch 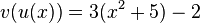 . (In der Funktion v ersetzt man x durch den Term von u(x).)
. (In der Funktion v ersetzt man x durch den Term von u(x).)
Natürlich vereinfacht man noch die Terme. Es ist dann 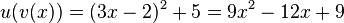 und
und 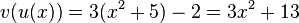 .
.
Insbesondere sieht man, dass die Verkettung nicht kommutativ ist. 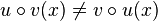 .
.
2. Für die Funktionen  mit
mit 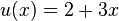 und
und  mit
mit 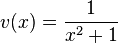 ist
ist
-
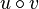 durch
durch 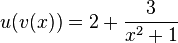 gegeben. (In der Funktion u ersetzt man x durch den Term von v(x).)
gegeben. (In der Funktion u ersetzt man x durch den Term von v(x).)
-
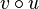 durch
durch 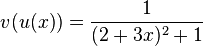 . (In der Funktion v ersetzt man x durch den Term von u(x).)
. (In der Funktion v ersetzt man x durch den Term von u(x).)
3. Für die Funktionen  mit
mit 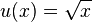 und
und  mit
mit 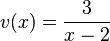 ist
ist
-
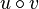 durch
durch 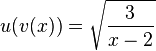 gegeben.
gegeben.
-
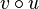 durch
durch 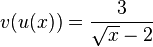 .
.
a) 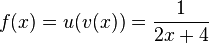 und
und 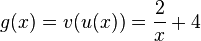
b) ![f(x) = u(v(x))=cos[(x+1)^2]](/images/math/b/e/4/be44141b323c7b684584573c60714290.png) und
und 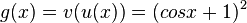
c) 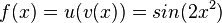 und
und ![g(x)=v(u(x))=[sin(2x)]^2](/images/math/6/5/a/65a43ed2da1cd7ac46565340695f3048.png)
d) 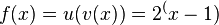 und
und 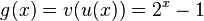
e) 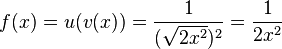 und
und 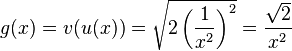
f) 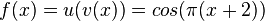 und
und 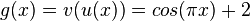
g) 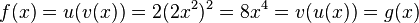
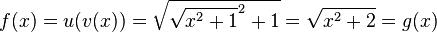
Oftmals kann man auch eine Funktion  als Verkettung zweier Funktionen
als Verkettung zweier Funktionen  und
und  schreiben.
schreiben.
1. Die Funktion  mit
mit 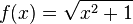 ist die Verkettung
ist die Verkettung 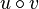 mit den Funktionen
mit den Funktionen
 mit
mit 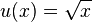 und
und  mit
mit 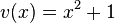 .
.
2. 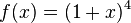 ist
ist 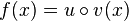 mit
mit 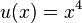 und
und 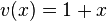 .
.
3. 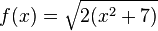 ist
ist 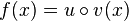 mit
mit
-
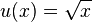 und
und 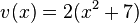 oder
oder
-
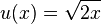 und
und 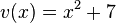 .
.
Es ist 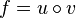 mit
mit
a)  mit
mit 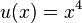 und
und  mit
mit 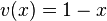
b)  mit
mit 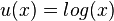 und
und  mit
mit 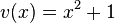
c)  mit
mit 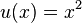 und
und  mit
mit 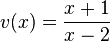
 mit
mit 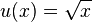 und
und  mit
mit 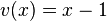
Man hat die Funktionen  mit
mit 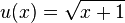 und
und  mit
mit 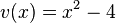 . Die Definitionsmenge für
. Die Definitionsmenge für  ist Du = [-1;
ist Du = [-1; [, die Definitionsmenge für
[, die Definitionsmenge für  ist Dv = R.
ist Dv = R.
Die Funktion  mit
mit 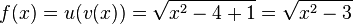 hat als Definitionsmenge Df =
hat als Definitionsmenge Df = ![]-\infty;.\sqrt 3]\cup [\sqrt 3;\infty[](/images/math/f/8/f/f8f584044fd183cbf059458e5de9c470.png) .
.
Die Funktion  mit
mit 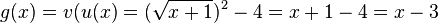 hat als Definitionsmenge Dg=[-1;
hat als Definitionsmenge Dg=[-1; [. Hierzu muss man beachten, dass man ja x zuerst in u einsetzt. Da darf man nur Zahlen, die größer oder gleich -1 sind einsetzen. Man erhält für u(x) eine Zahl, die größer oder gleich 0 ist. Diese Zahl u(x) wird dann in v eingesetzt.
[. Hierzu muss man beachten, dass man ja x zuerst in u einsetzt. Da darf man nur Zahlen, die größer oder gleich -1 sind einsetzen. Man erhält für u(x) eine Zahl, die größer oder gleich 0 ist. Diese Zahl u(x) wird dann in v eingesetzt.
Von den Zahlen -2, 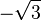 , -1, 0, 1, 2, 3 gehören zur
, -1, 0, 1, 2, 3 gehören zur
- Definitionsmenge von f die Zahlen -2,
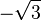 , 2, 3.
, 2, 3.
- Definitionsmenge von G die Zahlen -1, 0, 1, 2, 3.

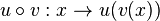 .
.
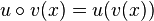 gegeben ist, heißt
gegeben ist, heißt 
