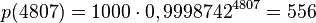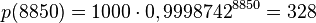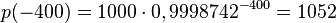M11 Funktionsgleichungen der Exponentialfunktion: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „Hier geht es darum aus einem Sachzusammenhang eine Funktionsgleichung einer Exponentialfunktion zu erstellen und die Aufgabe damit zu lösen. Es geht um Expone…“) |
|||
| Zeile 8: | Zeile 8: | ||
1. <math>830\cdot 10^6 = b\cdot a^0</math>, wenn man im Jahr 2000 mit der Zeitrechnung beginnt. Also ist hier <math>b = 830\cdot 10^6</math> und <br> | 1. <math>830\cdot 10^6 = b\cdot a^0</math>, wenn man im Jahr 2000 mit der Zeitrechnung beginnt. Also ist hier <math>b = 830\cdot 10^6</math> und <br> | ||
2. <math> 898\cdot 10^6=830\cdot 10^6 \cdot a^5</math> <br> | 2. <math> 898\cdot 10^6=830\cdot 10^6 \cdot a^5</math> <br> | ||
| − | Die letzte Gleichung führt zu <math>898 = 830 \cdot a^5</math> und <math>a = \sqrt [5] {\frac{ | + | Die letzte Gleichung führt zu <math>898 = 830 \cdot a^5</math> und <math>a = \sqrt [5] {\frac{449}{415}}\approx 1,016</math><br> |
| + | Der jährliche Wachstumsfaktor ist a = 1,016. Die Bevölkerung nimmt jährlich um 1,6% zu.<br> | ||
| + | Das Wachstumsgesetz lautet <math>f(x)= 830 \cdot 10^6 \cdot 1,016^x</math>. | ||
| + | |||
| + | b) <math>f(25)= 830 \cdot 10^6 \cdot 1,016^{25}=1234\cdot 10^6</math>, <math>f(50)= 830 \cdot 10^6 \cdot 1,016^{50}=1836\cdot 10^6</math> | ||
}} | }} | ||
{{Aufgaben-blau|2|2=Buch S. 97 / 15 }} | {{Aufgaben-blau|2|2=Buch S. 97 / 15 }} | ||
| − | {{Lösung versteckt|1= }} | + | {{Lösung versteckt|1=a) Bei einer exponentiellen Abnahme nimmt die Konzentration anfangs stark ab und am Ende wenig. Daher wirkt es am Anfang stärker und die Wirkung nimmt gegen Ende ab. |
| + | |||
| + | b) Ansatz: <math>c(t)=b\cdot a^{t}</math>. Es ist <math>c(3)=8,4</math> und <math>c(8) = 6,3</math>. Man hat also zwei Gleichungen:<br> | ||
| + | (1) <math>8,4 = b\cdot a^{3}</math> und<br> | ||
| + | (2) <math>6,3 = b\cdot a^{8}</math> <br> | ||
| + | Dividiert man die Gleichungen (1):(2) erhält man <math>\frac{8,4}{6,3}=a^{^-5}</math> und <math>a = \sqrt [5]{\frac{6,3}{8,4}} =\sqrt [5]{0,75}\approx 0,944</math>. <br> | ||
| + | Die Anfangskonzentration b erhält man, indem man den Wert von a in eine der Gleichungen einsetzt und nach b auflöst.<br> | ||
| + | <math>8,4=b \cdot 0,944^3</math> ergibt <math>b = 9,985</math>. Also war die Anfangskonzentration etwa 10 mg/l.<br> | ||
| + | Die Abnahme pro Stunde ist 0,056 = 5,6%. | ||
| + | |||
| + | c) <math>c(12)=10\cdot 0,994^{12}=5,0</math> und <math>c(24)=10 \cdot 0,994^{24}=2,5</math> | ||
| + | |||
| + | d) Tabletten sollten nach Vorschrift eingenommen werden um eine möglichst hohe Wirksamkeit zu erzielen. | ||
| + | |||
| + | Bemerkung: Man hätte auch einen Ansatz <math>c(t)=b\cdot a^{-t}</math> in b) machen können, dann wäre a = 1,06. Die Abnahme wird durch das - im Exponenten berücksichtigt. }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Buch S. 97 / 16 }} | ||
| + | |||
| + | {{Lösung versteckt|1=Ansatz <math>p(h)=b\cdot a^h</math><br> | ||
| + | a) Man setzt die Werte ein und erhält zwei Gleichungen<br> | ||
| + | (1) <math>915 = b\cdot a^{708}</math> und <br> | ||
| + | (2) <math> 689 = b \cdot a^{2963}</math><br> | ||
| + | Dividiert man (2):(1) erhält man <math>\frac{689}{915}=a^{2255}</math> und <math>a = \sqrt [2255]{\frac{689}{915}}=0,9998742</math><br> | ||
| + | <math>915 = b \cdot 0,9998742^{708}</math> ergibt <math>b=1000</math>.<br> | ||
| + | Die Luftdruckformel ist <math>p(h)=1000\cdot 0,9998742^h</math>.<br> | ||
| + | In Meereshöhe (h = 0) ist der Luftdruck 1000 hPa.<br> | ||
| + | Pro 1 km nimmt der Luftdruck um 11,8% ab. | ||
| + | |||
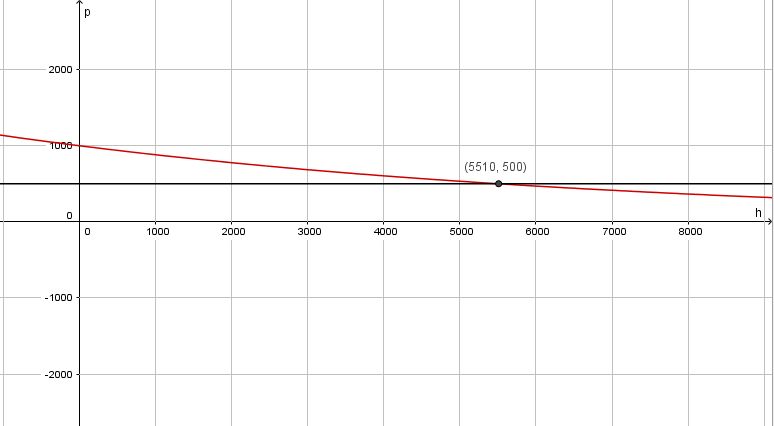
| + | b) [[Datei:97-16.jpg]] | ||
| + | |||
| + | c) Bei <math>\Delta</math>h = 5510 m halbiert sich jeweils der Luftdruck. | ||
| − | {{ | + | d) <math>p(4807)=1000\cdot 0,9998742^{4807}=556</math><br> |
| + | <math>p(8850)=1000\cdot 0,9998742^{8850}=328</math><br> | ||
| + | <math>p(-400)=1000\cdot 0,9998742^{-400}=1052</math> }} | ||
Version vom 3. März 2021, 14:54 Uhr
Hier geht es darum aus einem Sachzusammenhang eine Funktionsgleichung einer Exponentialfunktion zu erstellen und die Aufgabe damit zu lösen. Es geht um Exponentialfunktionen mit der Funktionsgleichung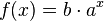 
.
Man hat zwei Angaben mit denen man zwei Gleichungen erhält und dann a und b berechnet.
Im Jahr 2000 war die Bevölkerung 830 Millionen, 2005, also 5 Jahre später war die Bevölkerung 898 Millionen.
Das führt zu den zwei Gleichungen
1. 
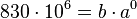, wenn man im Jahr 2000 mit der Zeitrechnung beginnt. Also ist hier 
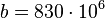und
2. 
Die letzte Gleichung führt zu 
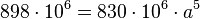
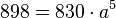und ![a = \sqrt [5] {\frac{449}{415}}\approx 1,016](/images/math/a/2/c/a2cc1a79b808b870caeace7c18afaf6f.png)
Der jährliche Wachstumsfaktor ist a = 1,016. Die Bevölkerung nimmt jährlich um 1,6% zu.
Das Wachstumsgesetz lautet 
.
, 
a) Bei einer exponentiellen Abnahme nimmt die Konzentration anfangs stark ab und am Ende wenig. Daher wirkt es am Anfang stärker und die Wirkung nimmt gegen Ende ab.
b) Ansatz: 
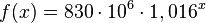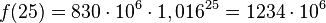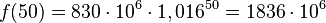
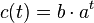. Es ist 
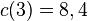und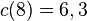 
. Man hat also zwei Gleichungen:
(1) 
und
(2) 
Dividiert man die Gleichungen (1):(2) erhält man 
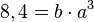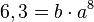
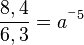und ![a = \sqrt [5]{\frac{6,3}{8,4}} =\sqrt [5]{0,75}\approx 0,944](/images/math/0/7/1/071b1100c2034322621db0f414417ecb.png)
.
Die Anfangskonzentration b erhält man, indem man den Wert von a in eine der Gleichungen einsetzt und nach b auflöst.
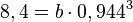ergibt 
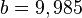. Also war die Anfangskonzentration etwa 10 mg/l.
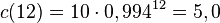Die Abnahme pro Stunde ist 0,056 = 5,6%.
c) 
und 
d) Tabletten sollten nach Vorschrift eingenommen werden um eine möglichst hohe Wirksamkeit zu erzielen.
Bemerkung: Man hätte auch einen Ansatz
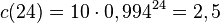
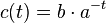in b) machen können, dann wäre a = 1,06. Die Abnahme wird durch das - im Exponenten berücksichtigt.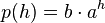
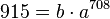Ansatz 
a) Man setzt die Werte ein und erhält zwei Gleichungen
(1) 
und
(2) 
Dividiert man (2):(1) erhält man 
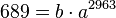
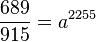und ![a = \sqrt [2255]{\frac{689}{915}}=0,9998742](/images/math/9/8/5/98596db12aa8392d9c07551f9d879ec5.png)
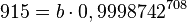ergibt 
.
Die Luftdruckformel ist 
.
In Meereshöhe (h = 0) ist der Luftdruck 1000 hPa.
Pro 1 km nimmt der Luftdruck um 11,8% ab.
b) 
c) Bei 
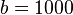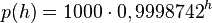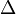h = 5510 m halbiert sich jeweils der Luftdruck.
d) 
