Hefteintrag: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „<div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1E1FF; align:left;">'''Hefteintrag''' 1. Den Graphen der Funktion f…“) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1E1FF; align:left;">'''Hefteintrag''' | <div style="margin:0; border:2px solid #dfdfdf; padding: 0em 1em 1em 1em; background-color:#F1E1FF; align:left;">'''Hefteintrag''' | ||
| − | 1 | + | =Definition= |
| + | {{Merke|1= | ||
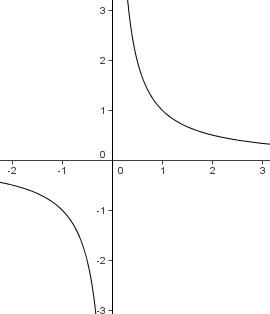
| + | Den Graphen der Funktion f mit y = 1/x bezeichnet man als '''Hyperbel''' oder Ur-Hyperbel. | ||
[[bild:1-x.jpg|center]] | [[bild:1-x.jpg|center]] | ||
| + | }} | ||
| − | + | =Parameter a= | |
| + | |||
| + | {{Merke|1= | ||
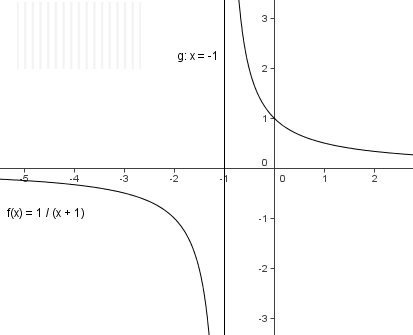
| + | Der Graph der Funktion f mit y = 1/(x+a) ist ebenfalls eine Hyperbel. Er entspricht dem Graph der Ur-Hyperbel, verschoben um den Wert a nach links. <br> | ||
[[bild:1-(x-a).jpg|center]] | [[bild:1-(x-a).jpg|center]] | ||
Beachte: Für x=-a ist die Funktion nicht definiert. | Beachte: Für x=-a ist die Funktion nicht definiert. | ||
| + | }} | ||
| − | + | In diesem Applet kannst du a mit dem Schieberegler variieren. | |
| + | <ggb_applet height="500" width="700" | ||
| + | filename="1-(x-a).ggb" /><br> | ||
| + | |||
| + | {{Merke|1= | ||
Für die x-Werte größer als -a gilt, je mehr sich x an -a annähert, desto größer wird y.<br> | Für die x-Werte größer als -a gilt, je mehr sich x an -a annähert, desto größer wird y.<br> | ||
Für die x-Werte kleiner als -a gilt, je mehr sich x an -a annähert, desto kleiner wird y.<br> | Für die x-Werte kleiner als -a gilt, je mehr sich x an -a annähert, desto kleiner wird y.<br> | ||
Die Gerade x = -a ist '''vertikale Asymptote'''. | Die Gerade x = -a ist '''vertikale Asymptote'''. | ||
| + | }} | ||
| − | + | =Parameter b= | |
| + | {{Merke|1= | ||
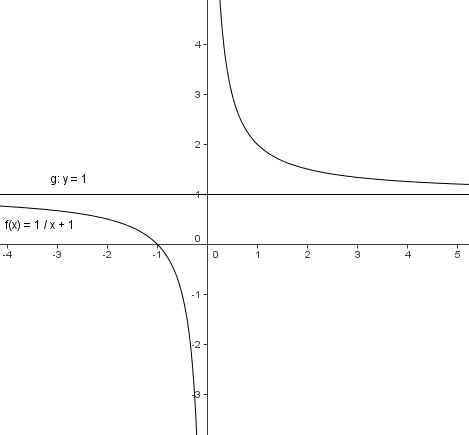
| + | Der Graph der Funktion y = 1/x +b ist ebenfalls eine Hyperbel. Er entspricht dem Graph der Orthogonal-Hyperbel, verschoben um den Wert b nach oben. <br> | ||
[[bild:1-x -b.jpg|center]] | [[bild:1-x -b.jpg|center]] | ||
Beachte: Für x=0 ist die Funktion nicht definiert. | Beachte: Für x=0 ist die Funktion nicht definiert. | ||
| + | }} | ||
| − | + | In diesem Applet kannst du b mit dem Schieberegler variieren: | |
| + | <ggb_applet height="500" width="700" | ||
| + | filename="1-x_-b.ggb" /> <br> | ||
| + | |||
| + | {{Merke|1= | ||
Für die x-Werte sehr viel größer als 0 gilt, je größer x wird, desto mehr nähert sich y an b an.<br> | Für die x-Werte sehr viel größer als 0 gilt, je größer x wird, desto mehr nähert sich y an b an.<br> | ||
Für die x-Werte sehr viel kleiner als 0 gilt, je kleiner x wird, desto mehr nähert sich y an b an.<br> | Für die x-Werte sehr viel kleiner als 0 gilt, je kleiner x wird, desto mehr nähert sich y an b an.<br> | ||
Die Gerade y = b ist '''horizontale Asymptote'''. | Die Gerade y = b ist '''horizontale Asymptote'''. | ||
| + | }} | ||
| − | + | =Parameter a und b= | |
| + | |||
| + | {{Merke|1= | ||
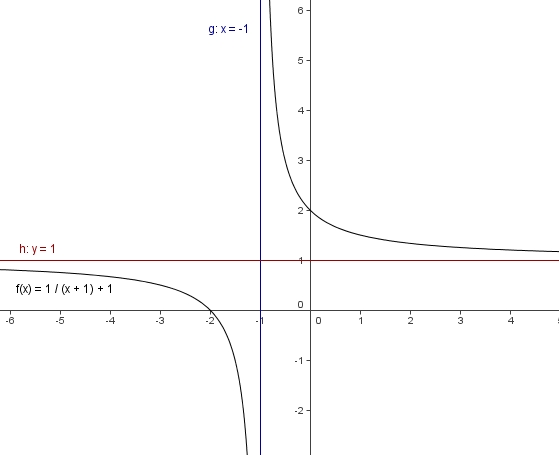
| + | Der Graph der Funktion f mit y = c/(x+a) +b ist ebenfalls eine Hyperbel.<br> | ||
Er entspricht dem Graphen der Ur-Hyperbel, verschoben <br> | Er entspricht dem Graphen der Ur-Hyperbel, verschoben <br> | ||
um den Wert a nach links und um den Wert b nach oben.<br> | um den Wert a nach links und um den Wert b nach oben.<br> | ||
[[Bild:1-(x-a)-b.jpg|center]] | [[Bild:1-(x-a)-b.jpg|center]] | ||
| − | Für x = -a ist die Funktion nicht definiert. | + | Für x = -a ist die Funktion nicht definiert. |
| − | + | }} | |
| + | In diesem Applet kannst du die drei Parameter a, b, c mit Schiebereglern variieren: | ||
| + | |||
| + | <ggb_applet height="500" width="700" | ||
| + | filename="1-(x-a)-b.ggb" /><br> | ||
| + | {{Merke|1= | ||
Der Graph hat die Gerade x = -a als vertikale Asymptote und y = b als horizontale Asymptote. | Der Graph hat die Gerade x = -a als vertikale Asymptote und y = b als horizontale Asymptote. | ||
| + | }} | ||
</div> | </div> | ||
---- | ---- | ||
[[Rationale Funktionen/Lernpfad|Zurück]] | [[Rationale Funktionen/Lernpfad|Zurück]] | ||
Aktuelle Version vom 30. April 2011, 14:42 Uhr
Inhaltsverzeichnis |
Definition
30px Merke
Den Graphen der Funktion f mit y = 1/x bezeichnet man als Hyperbel oder Ur-Hyperbel. |
Parameter a
30px Merke
Der Graph der Funktion f mit y = 1/(x+a) ist ebenfalls eine Hyperbel. Er entspricht dem Graph der Ur-Hyperbel, verschoben um den Wert a nach links. Beachte: Für x=-a ist die Funktion nicht definiert. |
In diesem Applet kannst du a mit dem Schieberegler variieren.
30px Merke
Für die x-Werte größer als -a gilt, je mehr sich x an -a annähert, desto größer wird y. |
Parameter b
30px Merke
Der Graph der Funktion y = 1/x +b ist ebenfalls eine Hyperbel. Er entspricht dem Graph der Orthogonal-Hyperbel, verschoben um den Wert b nach oben. Beachte: Für x=0 ist die Funktion nicht definiert. |
In diesem Applet kannst du b mit dem Schieberegler variieren:
30px Merke
Für die x-Werte sehr viel größer als 0 gilt, je größer x wird, desto mehr nähert sich y an b an. |
Parameter a und b
30px Merke
Der Graph der Funktion f mit y = c/(x+a) +b ist ebenfalls eine Hyperbel. Für x = -a ist die Funktion nicht definiert. |
In diesem Applet kannst du die drei Parameter a, b, c mit Schiebereglern variieren:
30px Merke
Der Graph hat die Gerade x = -a als vertikale Asymptote und y = b als horizontale Asymptote. |