M9 Die allgemeine Wurzel: Unterschied zwischen den Versionen
| Zeile 80: | Zeile 80: | ||
D = <math>R_0^+</math> und ...= 17b | D = <math>R_0^+</math> und ...= 17b | ||
| − | c) D = <math>R_0^+</math> | + | c) D = <math>R_0^+</math><br> |
| − | + | <math>\sqrt [4]{625\cdot g^2\cdot (g^3)^2}</math> <br> | |
| − | D = <math>R_0^+</math> und | + | Hier fasst man zuerst den Radikand zusammen es ist <math>g^2 \cdot (g^3)^2=g^2\cdot g^6=g^{2+6}=g^8</math> und <math> 625 = 5^4</math>. Damit formt man um <math>\sqrt [4]{625\cdot g^2\cdot (g^3)^2}=\sqrt [4]{5^4\cdot g^8}=\sqrt [4]{5^4\cdot (g^2)^4}=5\cdot g^2</math> |
| − | D = <math>R_0^+</math> und | + | |
| + | |||
| + | D = <math>R^+</math><br> | ||
| + | <math>\sqrt [3]{\frac{h^7}{0,001\cdot h}}=\sqrt [3] {\frac{h^6}{\frac{1}{1000}}}=\sqrt [3]{1000\cdot h^6}=\sqrt [3]{10^3\cdot (h^2)^3}=10\cdot h^2</math> | ||
| + | |||
| + | |||
| + | D = <math>R_0^+</math> und<br> | ||
| + | Hier fasst man zuerst die k's im Radikand zusammen:<br> | ||
| + | <math>\sqrt [5]{\frac{k^{2n+3}}{0,00032\cdot k^n\cdot k^{-2}}}=\sqrt [5]{0,2^5\cdot k^{2n+3-n-(-2)}}=\sqrt [5]{0,2^5\cdot k^{n+5}}=\sqrt [5]{0,2^5 \cdot k^{5(0,2n+1)}}=0,2\cdot k^{0,2n+1}</math> | ||
| + | |||
| + | |||
| + | D = <math>R_0^+</math> und <br> | ||
| + | <math>\sqrt [3]{1728\cdot b^6}=\sqrt [3] {12^3 \cdot (b^2)^3}=12\cdot b^2</math> | ||
| + | |||
111/4 a) <math>x^3 = - 125</math> --> <math>x = -5</math>, L = {-5}<br> | 111/4 a) <math>x^3 = - 125</math> --> <math>x = -5</math>, L = {-5}<br> | ||
b) <math>x^6 = - 32</math> --> L = { }<br> | b) <math>x^6 = - 32</math> --> L = { }<br> | ||
c) <math>x^2 = 8</math> --> <math>x =\pm 2\sqrt 2</math>, L = {<math>-2\sqrt2;2\sqrt2</math>}<br> | c) <math>x^2 = 8</math> --> <math>x =\pm 2\sqrt 2</math>, L = {<math>-2\sqrt2;2\sqrt2</math>}<br> | ||
| − | d) | + | d) Multipliziert man die Gleichung mit <math>x^3</math>, dann erhält man <math>x^4 = 8</math> --> <math>x =\pm \sqrt [4]{8}</math>, L = {<math>-\sqrt [4]{8};\sqrt [4]{8}</math>}<br> |
e) <math>x^4 = 81</math> --> <math>x = \pm 3</math>, L = {-3,3}<br> | e) <math>x^4 = 81</math> --> <math>x = \pm 3</math>, L = {-3,3}<br> | ||
f) <math>x^5 = 0</math> --> <math>x = 0</math>, L = {0}<br> }} | f) <math>x^5 = 0</math> --> <math>x = 0</math>, L = {0}<br> }} | ||
Version vom 11. März 2021, 12:57 Uhr
Zu Beginn des Schuljahres haben wir 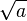 als die positive Zahl definiert, die quadriert a ergibt. Diese Definition wird nun erweitert.
als die positive Zahl definiert, die quadriert a ergibt. Diese Definition wird nun erweitert.
|
Merke:
Die n-te Wurzel ![(\sqrt [n] {a})^n = a](/images/math/3/b/7/3b7a007cfd6f5f5ef3513c35c5bf6032.png) Die Zahl a unter dem Wurzelzeichen heißt Radikand, n ist der Wurzelexponent. Es ist 1. Für |
Beispiele: ![\sqrt [5] {1024} = 4](/images/math/c/d/f/cdf9e10220895ffd78969ffd1c45d2f4.png) Tipp: Mache die Umkehrrechnung
Tipp: Mache die Umkehrrechnung 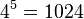 !
!
![\sqrt [4] {0,0016} = 0,2](/images/math/b/f/3/bf3a40d532633f46620db7e11aeae85a.png)
![\sqrt [10] {1024} = 2](/images/math/d/e/b/deb29ea68afda2936fc6b5202e5ba1cb.png)
![\sqrt [3] {216} = 6](/images/math/b/b/b/bbb8d86b8dfcb8c9b861eddb3a8bd42f.png)
![\sqrt [5] {243} = 3](/images/math/e/0/5/e05396213ebba89eaebcb52448c6f6cd.png)
![\sqrt [3] {729} = 9](/images/math/a/2/8/a285934a9163e49c806a2513a126965b.png)
Wenn a < 0 ist, dann hat die quadratische Gleichung x2 = a keine Lösung. Wenn nun n eine ungerade Zahl ist, dann gibt es Lösungen. Die Gleichung x3 = -8 hat die Lösung x = -2, da (-2)3 = -8 ist. Also kann man unterscheiden:
30px Merke
Die Gleichung xn = a kann zwei Lösungen, eine Lösung oder keine Lösung haben, je nachdem ob: n gerade ist und n ungerade ist und |
Mit der n-ten Wurzel hat man die Möglichkeit weitere Gleichungen zu lösen:
x3 = 216 hat die Lösung x = 6
x3 = -216 hat die Lösung x = -6
x5 = 1024 hat die Lösung x = 4
x4 = 256 hat die Lösungen x = -4 und x = 4
x4 = 2401 hat die Lösungen x = -7 und x = 7
x5 = -243 hat die Lösung x = -3
x4 = -256 hat die keine Lösung
Für die kommenden Aufgaben sind die Potenzgesetze hilfreich.
30px Merke
Es ist |
111/3 a) D = 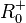 und ...= a2
und ...= a2
D = 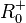 und ...= b3
und ...= b3
D = 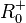 und ...=
und ...= ![c^{\frac{1}{3}} = \sqrt [3]{c}](/images/math/2/c/e/2ce5874bcf5ef5c13bb3c13f89c54626.png)
D = 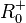 und ...= 3·b2
und ...= 3·b2
b) D = 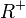 und ...= d-1
und ...= d-1
D = 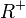 und ...= e-2
und ...= e-2
D = 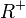 und ...= f-2
und ...= f-2
D = 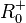 und ...= 17b
und ...= 17b
c) D = 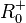
![\sqrt [4]{625\cdot g^2\cdot (g^3)^2}](/images/math/0/f/8/0f87e5be71bb9486e6f7cce61654b373.png)
Hier fasst man zuerst den Radikand zusammen es ist 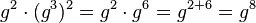 und
und 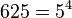 . Damit formt man um
. Damit formt man um ![\sqrt [4]{625\cdot g^2\cdot (g^3)^2}=\sqrt [4]{5^4\cdot g^8}=\sqrt [4]{5^4\cdot (g^2)^4}=5\cdot g^2](/images/math/6/9/a/69a0928d24b6444825d30120f4eef471.png)
D = 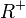
![\sqrt [3]{\frac{h^7}{0,001\cdot h}}=\sqrt [3] {\frac{h^6}{\frac{1}{1000}}}=\sqrt [3]{1000\cdot h^6}=\sqrt [3]{10^3\cdot (h^2)^3}=10\cdot h^2](/images/math/e/0/b/e0bf459ed66513cbc39d788fe64aa827.png)
D = 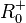 und
und
Hier fasst man zuerst die k's im Radikand zusammen:
![\sqrt [5]{\frac{k^{2n+3}}{0,00032\cdot k^n\cdot k^{-2}}}=\sqrt [5]{0,2^5\cdot k^{2n+3-n-(-2)}}=\sqrt [5]{0,2^5\cdot k^{n+5}}=\sqrt [5]{0,2^5 \cdot k^{5(0,2n+1)}}=0,2\cdot k^{0,2n+1}](/images/math/7/f/2/7f21d303917010978e435e4109521dd3.png)
D = 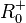 und
und
![\sqrt [3]{1728\cdot b^6}=\sqrt [3] {12^3 \cdot (b^2)^3}=12\cdot b^2](/images/math/3/7/8/3788b37a03c528fc3b3abae1be09373d.png)
111/4 a) 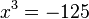 -->
--> 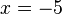 , L = {-5}
, L = {-5}
b) 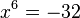 --> L = { }
--> L = { }
c) 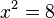 -->
--> 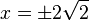 , L = {
, L = {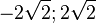 }
}
d) Multipliziert man die Gleichung mit 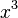 , dann erhält man
, dann erhält man 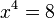 -->
--> ![x =\pm \sqrt [4]{8}](/images/math/5/6/9/569755fe8c96f848be08ef81f8a11374.png) , L = {
, L = {![-\sqrt [4]{8};\sqrt [4]{8}](/images/math/8/2/6/826c9d601497b6a1b8e9d8581276e1ff.png) }
}
e) 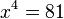 -->
--> 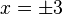 , L = {-3,3}
, L = {-3,3}
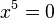 -->
--> 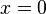 , L = {0}
, L = {0}
V = 216 dm3 entspricht einem Würfel mit Seitenlänge s = 6 dm.
Der Oberflächeninhalt ist O = 6·36 dm2=216 dm2.

![\sqrt [n] {a}](/images/math/9/a/2/9a2b6d33f3d62a1e8bd99c76f3cb79f5.png) aus a mit n
aus a mit n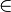 N\{1} und a
N\{1} und a![\sqrt [n] {a} \ge 0](/images/math/b/e/f/befde518159cf76e5392a4a14345374a.png)
![\sqrt [n] {a^n} = a](/images/math/a/7/3/a73d367ed0ace076492bd5d360b13ed6.png) falls a ≥ 0
falls a ≥ 0
![\sqrt [n] {a} = a^{\frac{1}{n}}](/images/math/e/c/8/ec88827417db352f94755f7f655c012e.png) .
.
![-\sqrt [n] {a}, \sqrt [n] {a}](/images/math/9/1/f/91f0181839fadbec49ab7cf78f53f424.png) }
}![-\sqrt [n]{-a}](/images/math/2/b/b/2bb6203d113a9afd39ab62b8955960ba.png) } (Wenn a < 0 ist, dann ist -a > 0!)
} (Wenn a < 0 ist, dann ist -a > 0!)
 ;
;  ; 2;
; 2; 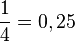 ; 1,5
; 1,5

![\sqrt [n]{a^n} = a = (\sqrt [n]{a})^n](/images/math/7/e/5/7e50e1b6f7efba24f2add51189ce855a.png) .
.

