M11 Der Wahrscheinlichkeitsbegriff: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
Eine Funktion P, die jeder Teilmenge E einer Ergebnismenge <math>\Omega</math> eine reelle Zahle P(E) zuordnet heißt Wahrscheinlichkeitsfunktion oder Wahrschlichkeitsverteilung, wenn die drei Bedingungen erfüllt sind: | Eine Funktion P, die jeder Teilmenge E einer Ergebnismenge <math>\Omega</math> eine reelle Zahle P(E) zuordnet heißt Wahrscheinlichkeitsfunktion oder Wahrschlichkeitsverteilung, wenn die drei Bedingungen erfüllt sind: | ||
| − | 1. <math>P(E) \ge 0</math> | + | 1. <math>P(E) \ge 0</math> (Nichtnegativität) |
| − | 2. <math>P(\Omega) = 1</math> | + | 2. <math>P(\Omega) = 1</math> (Normiertheit) |
| − | 3. <math> P(E_1 \cup E_2) = P(E_1)+P(E_2)</math>, wenn <math>E_1\cap E_2 = \lbrace \rbrace</math> }} | + | 3. <math> P(E_1 \cup E_2) = P(E_1)+P(E_2)</math> (Additivität), wenn <math>E_1\cap E_2 = \lbrace \rbrace</math> |
| + | |||
| + | <center>{{#ev:youtube |GtpN4SRESaA|350}} </center> }} | ||
Man sieht, dass die Axiome von Kolmogorow sich sehr stark an die Eigenschaften der Laplace-Wahrscheinlichkeiten anlehnen. Nur geht es hier um die geforderten Eigenschaften einer Wahrscheinlichkeitsfunktion P, die hiermit jedem Ereignis eine Wahrscheinlichkeit P(E) zuordnet. Die Funktion P muss diese drei Axiome erfüllen, dann ist sie eine Wahrscheinlichkeitsfunktion. | Man sieht, dass die Axiome von Kolmogorow sich sehr stark an die Eigenschaften der Laplace-Wahrscheinlichkeiten anlehnen. Nur geht es hier um die geforderten Eigenschaften einer Wahrscheinlichkeitsfunktion P, die hiermit jedem Ereignis eine Wahrscheinlichkeit P(E) zuordnet. Die Funktion P muss diese drei Axiome erfüllen, dann ist sie eine Wahrscheinlichkeitsfunktion. | ||
Beispiele: 1. Werfen eines Laplace-Würfels<br> | Beispiele: 1. Werfen eines Laplace-Würfels<br> | ||
| + | <center>{{#ev:youtube |OyPLqgdMJ6I|350}} </center> | ||
Die Wahrscheinlichkeiten beim Laplace-Würfel für die möglichen Ergebnisse 1, 2, 3, 4, 5, 6 sind jeweils <math>P(\lbrace 1 \rbrace)= P(\lbrace 2 \rbrace)=P(\lbrace 3 \rbrace)=P(\lbrace 4 \rbrace)=P(\lbrace 5 \rbrace)=P(\lbrace 6 \rbrace)=\frac{1}{6}</math><br> | Die Wahrscheinlichkeiten beim Laplace-Würfel für die möglichen Ergebnisse 1, 2, 3, 4, 5, 6 sind jeweils <math>P(\lbrace 1 \rbrace)= P(\lbrace 2 \rbrace)=P(\lbrace 3 \rbrace)=P(\lbrace 4 \rbrace)=P(\lbrace 5 \rbrace)=P(\lbrace 6 \rbrace)=\frac{1}{6}</math><br> | ||
Die Axiome von Kolmogorow sind erfüllt:<br> | Die Axiome von Kolmogorow sind erfüllt:<br> | ||
| Zeile 62: | Zeile 65: | ||
<center><math>P(A\cup B)=P(A) + P(B) - P(A\cap B)</math> </center> }} | <center><math>P(A\cup B)=P(A) + P(B) - P(A\cap B)</math> </center> }} | ||
| + | |||
| + | {{Aufgaben-blau|1|2=<math>A</math> ist ein Ereignis aus <math>\Omega</math>. Zeigen Sie, dass für sein Gegenereignis <math>\overline A</math> gilt: | ||
| + | <center><math>P(\overline {A}) = 1 - P(A)</math></center> }} | ||
| + | |||
| + | {{Lösung versteckt|1=<math>A</math> und <math>\overline A</math> sind unvereinbare Ereignisse. Es ist <math>A \cap \overline A =\lbrace \rbrace</math>. Weiter ist <math>A \cup \overline A = \Omega</math>.<br> | ||
| + | Für die Wahrscheinlichkeiten gilt dann <math> P(A) + P(B) = P(A \cup B)=P(ẞOmega) = 1</math>. <br> | ||
| + | Damit ist <math>P(A) + P(\overline A)=1</math> und <math> P(\overline {A}) = 1 - P(A)</math>. }} | ||
| + | |||
| + | {{Aufgaben-blau|2|2=Bearbeiten Sie [http://www.raschweb.de/M11-Kolmogorow.pdf dies Arbeitsblatt]. }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Gegeben sind der Ergebnisraum <math>\Omega = \lbrace \omega_1, \omega_2, \omega_3 \omega_4 \rbrace</math>, die Ereignisse <math>E_1=\lbrace \omega_1, \omega_2 \rbrace, E_2=\lbrace \omega_3 \rbrace, E_3=\lbrace \omega_4 \rbrace</math> und die Wahrscheinlichkeiten <math>P(E_1)=0,2, P(E_3) = 0,5=P(E_4)</math>. | ||
| + | |||
| + | a) Zeigen Sie, dass P keine Wahrscheinlichkeitsfunktion ist. <br> | ||
| + | b) Ändern sie <math>P(E_3)</math> so ab, dass eine Wahrscheinlichkeitsfunktion für P entsteht und berechnen Sie dann die Wahrscheinlichkeiten für die Elementarereignisse <math>\lbrace \omega_i </rbrace</math> unter der Voraussetzung, dass \math>\omega_1</math> viermal so wahrscheinlich ist als <math>\omega_2</math>. }} | ||
| + | |||
| + | {{Lösung versteckt|1=a)Es ist <math>P(\Omega)=\P(\omega_1)+P(\omega_2)+P(\omega_3)+P(\omega_4)=0,2+0,5+0,5\ne 1</math>. | ||
| + | |||
| + | b) }} | ||
Version vom 25. April 2021, 17:08 Uhr
Ein wichtiger Begriff bei Berechnungen ist die Laplace-Wahrscheinlichkeit. Laplace führte bei gleichwahrscheinlichen Ergebnissen die Wahrscheinlichkeit eines Ereignisses E aals
Anzahl der für E günstigen Ergebnisse
P(E)= ---------------------------------------
Anzahl aller Ergebnisse
Als Eigenschaften der Laplace-Wahrscheinlichkeit erhält man:
1. 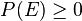
2. 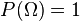
3. Sind zwei Ereignisse A und B unvereinbar 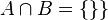 , dann ist
, dann ist 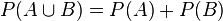 .
.
30px Merke
Zwei Ereignisse Ereignisse A und B heißen unvereinbar, wenn |
Über 200 Jahre später definierte Kolmogorow Wahrscheinlichkeiten über seine Axiome zur Wahrscheinlichkeitsfunktion.
|
Merke:
Axiomensystem von Kolmogorow Eine Funktion P, die jeder Teilmenge E einer Ergebnismenge 1. 2. 3. |
Man sieht, dass die Axiome von Kolmogorow sich sehr stark an die Eigenschaften der Laplace-Wahrscheinlichkeiten anlehnen. Nur geht es hier um die geforderten Eigenschaften einer Wahrscheinlichkeitsfunktion P, die hiermit jedem Ereignis eine Wahrscheinlichkeit P(E) zuordnet. Die Funktion P muss diese drei Axiome erfüllen, dann ist sie eine Wahrscheinlichkeitsfunktion.
Beispiele: 1. Werfen eines Laplace-Würfels
Die Wahrscheinlichkeiten beim Laplace-Würfel für die möglichen Ergebnisse 1, 2, 3, 4, 5, 6 sind jeweils 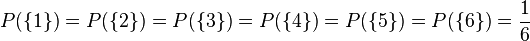
Die Axiome von Kolmogorow sind erfüllt:
1. 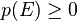
2. 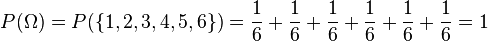
3. Die Ergebnisse sind unvereinbare Ereignisse, es gilt hier die Summenformel.
Also hat man eine Wahrscheinlichkeitsfunktion P, die jedem Ergebnis (Elementarereignis) die Wahrscheinlichkeit  zuordnet.
zuordnet.
2. Werfen eines "gezinkten" Würfels
Man hat einen Würfel mit den Augenzahlen 1,2,3,4,5,6 und 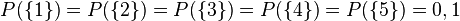 und
und 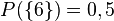
Auch hier sind die Axiome von Kolmogorw erfüllt:
1. 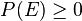
2. 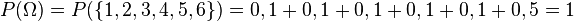
3. Die Ergebnisse sind unvereinbare Ereignisse, es gilt hier die Summenformel.
3. Werfen eines "exotischen Würfels"
Man hat einen Würfel mit den Augenzahlen 1,2,3,4,5,6 und 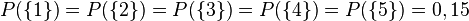 und
und 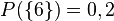
Hier ist das 2. Axiom von Kolmogorw nicht erfüllt:
2. 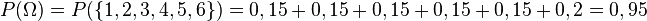
P ist keine Wahrscheinlichkeitsfunktion. Diesen Würfel gibt es nicht!
Was macht man, wenn 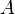 und
und 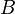 nicht unvereinbar sind?
nicht unvereinbar sind?
Das Ereignisdiagramm schaut dann so aus:
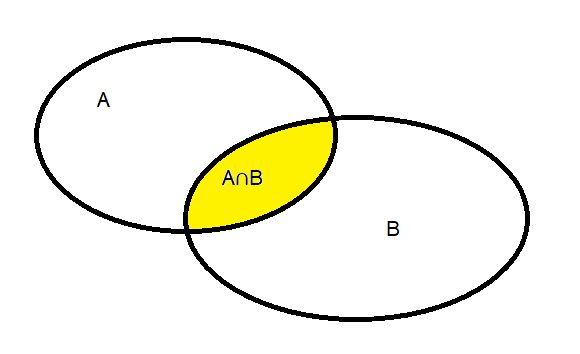
Hier sieht man, dass in der Schnittmenge 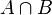 alle Elemente sind, die sowohl in
alle Elemente sind, die sowohl in 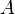 als auch in
als auch in 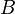 vorkommen. In der Vereinigungsmenge
vorkommen. In der Vereinigungsmenge 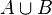 werden diese Elemente für P(A) und P(B) jeweils gezählt, sie werden doppelt gezählt. Um dies zu korrigieren, muss man die Elemente der Schnittmenge einmal abziehen.
werden diese Elemente für P(A) und P(B) jeweils gezählt, sie werden doppelt gezählt. Um dies zu korrigieren, muss man die Elemente der Schnittmenge einmal abziehen.
30px Merke
Für Ereignisse A und B, die nicht unvereinbar sind ( 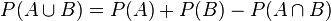 |
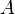 und
und 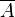 sind unvereinbare Ereignisse. Es ist
sind unvereinbare Ereignisse. Es ist 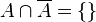 . Weiter ist
. Weiter ist 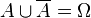 .
.
Für die Wahrscheinlichkeiten gilt dann Fehler beim Parsen(Lexikalischer Fehler): P(A) + P(B) = P(A \cup B)=P(ẞOmega) = 1
.
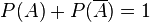 und
und 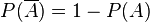 .
.
a)Es ist 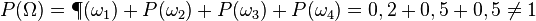 .
.
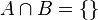 ist.
ist.

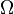 eine reelle Zahle P(E) zuordnet heißt Wahrscheinlichkeitsfunktion oder Wahrschlichkeitsverteilung, wenn die drei Bedingungen erfüllt sind:
eine reelle Zahle P(E) zuordnet heißt Wahrscheinlichkeitsfunktion oder Wahrschlichkeitsverteilung, wenn die drei Bedingungen erfüllt sind:
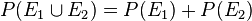 (Additivität), wenn
(Additivität), wenn 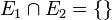
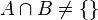 ) gilt:
) gilt:
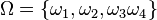 , die Ereignisse
, die Ereignisse 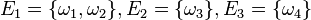 und die Wahrscheinlichkeiten
und die Wahrscheinlichkeiten 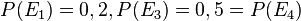 .
.
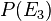 so ab, dass eine Wahrscheinlichkeitsfunktion für P entsteht und berechnen Sie dann die Wahrscheinlichkeiten für die Elementarereignisse
so ab, dass eine Wahrscheinlichkeitsfunktion für P entsteht und berechnen Sie dann die Wahrscheinlichkeiten für die Elementarereignisse 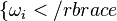 unter der Voraussetzung, dass \math>\omega_1</math> viermal so wahrscheinlich ist als
unter der Voraussetzung, dass \math>\omega_1</math> viermal so wahrscheinlich ist als 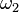 .
.

