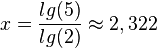M10 Exponentialgleichungen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{Merksatz|MERK=Eine Gleichung, bei der die Unbekannte x nur im Exponenten vorkommt heißt '''Exponentialgleichung'''. }} Zum Lösen einer Exponentialgleichu…“) |
|||
| Zeile 12: | Zeile 12: | ||
Diese Gleichung löst man nach x auf <math>x = \frac{lg(2)}{lg(1,035)}\approx 20,149</math> | Diese Gleichung löst man nach x auf <math>x = \frac{lg(2)}{lg(1,035)}\approx 20,149</math> | ||
| − | {{Aufgaben-blau||2=Löse die Exponentialgleichung. | + | {{Aufgaben-blau||2=Löse die Exponentialgleichung. Runde gegebenenfalls auf 3 Nachkommastellen. |
a) <math>5\cdot 1,06^x = 15</math> | a) <math>5\cdot 1,06^x = 15</math> | ||
| Zeile 38: | Zeile 38: | ||
m) <math>2^x + \left ( \frac{1}{2} \right )^{-x} = 12,5</math> | m) <math>2^x + \left ( \frac{1}{2} \right )^{-x} = 12,5</math> | ||
| − | o) <math>2^x | + | o) <math>2^x - 5\left ( \frac{1}{2} \right )^x = 4</math> }} |
| − | {{Lösung versteckt|1=a) <math>lg(5\cdot 1,06^x) = lg(15)</math><br> | + | {{Lösung versteckt|1=a) <math>5\cdot 1,06^x = 15</math><br> |
| + | <math>lg(5\cdot 1,06^x) = lg(15)</math><br> | ||
<math>lg(5) + lg(1,06^x) = lg(15)</math><br> | <math>lg(5) + lg(1,06^x) = lg(15)</math><br> | ||
<math>x\cdot lg(1,06) = lg(15) - lg(5)</math><br> | <math>x\cdot lg(1,06) = lg(15) - lg(5)</math><br> | ||
| Zeile 66: | Zeile 67: | ||
-------------------------------------------------- | -------------------------------------------------- | ||
| − | e) | + | e) <math>2^x\cdot 5^{-x} = 6,25</math><br> |
| − | }} | + | <math>2^x\cdot 0,2^x = 6,25</math><br> |
| + | <math>0,4^x = 6,25</math><br> | ||
| + | <math>x\cdot lg(0,4)=lg(6,25)</math> | ||
| + | <math>x = \frac{lg(6,25)}{lg(0,4}=-2</math> | ||
| + | |||
| + | -------------------------------------------------- | ||
| + | f) <math>2^x = 3^{2x}</math><br> | ||
| + | <math>x\cdot lg(2)=2x\cdot lg(3)</math><br> | ||
| + | <math>x(lg(2)-2lg(3))=0</math><br> | ||
| + | <math> x = 0</math> | ||
| + | |||
| + | ------------------------------------------------- | ||
| + | g) <math>2^{x-1} = 3</math><br> | ||
| + | <math>(x-1)lg(2) = lg(3)</math><br> | ||
| + | <math>x = \frac{lg(3)}{lg(2)}+1\approx 2,285</math> | ||
| + | |||
| + | ------------------------------------------------- | ||
| + | h) <math>0,25^{1-x}=10,25</math><br> | ||
| + | <math>(1-x)lg(0,25)=lg(10,25)</math><br> | ||
| + | <math>x = 1-\frac{lg(10,25)}{lg(0,25)}\approx 2,679</math> | ||
| + | |||
| + | -------------------------------------------------- | ||
| + | i) <math>10\cdot 25^{x+3} = 2</math><br> | ||
| + | <math>1+(x+3)lg(25)=lg(2)</math><br> | ||
| + | <math>x = \frac{lg(2)-1}{lg(25)}-3=-3,5</math> | ||
| + | |||
| + | ------------------------------------------------- | ||
| + | k) <math>2^x + 2^3 = 10,25</math><br> | ||
| + | <math>2^x = 2,25</math><br> | ||
| + | <math>x \approx 1,170</math> | ||
| + | |||
| + | ----------------------------------------------- | ||
| + | l) <math>5\cdot 9^x + \left ( \frac{1}{3} \right ) ^{-2} = 7</math><br> | ||
| + | <math>5\cdot 9^x =7-9</math><br> | ||
| + | <math>5 \cdot 9^x = -1</math> hat keine Lösung! | ||
| + | |||
| + | -------------------------------------------------- | ||
| + | m) <math>2^x + \left ( \frac{1}{2} \right )^{-x} = 12,5</math><br> | ||
| + | <math>2^x + 2^x = 12,5</math><br> | ||
| + | <math>2\cdot 2^x = 12,5</math><br> | ||
| + | <math>2^x = 6,25</math><br> | ||
| + | <math>x = \frac{lg(6.25)}{lg(2)}\approx 2,644</math> | ||
| + | |||
| + | -------------------------------------------------- | ||
| + | o) <math>2^x - 5\left ( \frac{1}{2} \right )^x = 4</math> <br> | ||
| + | <math>(2^x)^2 - 5 = 4\cdot 2^x</math><br> | ||
| + | <math>(2^x)^2 - 4\cdot 2^x - 5 = 0</math><br> | ||
| + | Substituiere <math>z = 2^x</math><br> | ||
| + | <math>z^2 - 4z - 5 = 0</math><br> | ||
| + | <math>(z+1)(z-5)=0</math><br> | ||
| + | <math>z_1=-1, z_2 = 5</math><br> | ||
| + | Zurücksubstituieren:<br> | ||
| + | <math>2^{x_1}=-1</math> geht nicht!, <math>2^{x_2}=5</math> ergibt <math>x=\frac{lg(5)}{lg(2)}\approx 2,322</math> }} | ||
Version vom 28. April 2021, 13:15 Uhr
|
Merke:
Eine Gleichung, bei der die Unbekannte x nur im Exponenten vorkommt heißt Exponentialgleichung. |
Zum Lösen einer Exponentialgleichung bildet man von beiden Seiten den Zehnerlogarithmus und löst diese neue Gleichung
unter Verwendung des Potenzgesetzes für Logarithmen.
Man kann eigentlich jeden Logarithmus zu irgendeiner Basis verwenden. Der Zehnerlogarithmus ist auf Taschenrechnern als Taste dabei und damit leicht verwendbar. Da auf dem Taschenrechner auch eine ln-Taste für den Logarithmus zur Basis e vorhanden ist, könnte man auch den ln nehmen. Allerdings wissen wir noch nichts über die Zahl e, die hier dann Basis ist.
Beispiel: 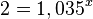
Man bildet auf beiden Seiten den Zehnerlogarithmus 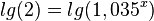
.
Nun wendet man auf der rechten Seite das Potenzgesetz an: 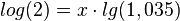 .
.
Diese Gleichung löst man nach x auf 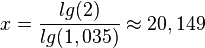
a) 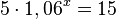
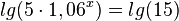
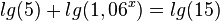
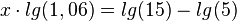
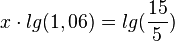
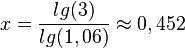
b) 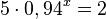
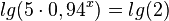
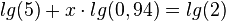
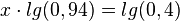
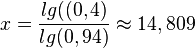
c) 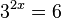
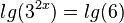
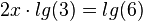
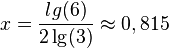
d) 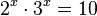
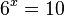
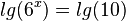
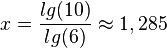
e) 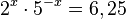
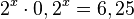
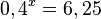
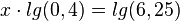
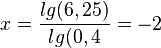
f) 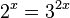
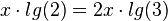
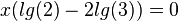
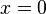
g) 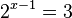
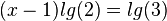
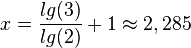
h) 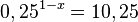
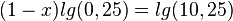
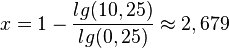
i) 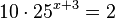
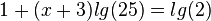
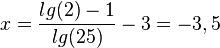
k) 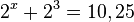
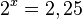
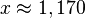
l) 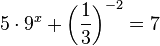
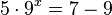
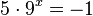 hat keine Lösung!
hat keine Lösung!
m) 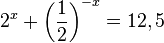
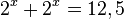
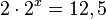
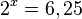
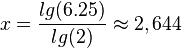
o) 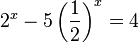
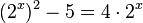
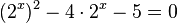
Substituiere 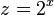
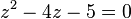
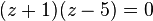
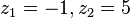
Zurücksubstituieren:
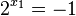 geht nicht!,
geht nicht!, 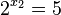 ergibt
ergibt