Ph9 Aufnahme und Abgabe von Energie: Unterschied zwischen den Versionen
| Zeile 47: | Zeile 47: | ||
| Spektrum einer | | Spektrum einer | ||
|- | |- | ||
| − | | Quecksilberdampflampe || Natriumdampflmape | + | | Quecksilberdampflampe || Natriumdampflmape || Wasserstoff |
|- | |- | ||
| − | | [[Datei:Hg-Spektrum.jpg|200px]] || [[Datei:Na-D-sodium_D-lines-589nm.jpg|200px]] | + | | [[Datei:Hg-Spektrum.jpg|200px]] || [[Datei:Na-D-sodium_D-lines-589nm.jpg|200px]] ||[[Datei:Visible_spectrum_of_hydrogen.jpg|300px]] |
|} | |} | ||
| Zeile 69: | Zeile 69: | ||
Das Elektron bleibt aber nicht auf der Bahn m = 3. Es will wieder auf eine Bahn niedrigerer Energie wechseln. Von der Bahn m = 3 kann es auf die Bahn mit m = 2 heruntergehen. Dabei gibt es die Energie <math>\Delta</math>E = 12,09eV - 10,2eV in Form eines Photons ab, das wir als Licht wahrnehmen. Nach einer kurzen Zeit geht es weiter in seinen Grundzustand m = 1 und gibt dabei die Energiedifferenz dieser beiden Bahnen <math>\Delta</math>E=10,2eV - 0eV wieder als Photon ab. Allerdings sehen wir dieses Photon nicht, da es im UV-Bereich ist. <br> | Das Elektron bleibt aber nicht auf der Bahn m = 3. Es will wieder auf eine Bahn niedrigerer Energie wechseln. Von der Bahn m = 3 kann es auf die Bahn mit m = 2 heruntergehen. Dabei gibt es die Energie <math>\Delta</math>E = 12,09eV - 10,2eV in Form eines Photons ab, das wir als Licht wahrnehmen. Nach einer kurzen Zeit geht es weiter in seinen Grundzustand m = 1 und gibt dabei die Energiedifferenz dieser beiden Bahnen <math>\Delta</math>E=10,2eV - 0eV wieder als Photon ab. Allerdings sehen wir dieses Photon nicht, da es im UV-Bereich ist. <br> | ||
Das Elektron hätte aber auch von der Bahn m = 3 gleich auf die Bahn m = 1 springen können. Dabei hätte es dann die Energie <math>\Delta</math>E = 12,09eV - 0eV abgegeben. Das Atom sendet dann das Photon mit der Energie E = 12,09eV aus, welches wir wieder nicht sehen, da es im UV-Bereich ist.<br> | Das Elektron hätte aber auch von der Bahn m = 3 gleich auf die Bahn m = 1 springen können. Dabei hätte es dann die Energie <math>\Delta</math>E = 12,09eV - 0eV abgegeben. Das Atom sendet dann das Photon mit der Energie E = 12,09eV aus, welches wir wieder nicht sehen, da es im UV-Bereich ist.<br> | ||
| + | In Bohrschen Atommodell kann man die Entstehung der Photonen mit diesem Bild erklären:<br> | ||
| + | <center>[[File:Hydrogen_transitions.svg|400px]]</center> | ||
| + | |||
{{Merke|1=Ist das Elektron auf der innersten Bahn m = 1, dann ist das Wasserstoffatom bzw. das Elektron im Grundzustand. Wird das Elektron in der Hülle des Wasserstoffatoms auf eine Bahn m > 1 gehoben, dann ist das Wasserstoffatom angeregt und das Elektron hat nun auf der Bahn m eine höhere Energie, die genau der Energiedifferenz der Bahnen m und 1 entspricht. <br> | {{Merke|1=Ist das Elektron auf der innersten Bahn m = 1, dann ist das Wasserstoffatom bzw. das Elektron im Grundzustand. Wird das Elektron in der Hülle des Wasserstoffatoms auf eine Bahn m > 1 gehoben, dann ist das Wasserstoffatom angeregt und das Elektron hat nun auf der Bahn m eine höhere Energie, die genau der Energiedifferenz der Bahnen m und 1 entspricht. <br> | ||
Der Übergang des angeregten Atoms in den Grundzustand kann auf verschiedene Arten erfolgen. Das Elektron kann gleich auf seine Bahn m = 1 gehen und das Atom gibt dabei die Energiedifferenz der zwei Energieniveaus der Bahnen als Photon ab. Oder das Elektron geht über eine oder mehrere innere Bahnen in den Grundzustand. Dabei werden jeweils die Energiedifferenzen der Energieniveaus der Bahnen als Photonen abgegeben. Nur bei Übergängen auf die Bahn m = 2 sehen wir die ausgesendeten Photonen als Licht. | Der Übergang des angeregten Atoms in den Grundzustand kann auf verschiedene Arten erfolgen. Das Elektron kann gleich auf seine Bahn m = 1 gehen und das Atom gibt dabei die Energiedifferenz der zwei Energieniveaus der Bahnen als Photon ab. Oder das Elektron geht über eine oder mehrere innere Bahnen in den Grundzustand. Dabei werden jeweils die Energiedifferenzen der Energieniveaus der Bahnen als Photonen abgegeben. Nur bei Übergängen auf die Bahn m = 2 sehen wir die ausgesendeten Photonen als Licht. | ||
Version vom 5. Mai 2021, 07:50 Uhr
Ein Regenbogen entsteht, wenn Sonnenlicht auf Regentropfen beim Abregnen einer Wolke unter einem bestimmten Winkel treffen.
Mit einem Prisma kann man die Farbzerlegung weißen Lichtes zeigen.
Man sieht wie bei einem Durchgang durch Glas das weiße Licht in seine Spektralfarben aufgespalten wird.
| Im folgenden Video wird es erklärt | Wem im linken Video zu viel Englisch gesprochen wurde, kann sich dieses Video auf Deutsch ansehen: |
| |
|
 Merke:
Durch Brechung in einem Medium wie Glas wird weißes Licht in seine Spektralfarben aufgespaltet. Weißes Licht besteht aus allen Farben unseres Farbspektrums. |
Es gibt aber nicht nur die Sonne oder Glühlampen die Licht aussenden und wir dieses Licht als weiß sehen. Manche Glühlampen haben einen gelben oder bläulichen Farbton. Wenn man in Chemie Natrium verbrennt, dann sieht man gelbes Licht.
 Versuch
Schau dir dieses Videos an und notiere deine Beobachtungen. |
| Merke:
Die Spektren leuchtender Körper können einen kontinuierlichen Verlauf haben (Sonnenlicht, Glühlampe). Sie haben ein kontinuierliches Spektrum. Dieses sieht man, wenn das Licht durch ein Prisma geht, dabei gebrochen wird und in seine Spektralfarben zerlegt wird. |
| Versuch
Im nächsten Video geht es um das Sichtbarmachen von Linienspektren. Im Unterricht hätten wir das ausgesendete Licht hinter einem Prisma beobachtet. In dem Video werden Gitter verwendet, die auch weißes Licht aufspalten. Schau dir hierzu die ersten 10 Minuten des Videos an. Auf dieser Seite von Leifiphysik wird das Zustandekommen von Spektren mit schönen Applets erklärt. |
| Spektrum einer | ||
| Quecksilberdampflampe | Natriumdampflmape | Wasserstoff |
 |
 |
|
| Merke:
In der Atomhülle sind die Elektronen auf bestimmten Bahnen um den Kern. Auf diesen Bahnen haben die Elektronen ganz bestimmte Energiewerte. Zwischenwerte für Elektronen gibt es in der Atomhülle nicht. Das Atom hat diskrete Energieniveaus.  Das Atom ist dann in einem angeregten Zustand. |
Für das Wasserstoffatom kann man die Situation so darstellen. Das Wasserstoffatom besteht aus einem Proton im Atomkern und einem Hüllenelektron. Dieses Hüllenelektron kann sich auf verschiedenen Bahnen um den Atomkern bewegen. Normalerweise ist es auf der innersten Bahn.
Die waagrechten Linien sind die Energieniveaus der Bahnen von Elektronen. Auf der innersten Bahn ist das Elektron bei m = 1 (links unten im Diagramm.) Führt man dem Elektron nun Energie zu, dass es auf eine höhere Bahn gelangt, indem man ihm genau die Energiedifferenz der Bahnen zufügt, dann wird das Elektron auf eine höhere Bahn gehoben und hat nun diese Energiedifferenz mehr Energie. Zum Beispiel kann es auf die Bahn m = 3 gehoben werden. Es hat nun 12,09eV mehr Energie als auf seiner innersten Bahn. 1eV (Elektronenvolt) ist eine Energieeinheit, die im atomaren Bereich verwendet wird. Es ist 1eV = 1,6·10-19J.
Das Elektron bleibt aber nicht auf der Bahn m = 3. Es will wieder auf eine Bahn niedrigerer Energie wechseln. Von der Bahn m = 3 kann es auf die Bahn mit m = 2 heruntergehen. Dabei gibt es die Energie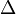 
E = 12,09eV - 10,2eV in Form eines Photons ab, das wir als Licht wahrnehmen. Nach einer kurzen Zeit geht es weiter in seinen Grundzustand m = 1 und gibt dabei die Energiedifferenz dieser beiden Bahnen 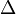E=10,2eV - 0eV wieder als Photon ab. Allerdings sehen wir dieses Photon nicht, da es im UV-Bereich ist.
Das Elektron hätte aber auch von der Bahn m = 3 gleich auf die Bahn m = 1 springen können. Dabei hätte es dann die Energie 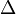E = 12,09eV - 0eV abgegeben. Das Atom sendet dann das Photon mit der Energie E = 12,09eV aus, welches wir wieder nicht sehen, da es im UV-Bereich ist.
In Bohrschen Atommodell kann man die Entstehung der Photonen mit diesem Bild erklären:
 Merke
Ist das Elektron auf der innersten Bahn m = 1, dann ist das Wasserstoffatom bzw. das Elektron im Grundzustand. Wird das Elektron in der Hülle des Wasserstoffatoms auf eine Bahn m > 1 gehoben, dann ist das Wasserstoffatom angeregt und das Elektron hat nun auf der Bahn m eine höhere Energie, die genau der Energiedifferenz der Bahnen m und 1 entspricht. Rotes Licht ist energieärmer als blaues Licht, also entsteht die orange (rote) Linie beim Übergang von m = 3 zu m = 2, die türkise (hellblaue) Linie beim Übergang von m = 4 zu m = 2, die nächste blaue Linie beim Übergang von m = 5 zu m = 2, ... |
| Merke:
Die Energie eines Photons ist abhängig von seiner Frequenz (Farbe des Lichts). Sie ist am größten am blauen Rand des Spektrums und am kleinsten am roten Rand des Spektrums.  Die Energie eines Photons ist durch E = h·f gegeben. Dabei ist f die Frequenz des Photons und h = 6,626·10-34Js das Plancksche Wirkungsquantum. |
