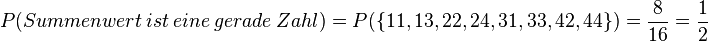M9 Mehrstufige Zufallsexperimente: Unterschied zwischen den Versionen
Aus RSG-Wiki
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 55: | Zeile 55: | ||
| − | {{Aufgaben-blau|2|2=Buch S. 146 / | + | {{Aufgaben-blau|2|2=Buch S. 146 / 3<br> |
Buch S. 146 / 4<br> | Buch S. 146 / 4<br> | ||
| − | Buch S. 146 / 5 [[Datei:Wuerfel_w4.jpg|100px]] | + | Buch S. 146 / 5 [[Datei:Wuerfel_w4.jpg|100px]] <br> |
Buch S. 146 / 6 }} | Buch S. 146 / 6 }} | ||
| Zeile 74: | Zeile 74: | ||
b) <math>P(E_2)=P(\lbrace 11, 22, 33, 44, 55, 66 \rbrace)= \frac{1}{6}\cdot \frac{1}{6} +\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}=6\cdot \frac{1}{36}= \frac{1}{6}\approx 16,7%</math> | b) <math>P(E_2)=P(\lbrace 11, 22, 33, 44, 55, 66 \rbrace)= \frac{1}{6}\cdot \frac{1}{6} +\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}=6\cdot \frac{1}{36}= \frac{1}{6}\approx 16,7%</math> | ||
| − | c)<math>E_3=\overline { | + | c)<math>E_3=\overline {E_2} \Rightarrow P(E_3)=1-P(E_2)=1-\frac{1}{6}=\frac{5}{6}\approx 83,3%</math> |
d) <math>P(E_4)=P(\lbrace 46, 55, 64\rbrace)=\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}=\frac{1}{12}\approx 8,3%</math> | d) <math>P(E_4)=P(\lbrace 46, 55, 64\rbrace)=\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}+\frac{1}{6}\cdot \frac{1}{6}=\frac{1}{12}\approx 8,3%</math> | ||
| Zeile 89: | Zeile 89: | ||
| − | 146/ | + | 146/4<br> |
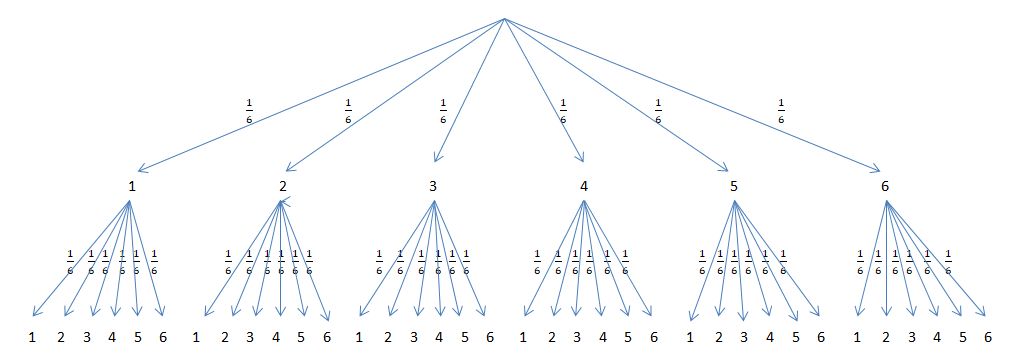
Zu diesem Zufallsexperiment lässt sich nur sehr schwer ein Baumdiagramm zeichnen. Daher ist es das einfachste, wenn man das Baumdiagramm aus der vorhergehenden Aufgabe sich im Kopf weiter fortgesetzt vorstellt. An jedem Ast steht die Wahrscheinlichkeit <math>\frac{1}{6}</math>. | Zu diesem Zufallsexperiment lässt sich nur sehr schwer ein Baumdiagramm zeichnen. Daher ist es das einfachste, wenn man das Baumdiagramm aus der vorhergehenden Aufgabe sich im Kopf weiter fortgesetzt vorstellt. An jedem Ast steht die Wahrscheinlichkeit <math>\frac{1}{6}</math>. | ||
| Zeile 101: | Zeile 101: | ||
c) <math>P(E_3)=P(\lbrace 6666, 1111 \rbrace)= \left (\frac{1}{6}\right )^4 + \left (\frac{1}{6}\right )^4=2\cdot \left (\frac{1}{6}\right )^4</math> | c) <math>P(E_3)=P(\lbrace 6666, 1111 \rbrace)= \left (\frac{1}{6}\right )^4 + \left (\frac{1}{6}\right )^4=2\cdot \left (\frac{1}{6}\right )^4</math> | ||
| − | d) <math>P(E_4)=\left (\frac{5}{6}\right )^4 </math> | + | d) Wenn die Zahl die Ziffer 1 nicht enthält steht an jeder Stelle eine der Zahlen 2, 3, 4, 5, 6. Also hat man für jede Ziffer 5 Möglichkeiten. Im Baumdiagramm kann man sich vorstellen: eine Verzweigung nach links zur 1 mit Wahrscheinlichkeit <math>\frac{1}{6}</math>, eine zweite Verzweigung nach rechts zu 2, 3, 4, 5, 6 mit der Wahrscheinlichkeit <math>\frac{5}{6}</math>. Und man geht bei den 4 Verzweigungen jeweils den rechten Weg. <br> |
| + | <math>P(E_4)=\left (\frac{5}{6}\right )^4 </math> | ||
| − | e) <math>P(E_5)=4\cdot \frac{1}{6}\cdot \left (\frac{1}{6}\right )^3</math> | + | e) Im Baumdiagramm kann man sich vorstellen: eine Verzweigung nach links zur 6 mit Wahrscheinlichkeit <math>\frac{1}{6}</math>, eine zweite Verzweigung nach rechts zu 1, 2, 3, 4, 5 mit der Wahrscheinlichkeit <math>\frac{5}{6}</math>. Und man geht einmal nach links und dreimal den rechten Weg. Dabei hat man 4 Möglichkeiten einmal nach links zu gehen. <br> |
| + | Also ist <math>P(E_5)= P(\lbrace 6xyz, x6yz, xy6z, xyz6 \rbrace)=\frac{1}{6}\cdot \frac{5}{6}\cdot \frac{5}{6}\cdot \frac{5}{6} + \frac{5}{6}\cdot \frac{1}{6} \cdot \frac{5}{6}\cdot \frac{5}{6} + \frac{5}{6}\cdot \frac{5}{6}\cdot \frac{1}{6} \cdot \frac{5}{6} + \frac{5}{6}\cdot \frac{5}{6}\cdot \frac{5}{6} \cdot \frac{1}{6}=4\cdot \frac{1}{6}\cdot \left (\frac{1}{6}\right )^3</math> | ||
| − | f) <math>P(E_6)=1-P(''Die\ Zahl\ enthaelt\ keine\ 6'')=1- \left (\frac{5}{6}\right )^4</math> | + | f) Hier nimmt man die Berechnung über das Gegenereignis.<br> |
| + | <math>P(E_6)=1-P(''Die\ Zahl\ enthaelt\ keine\ 6'')=1- \left (\frac{5}{6}\right )^4</math> | ||
| − | g) <math>P(E_7)=4\cdot \frac{1}{6}\cdot \left (\frac{1}{6}\right )^ | + | g) Dieses Ereignis setzt sich zusammen aus den zwei Ereignissen E<sub>4</sub>, die Ziffer 1 kommt überhaupt nicht vor und dem Ereignis E<sub>5</sub>, nur mit Ziffer 1 statt 6.<br> |
| + | <math>P(E_7)=4\cdot \frac{1}{6}\cdot \left (\frac{1}{6}\right )^3+ \left (\frac{5}{6}\right )^4</math> | ||
| − | h) <math>P(E_8)= \left (\frac{ | + | h) Wenn die 1 nur an der vierten Stelle vorkommen darf, dann hat man im Baumdiagramm wieder jeweils 2 Verzweigungen, eine nach links zu 1 mit der Wahrscheinlichkeit <math>\frac{1}{6}</math> und eine nach rechts zu 2, 3, 4, 5, 6 mit der Wahrscheinlichkeit <math>\frac{5}{6}</math>. Die ersten dreimal geht man nach rechts und beim vierten Mal nach links.<br> |
| + | <math>P(E_8)= \left (\frac{5}{6}\right )^3 \cdot \left (\frac{1}{6}\right )=\frac{5^3}{6^4} </math> | ||
| Zeile 122: | Zeile 127: | ||
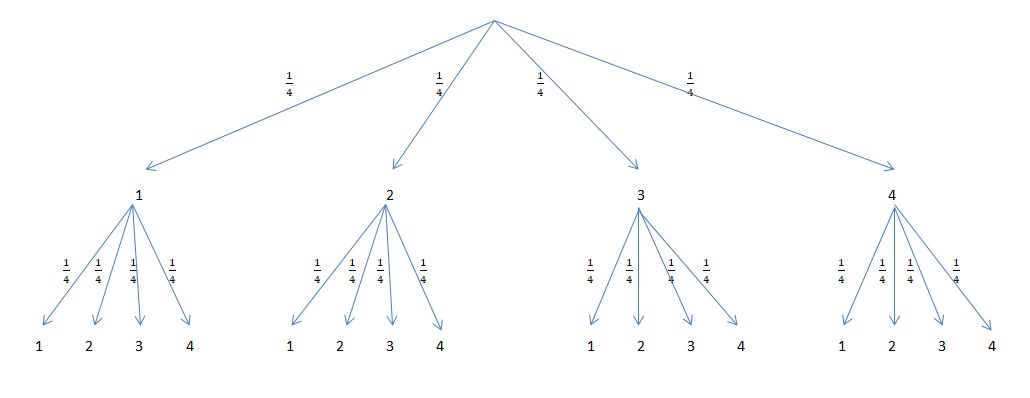
Man sieht, dass es 16 Ergebnisse gibt. <math>\omega=\lbrace 11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44 \rbrace </math>. Für jeden Ast ist die Wahrscheinlichkeit <math>\frac{1}{4}</math>. | Man sieht, dass es 16 Ergebnisse gibt. <math>\omega=\lbrace 11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44 \rbrace </math>. Für jeden Ast ist die Wahrscheinlichkeit <math>\frac{1}{4}</math>. | ||
| − | <math>P(Summenwert ist eine gerade Zahl)=P(\lbrace 11, 13, 22, 24, 31, 33, 42, 44 \rbrace)=\frac{8}{16}=\frac{1}{2}</math> | + | <math>P(Summenwert\ ist\ eine\ gerade\ Zahl)=P(\lbrace 11, 13, 22, 24, 31, 33, 42, 44 \rbrace)=\frac{8}{16}=\frac{1}{2}</math> |
| + | |||
| + | b) Du kannst gerne einen Tetraeder-Würfel basteln oder du hast vielleicht sogar eine solchen Würfel daheim. Dann überprüfe doch mal Aufgabe a). | ||
| − | |||
146/6<br> | 146/6<br> | ||
Aktuelle Version vom 6. Mai 2021, 12:14 Uhr
In diesem Video
werden alle Begriffe und die Pfadregeln nochmals an der Tafel erkärt.
|
|
In diesem Video siehst du wie man mit dem Gegenereignis und den Pfadregeln eine Wahrscheinlichkeit beim Elfmeterschießen berechnet.


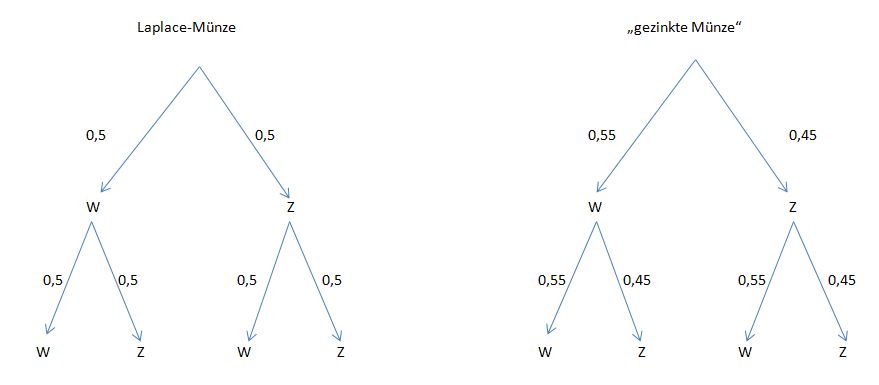
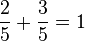 . Rechts ist nach dem zweiten unteren Verzweigungspunkt
. Rechts ist nach dem zweiten unteren Verzweigungspunkt 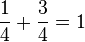 und nach dem zweiten oberen Verzweigungspunkt
und nach dem zweiten oberen Verzweigungspunkt 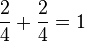 .
.
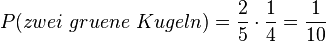 ,
,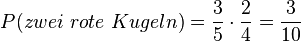 ,
, 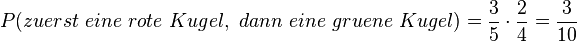 ,
, 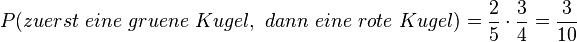
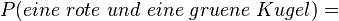
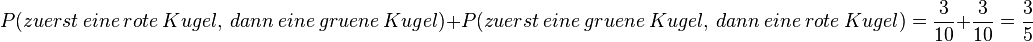
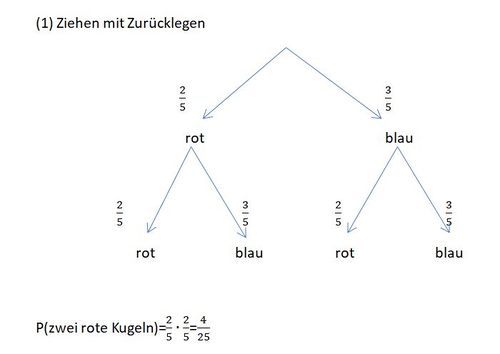
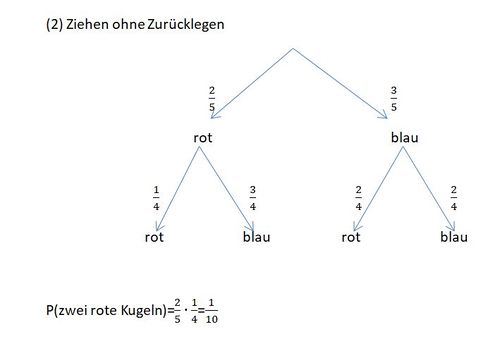
 ist das Gegenereignis des Ereignisses
ist das Gegenereignis des Ereignisses  . Für die Wahrscheinlichkeit
. Für die Wahrscheinlichkeit  gilt:
gilt: 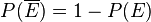 .
.

 .
.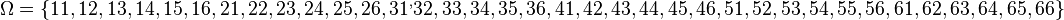 .
.
 kennt, kann man mit der Laplace-Wahrscheinlichkeit
kennt, kann man mit der Laplace-Wahrscheinlichkeit 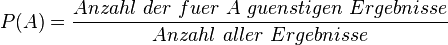 die Wahrscheinlichkeit berechnen.
die Wahrscheinlichkeit berechnen.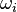 die Wahrscheinlichkeit
die Wahrscheinlichkeit 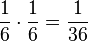 hat.
Alle Elementarereignisse
hat.
Alle Elementarereignisse 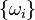 sind also gleichwahrscheinlich mit
sind also gleichwahrscheinlich mit 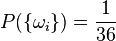 .
.
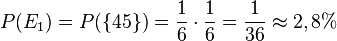
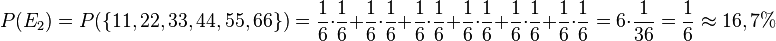
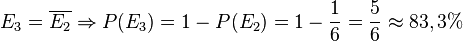
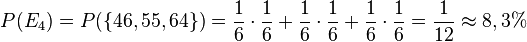
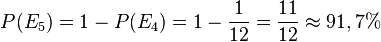
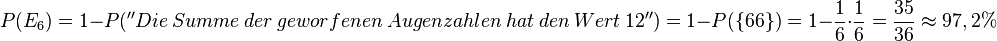
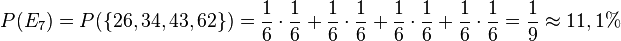
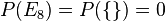
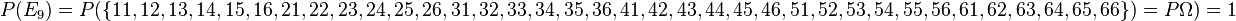
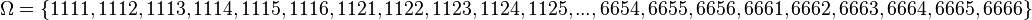 und
und 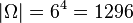 .
.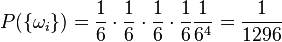 .
.
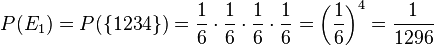
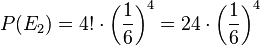
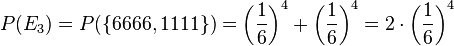
 . Und man geht bei den 4 Verzweigungen jeweils den rechten Weg.
. Und man geht bei den 4 Verzweigungen jeweils den rechten Weg. 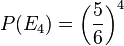
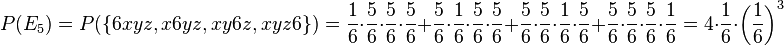

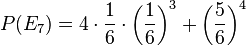
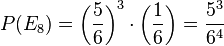

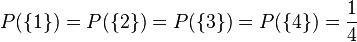 .
.
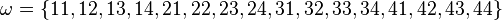 . Für jeden Ast ist die Wahrscheinlichkeit
. Für jeden Ast ist die Wahrscheinlichkeit  .
.