M11 Stochastische Unabhängigkeit: Unterschied zwischen den Versionen
| Zeile 44: | Zeile 44: | ||
{{Merke|1=Man prüft ob zwei Ereignisse A und B stochastisch unabhängig sind, indem man schaut, ob die Gleichung <math>P(A \cap B)=P(A)\cdot P(B)</math> gültig ist. }} | {{Merke|1=Man prüft ob zwei Ereignisse A und B stochastisch unabhängig sind, indem man schaut, ob die Gleichung <math>P(A \cap B)=P(A)\cdot P(B)</math> gültig ist. }} | ||
| − | {{Aufgaben-blau| | + | {{Aufgaben-blau|3|2=Bearbeite auf der [https://de.serlo.org/mathe/25630/aufgaben-zum-thema-unabh%C3%A4ngigkeit-von-ereignissen Seite] die Aufgaben 1 und 2.}} |
{{Merke|1=Sind zwei Ereignisse A und B stochastisch unabhängig, dann ist <math>P(A \cap B)=P(A)\cdot P(B)</math>. }} | {{Merke|1=Sind zwei Ereignisse A und B stochastisch unabhängig, dann ist <math>P(A \cap B)=P(A)\cdot P(B)</math>. }} | ||
| − | {{Aufgaben-blau| | + | {{Aufgaben-blau|4|2=Bearbeite die Aufgaben auf [https://matheportal.files.wordpress.com/2016/07/lc3b6sungen-zu-den-c3bcbungen-zur-stochastischen-unabhc3a4ngigkeit1.pdf dieser Seite]. ''Nicht gleich die Lösungen anschauen!'' }} |
Version vom 8. Mai 2021, 09:20 Uhr
Wann sind zwei Eigenschaften unabhängig oder abhängig voneinander? Bei den Vierfeldertafeln hat man immer zwei Eigenschaften und trägt die (absoluten oder relativen) Häufigkeiten oder Wahrscheinlichkeiten dazu ein.
Was heißt nun in der Stochastik, dass die zwei Eigenschaften stochastisch unabhängig oder stochastisch abhängig sind.
Man betrachtet die zwei Eigenschaften "blond" und "weiblich" und stellt sich den Extremfall vor, dass jede weibliche Person blond ist. Jede weibliche Person ist blond und jede nicht blonde Person ist dann nicht weiblich. Hier wird man sicher sagen, dass die beiden Eigenschaften "blond" und "weiblich" voneinander abhängig sind. Welche Bedingungen müssen gegeben sein, dass die zwei Eigensschaften unabhängig sind?
|
Merke:
Zwei Ereignisse A und B heißen stochastisch unabhängig, wenn das Eintreten des einen Ereignisses nicht die Wahrscheinlichkeit für das Eintreten des anderen Ereignisses ändert. |
In unserem Fall der zwei Eigenschaften "blond" und "weiblich" würde das bedeuten, dass der Anteil von "blond" unter den weiblichen Personen genauso groß ist wie unter den nicht weiblichen Personen bzw in der gesamten Bevölkerung. Das Eintreten von "weiblich" oder "nicht-weiblich" soll die Eigenschaft "blond" nicht beeinflussen und umgekehrt. Das ist der Fall, wenn "weiblich" unter den blonden Personen genauso vertreten ist, wie in der Grundgesamtheit, wenn also ihr Anteil in beiden Fällen gleich ist.
Die Ereignisse sind unabhängig, wenn
a) die Eigenschaft "blond" zu sein ist unter männlichen wie weiblichen Personen gleich ist.
In dem folgenden Video wird stochastisch unabhängig oder stochastisch abhängig jeweils an den zwei Beispiel erklärt und gelöst.
|
Zwei Ereignisse sind stochastisch unabhängig, wenn |
Wiederholung: Die bedingte Wahrscheinlichkeit 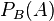 erhält man mit der Formel
erhält man mit der Formel 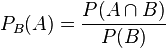
Ist nun 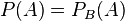 , dann gilt für die Formel der bedingten Wahrscheinlichkeit
, dann gilt für die Formel der bedingten Wahrscheinlichkeit 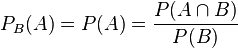 und wenn man umformt:
und wenn man umformt: 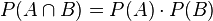
|
Merke:
Zwei Ereignisse A und B sind stochastisch unabhängig, wenn Ist |
In diesen Videos wird untersucht, ob die beiden Ereignisse stochastich unabhängig oder abhängig sind:
|
Man prüft ob zwei Ereignisse A und B stochastisch unabhängig sind, indem man schaut, ob die Gleichung |
|
Sind zwei Ereignisse A und B stochastisch unabhängig, dann ist |

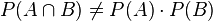 , dann heißen die beiden Ereignisse A und B stochastisch abhängig.
, dann heißen die beiden Ereignisse A und B stochastisch abhängig.

