M9 Quadratische Funktionen und lineare Gleichungssysteme: Unterschied zwischen den Versionen
| (23 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
Er beschreibt die besonderheit des [https://structurae.net/de/bauwerke/gateway-arch Gateway Arch], dass die Breite unten am Fuß genauso groß ist wie die Höhe des Bauwerks, nämlich 192m. Und es erinnert ihn sehr an eine Parabel. | Er beschreibt die besonderheit des [https://structurae.net/de/bauwerke/gateway-arch Gateway Arch], dass die Breite unten am Fuß genauso groß ist wie die Höhe des Bauwerks, nämlich 192m. Und es erinnert ihn sehr an eine Parabel. | ||
| − | Kannst du eine Parabelgleichung für den Bogen angeben? | + | {{Aufgaben-blau|1|2=Kannst du eine Parabelgleichung für den Bogen angeben?}} |
{{Lösung versteckt|1=Legt man in den linken unteren Fußpunkt den Ursprung eines Koordinatensystems, so ist der rechte Fußpunkt bei (192;0) und der Scheitel S(96;192).<br> | {{Lösung versteckt|1=Legt man in den linken unteren Fußpunkt den Ursprung eines Koordinatensystems, so ist der rechte Fußpunkt bei (192;0) und der Scheitel S(96;192).<br> | ||
| Zeile 15: | Zeile 15: | ||
Also erhält man als Parabelgleichung <math>y=-\frac{1}{48}(x-96)^2+192</math><br> | Also erhält man als Parabelgleichung <math>y=-\frac{1}{48}(x-96)^2+192</math><br> | ||
Man bringt diese Gleichung noch auf die normale Form <math>-\frac{1}{48}(x^2-192x+ 96^2)+192=-\frac{1}{48}x^2+4x -192+192=-\frac{1}{48}x^2 + 4x</math>, also <math>y=-\frac{1}{48}x^2 + 4x</math>. }} | Man bringt diese Gleichung noch auf die normale Form <math>-\frac{1}{48}(x^2-192x+ 96^2)+192=-\frac{1}{48}x^2+4x -192+192=-\frac{1}{48}x^2 + 4x</math>, also <math>y=-\frac{1}{48}x^2 + 4x</math>. }} | ||
| + | |||
Wenn der Scheitel S und eine Nullstelle gegeben ist kann man mit der Scheitelform relativ leicht eine Parabelgleichung angeben. | Wenn der Scheitel S und eine Nullstelle gegeben ist kann man mit der Scheitelform relativ leicht eine Parabelgleichung angeben. | ||
| Zeile 50: | Zeile 51: | ||
Nun fassst man die beiden Gleichungen zusammen<br> | Nun fassst man die beiden Gleichungen zusammen<br> | ||
B: <math>16 = 16a + 4b</math><br> | B: <math>16 = 16a + 4b</math><br> | ||
| − | C: <math>6 = a-b</math> | + | C: <math>6 = a-b</math><br> |
Nun kann man die Gleichung von B durch 4 teilen und nach b auf lösen und hat dann <math>b=4-4a</math>. Setzt man dies in die Gleichung für C ein, dann hat man <math>6=a-(4-4a)</math>. Da vor b ein - steht, macht man um 4-4a Klammern!<br> | Nun kann man die Gleichung von B durch 4 teilen und nach b auf lösen und hat dann <math>b=4-4a</math>. Setzt man dies in die Gleichung für C ein, dann hat man <math>6=a-(4-4a)</math>. Da vor b ein - steht, macht man um 4-4a Klammern!<br> | ||
<math>6=a-4+4a</math> --> <math>10 = 5a</math> --> <math>a = 2</math><br> | <math>6=a-4+4a</math> --> <math>10 = 5a</math> --> <math>a = 2</math><br> | ||
Damit ist dann <math>b= 4-4a = 4-4\cdot 2=-4</math><br> | Damit ist dann <math>b= 4-4a = 4-4\cdot 2=-4</math><br> | ||
| − | Die Funktionsgleichung bzw. die Gleichung der Parabel ist <math>y= | + | Die Funktionsgleichung bzw. die Gleichung der Parabel ist <math>y=2x^2-4x+2</math> |
'''3. Beispiel''': Gegeben sind die zwei Punkte P(0;0), S(0,5;1,5), wobei S der Scheitelpunkt ist. <br> | '''3. Beispiel''': Gegeben sind die zwei Punkte P(0;0), S(0,5;1,5), wobei S der Scheitelpunkt ist. <br> | ||
| − | Hier sind nur zwei | + | Hier sind nur zwei Punkte gegeben, aber der Scheitel ist dabei. Damit könnten wir es mit der Scheitelform machen.<br> |
<math>y=a(x-0,5)^2-1,5</math> und <math>0=a(1-0,5)^2+1,5</math>. <br> | <math>y=a(x-0,5)^2-1,5</math> und <math>0=a(1-0,5)^2+1,5</math>. <br> | ||
Die zweite Gleichung liefert <math>0 =a\cdot 0,25+1,5</math> und <math>a=-6</math>.<br> | Die zweite Gleichung liefert <math>0 =a\cdot 0,25+1,5</math> und <math>a=-6</math>.<br> | ||
Also ist die Parabelgleichung <math>y = -6(x-0,5)^2+1,6</math> oder <math>y=-6x^2+6x</math> | Also ist die Parabelgleichung <math>y = -6(x-0,5)^2+1,6</math> oder <math>y=-6x^2+6x</math> | ||
| − | Es geht aber auch mit der Methode, die wir gerade kennengelernt haben. Der allgemeine Ansatz ist wieder <math> | + | Es geht aber auch mit der Methode, die wir gerade kennengelernt haben. Der allgemeine Ansatz ist wieder <math>y=ax^2+bx+c</math><br> |
Punkt P(0;0) --> <math>0=a\cdot 0^2+b\cdot 0 + c</math><br> | Punkt P(0;0) --> <math>0=a\cdot 0^2+b\cdot 0 + c</math><br> | ||
Punkt S(0,5;1,5) --> <math>1,5=a\cdot 0,5^2 + b\cdot 0,5 +c</math><br> | Punkt S(0,5;1,5) --> <math>1,5=a\cdot 0,5^2 + b\cdot 0,5 +c</math><br> | ||
Aus der Gleichung für P erhält man <math>c=0</math>. Dies setzt man in die Gleichung von S ein.<br> | Aus der Gleichung für P erhält man <math>c=0</math>. Dies setzt man in die Gleichung von S ein.<br> | ||
| − | <math>1,5=0,25a+0,5b</math>. | + | <math>1,5=0,25a+0,5b</math>.<br> |
| − | Nun hat man aber eine Gleichung aber mit zwei Unbekannten. Wie soll man das lösen? Dafür | + | Nun hat man aber eine Gleichung aber mit zwei Unbekannten. Wie soll man das lösen? Dafür gibt es unendlich viele Lösungen.<br> |
Nun erinnert man sich, dass diese Parabel noch eine zweite Nullstelle hat. Die x-Koordinate von S liegt in der Mitte der beiden Nullstellen, also ist die zweite Nullstelle Q(1;0) und damit hat man eine dritte Gleichung.<br> | Nun erinnert man sich, dass diese Parabel noch eine zweite Nullstelle hat. Die x-Koordinate von S liegt in der Mitte der beiden Nullstellen, also ist die zweite Nullstelle Q(1;0) und damit hat man eine dritte Gleichung.<br> | ||
Punkt Q --> <math>0=a\cdot 1^2+b\cdot 1</math>.<br> | Punkt Q --> <math>0=a\cdot 1^2+b\cdot 1</math>.<br> | ||
| Zeile 74: | Zeile 75: | ||
Q --> <math>0 = a+b</math><br> | Q --> <math>0 = a+b</math><br> | ||
Man löst die Glelichung für Q nach a auf --> <math> a = -b</math> und setzt dies in die Gleichung für P ein.<br> | Man löst die Glelichung für Q nach a auf --> <math> a = -b</math> und setzt dies in die Gleichung für P ein.<br> | ||
| − | <math>1,5 = 0,25\cdot (-b) + 0,5b</math> --> <math>1,5=0,25b</math> und b<math>b=6</math>. | + | <math>1,5 = 0,25\cdot (-b) + 0,5b</math> --> <math>1,5=0,25b</math> und b<math>b=6</math>.<br> |
Damit ist <math>a=-6</math> und die Gleichung der Parabel <math>y=-6x^2+6x</math>, also das selbe Ergebnis wie oben. | Damit ist <math>a=-6</math> und die Gleichung der Parabel <math>y=-6x^2+6x</math>, also das selbe Ergebnis wie oben. | ||
| Zeile 80: | Zeile 81: | ||
Hier stellt man wieder zum allgemeinen Ansatz <math>y = a^2+bx+c</math> drei Gleichungen auf.<br> | Hier stellt man wieder zum allgemeinen Ansatz <math>y = a^2+bx+c</math> drei Gleichungen auf.<br> | ||
A --> <math>7 = a\cdot (-1)^2 + b\cdot (-1) +c</math><br> | A --> <math>7 = a\cdot (-1)^2 + b\cdot (-1) +c</math><br> | ||
| − | B --> <math>1 = a\cdot 2^2 + b \ | + | B --> <math>1 = a\cdot 2^2 + b \cdot 2 +c</math><br> |
| − | c --> <math>17 = a \cdot 4^2 + b\ | + | c --> <math>17 = a \cdot 4^2 + b\cdot 4 + c</math><br> |
Wenn man etwas geübter ist kann man auch gleich die Quadrate ausrechnen und in der üblichen Schreibeweise, dass die Zahlen vor den Unbekannten stehen hinschreiben.<br> | Wenn man etwas geübter ist kann man auch gleich die Quadrate ausrechnen und in der üblichen Schreibeweise, dass die Zahlen vor den Unbekannten stehen hinschreiben.<br> | ||
A --> <math>7 = a - b +c</math><br> | A --> <math>7 = a - b +c</math><br> | ||
| Zeile 111: | Zeile 112: | ||
Wenn du dir die 4 Beispiele oben anschaust, dann siehst du, dass wir jeweils nach diesem Verfahren vorgegangen sind. Bei den ersten drei Beispielen hat man den Wert für c gleich erhalten und man hat sich den 3. Punkt des Merksatzes gespart. Im 4. Beispiel kam man so zur Lösung. | Wenn du dir die 4 Beispiele oben anschaust, dann siehst du, dass wir jeweils nach diesem Verfahren vorgegangen sind. Bei den ersten drei Beispielen hat man den Wert für c gleich erhalten und man hat sich den 3. Punkt des Merksatzes gespart. Im 4. Beispiel kam man so zur Lösung. | ||
| + | |||
| + | '''Lustig:''' Etwas einfacher geht es [https://www.pinterest.de/pin/775322892077017521/ hier] zu. Das lässt sich im Kopf lösen. | ||
| + | |||
| + | In der 8. Klasse hatten wir Gleichungssysteme etwas anders notiert. <br> | ||
| + | (1) x + y = 1<br> | ||
| + | (2) x + 2y = 2<br> | ||
| + | hat die Lösungen x = 0 und y = 1. Die Gleichungen wurden durchnummeriert. | ||
| + | |||
| + | Das macht man jetzt auch.<br> | ||
| + | (1) 6x + y - 3z = 9<br> | ||
| + | (2) 2x + 2y - z = 3<br> | ||
| + | (3) 5x - 4y - 4z = 0<br> | ||
| + | Zur Lösung löst man z.B. die Gleichung (2) nach z auf: z = 2x + 2y - 3 und setzt dies für z in die anderen zwei Gleichungen ein.<br> | ||
| + | (1) 6x + y - 3(2x + 2y -3) = 9<br> | ||
| + | (3) 5x - 4y - 4(2x + 2y -3) = 0<br> | ||
| + | Nun löst man in beiden Gleichungen die Klammern auf uns vereinfacht.<br> | ||
| + | (1) -5y = 0<br> | ||
| + | (3) -3x -12y +12 = 0<br> | ||
| + | Gleichung (1) liefert y = 0. Eingesetzt in (3) ist x = 4. <br> | ||
| + | z ergibt sich dann z = 8 + 0 - 3 = 5. Also hat das Gleichungssystem die Lösungen x = 4, y = 0 und z = 5. | ||
| + | |||
| + | {{Merke|1=Welche Unbekannte du zuerst eliminierst bleibt dir überlassen. '''Tipp:''' Nimm eine Unbekannte mit Koeffizient 1. | ||
| + | |||
| + | Welches Verfahren (Einsetzverfahren, Gleichsetzverfahren, Additionsverfahren) du dann zum Lösen der zwei Gleichungen mit den verbliebenen zwei Unbekannten wählst bleibt auch dir überlassen. '''Tipp:''' Nimm das, bei dem du dich am sichersten fühlt. }} | ||
| + | |||
| + | {{Aufgaben-blau|2|2=1. Löse im Kopf: <br> | ||
| + | a) <br> | ||
| + | (1) x + 2 = 3<br> | ||
| + | (2) y = 2x<br> | ||
| + | (3) y = 5x | ||
| + | |||
| + | b)<br> | ||
| + | (1) x² = 4<br> | ||
| + | (2) y = 0,5 x²<br> | ||
| + | (3) z = x + y | ||
| + | |||
| + | c) <br> | ||
| + | (1) x = y + 2<br> | ||
| + | (2) y = 144 : 9<br> | ||
| + | (3) z = x + 3y | ||
| + | |||
| + | d) <br> | ||
| + | (1) x + y = 5<br> | ||
| + | (2) y = z<br> | ||
| + | (3) y + z = 8 | ||
| + | |||
| + | e) <br> | ||
| + | (1) x = 5<br> | ||
| + | (2) y = 7 - 2x<br> | ||
| + | (3) z = (x+y):2 | ||
| + | |||
| + | f)<br> | ||
| + | (1) x = 2y + 3z<br> | ||
| + | (2) y = 0,75z<br> | ||
| + | (3) z + 12 = -2z | ||
| + | |||
| + | 2. Ermittle jeweils die Lösungsmenge (Grundmenge ist die Menge der reellen Zahlen<br> | ||
| + | a) <br> | ||
| + | (1) 6x + y - 3z = 9<br> | ||
| + | (2) 2x + 2y - z = 3<br> | ||
| + | (3) 5x - 4y - 4z = 0 | ||
| + | |||
| + | b) <br> | ||
| + | (1) x + y + z = 12<br> | ||
| + | (2) x - y + z = 4<br> | ||
| + | (3) x - y -z = -6 | ||
| + | |||
| + | c) <br> | ||
| + | (1) 2x - 2y + 3z = 18<br> | ||
| + | (2) 5x - y - z = 3<br> | ||
| + | (3) 12x + 4y - 2z = -4 | ||
| + | |||
| + | d) <br> | ||
| + | (1) 3x - 2y + 3z = -13<br> | ||
| + | (2) x - 3y = 13 + 4z<br> | ||
| + | (3) x - 2y + z = -3 | ||
| + | |||
| + | e) <br> | ||
| + | (1) 2x - 6y = 5 - 5x - 4z<br> | ||
| + | (2) 7x -3( x - y) = 7<br> | ||
| + | (3) 2(x + 3y) + 1 = 6y + 3z | ||
| + | |||
| + | f) <br> | ||
| + | (1) 4y - 6x = 3z - 2<br> | ||
| + | (2) 1,5(x + z) + 1 = 3y<br> | ||
| + | (3) x = 2(y - z) | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1=1a) x = 1, y = 2, z = 5<br> | ||
| + | b) x = 2, y = 2, z = 4 oder x = -2, y = 2, z = 0<br> | ||
| + | c) x = 18, y = 16, Z = 66<br> | ||
| + | d) x = 1, y = 4, z = 4<br> | ||
| + | e) x = 5, y = -3, z = 1<br> | ||
| + | f) x = -18, y = -3, z = -4 | ||
| + | |||
| + | 2a) x = 4, y = 0, z = 5 | ||
| + | |||
| + | b) x = 3, y = 4, z = 5<br> | ||
| + | Man erhält die Lösungen, indem man z.B. so vorgeht:<br> | ||
| + | Gleichung (1) nach z auflösen: z=12 - x - y und diesen Term für z in (2) und (3) einsetzen.<br> | ||
| + | (2) x - y + (12 - x - y) = 4<br> | ||
| + | (3) x - y - (12 - x - y) = -6<br> | ||
| + | Zusammenfassen:<br> | ||
| + | (2) -2y = -8<br> | ||
| + | (3) 2x = 6 <br> | ||
| + | (2) ergibt y = 4 und (3) ergibt x = 3. Für z erhält man z = 12 - 3 - 4 = 5. | ||
| + | |||
| + | c) x = 1, y = -2, z = 4<br> | ||
| + | Da (2) die einzige Gleichung ist, in der z mit Koeffizient 1 vorkommt, löst man (2) nach z auf: z = 5x - y - 3. <br> | ||
| + | Einsetzen:<br> | ||
| + | (1) 2x - 2y + 3(5x - y - 3) = 18<br> | ||
| + | (3) 12x + 4y - 2(5x - y - 3) = -4<br> | ||
| + | Zusammenfassen:<br> | ||
| + | (1) 17x - 5y = 27<br> | ||
| + | (3) 2x + 6y = - 10<br> | ||
| + | (3) nach x auflösen ergibt x = -5 - 3y. <br> | ||
| + | in (1) einsetzen:<br> | ||
| + | (1) 17(-5 - 3y) - 5y = 27<br> | ||
| + | -56y = 112 ergibt y = -2, x = 1 und z = 4. | ||
| + | |||
| + | d) x = -2, y = -1, z = -3<br> | ||
| + | e) x = 1, y = 1, z = 1<br> | ||
| + | f) <math>x=\frac{2}{3}, y = 1, z = \frac{2}{3}</math> }} | ||
| + | |||
| + | {{Aufgaben-blau|3|2=Die drei Punkte A, B und C liegen jeweils auf einer parabel. Ermittle jeweils die Funktionsgleichung der Parabel. <br> | ||
| + | a) A ( 0;2), B(4; 18), C(-1;8)<br> | ||
| + | b) A(1;3), B(-2;0), C(3;-5)<br> | ||
| + | c) A(1;0), B(2;-0,5), C(0,1)<br> | ||
| + | d) A(0,3), B(-1;0), C(2;-9) | ||
| + | |||
| + | Ändere bei jeder der Teilaufgaben die y-Koordinate des Punkts C so ab, dass durch die drei Punkte A, B und C* keine Parabel festgelegt ist. }} | ||
| + | |||
| + | {{Lösung versteckt|1=a) y = 2x<sup>2</sup> - 4x + 2 , das war das 2. Beispiel oben!<br> | ||
| + | b) a = -1, b = 0, c = 4, also y = -x<sup>2</sup> + 4<br> | ||
| + | c) <math>a=\frac{1}{4}, b = -\frac{5}{4}, c = 1</math>, also y = 0,25x<sup>2 </sup> - 1,25x + 1<br> | ||
| + | d) a = -3, b = 0, c = 3, also y = -3x<sup>2</sup> + 3 | ||
| + | |||
| + | Damit die drei Punkte auf keiner Parabel liegen, muss der Punkt C<sup>*</sup> auf der Geraden AB liegen. <br> | ||
| + | a) Die Gerade AB hat die Gleichung y = 4x + 2. Zum Beispiel liegt C<sup>*</sup>(2;10) auf der Geraden.<br> | ||
| + | b) Die Gerade AB hat die Gleichung y = x + 2. Zum Beispiel liegt C<sup>*</sup>(3;5) auf der Geraden.<br> | ||
| + | c) Die Gerade AB hat die Gleichung y = -0,5x + 0,5. Zum Beispiel liegt C<sup>*</sup>(0;0,5) auf der Geraden.<br> | ||
| + | d) Die Gerade AB hat die Gleichung y = 3x + 3. Zum Beispiel liegt C<sup>*</sup>(2;-3) auf der Geraden.<br> }} | ||
| + | |||
| + | |||
| + | '''Ausblick''': In diesem Video | ||
| + | <center>{{#ev:youtube |CrrvBqgkT84|350}}</center> | ||
| + | wird genauso wie bei uns ein Gleichungssystem mit drei Gleichungen und den Unbekannten a, b und c aufgestellt. Doch dann wird diese Gleichungssystem mit dem Additionsverfahren, so wie wir es in der 8. Klasse kennengelernt haben gelöst. Das bietet sich aber auch nur hier an, weil die Gleichungen (1) und (2) sehr, sehr ähnlich sind und man damit die Lösung für b leicht erhält. | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|4|2=1. Von den Unfallstatistiken in Städten kennt man, dass 20-jährige Fahrer 250 Unfälle in einem Jahr verursachen, 40-jährige Fahrer 150 Unfälle und 60-jährige Fahrer 200 Unfälle. <br> | ||
| + | a) Unter der Annahme, dass eine quadratische Funktion diesen Sachverhalt beschreibt, bestimme die Funktionsgleichung für die Anzahl der Unfälle als Funktion des Fahreralters.<br> | ||
| + | b) Bestimme mit dieser Funktion aus a) die Anzahl der Unfälle von 18-jährigen und 50-jährigen Fahrern.<br> | ||
| + | c) Finde mit Hilfe der Funktion aus a) in welchem Alter die Anzahl der Unfälle am geringsten ist. | ||
| + | |||
| + | 2. Bestimme jeweils die Terme quadratischer Funktionen, die die folgenden Sachverhalte beschreiben. | ||
| + | a) Tagsüber ereignen sich mit Geschwindigkeit 60 km/h 200 Unfälle, mit Geschwindigkeit 80 km/h 130 Unfälle und mit Geschwindigkeit 100 km/h 100 Unfälle.<br> | ||
| + | b) Nachts ereignen sich mit Geschwindigkeit 60 km/h 400 Unfälle, mit Geschwindigkeit 80 km/h 250 Unfälle und mit 100 km/h 250 Unfälle.<br> | ||
| + | Zeichne jeweils die Graphen der beiden Funktionen und diskutiere deine Ergebnisse. | ||
| + | }} | ||
| + | |||
| + | {{Lösung versteckt|1=1a) allgemeiner Ansatz <math>y= ax^2+bx+c</math> liefert drei Gleichungen<br> | ||
| + | (1) 250 = 400a + 20b + c<br> | ||
| + | (2) 150 = 1600a + 40b + c<br> | ||
| + | (3) 200= 3600a + 60b + c<br> | ||
| + | Löst man (1) nach c auf, so erhält man c = 250 - 400a -20b und setzt den Term für c in die Gleichungen (2) und (3), so erhält man<br> | ||
| + | (2) 150 = 1600a + 40b + 250 -400a -20b<br> | ||
| + | (3) 200 = 3600a + 60b + 250 -400a -20b<br> | ||
| + | Zusammenfassen:<br> | ||
| + | (2) -100 = 1200a + 20b<br> | ||
| + | (3) -50 = 3200a + 40b<br> | ||
| + | Mit dem Additionsverfahren 2·(2)-(3): | ||
| + | -150 = -800a liefert <math>a=\frac{150}{800}=\frac{3}{16}</math><br> | ||
| + | Setzt man <math>a=\frac{3}{16}</math> in (2), so ist <math>-100 = 1200\cdot \frac{3}{16} + 20b</math><br> | ||
| + | Zusammenfassen: -100 = 225 + 20b ergibt nach b aufgelöst <math>b=-\frac{65}{4}=-16,25</math>. <br> | ||
| + | Für c erhält man <math>c=250 - 400a -20b=250-400\cdot \frac{3}{16} - 20\cdot (-16,25)=500</math><br> | ||
| + | Also ist die Funktion <math>f:x \rightarrow \frac{3}{16} x^2 - \frac{65}{4}x+500</math>. | ||
| + | |||
| + | b) f(18)=268,25<br> | ||
| + | f(50)= 156,25 | ||
| + | |||
| + | c) Hier muss man den Scheitel der Parabel finden. Dies macht man für den Term <math>\frac{3}{16} x^2 - \frac{65}{4}x+500</math> durch [http://medienvielfalt.zum.de/wiki/Quadratische_Funktionen_2_-_quadratische_Erg%C3%A4nzung quadratische Ergänzung]. <br> | ||
| + | <math>\frac{3}{16} x^2 - \frac{65}{4}x+500=\frac{3}{16}(x^2 - 86\frac{2}{3}x)+500=\frac{3}{16}[(x - 43\frac{1}{3})^2 -(43\frac{1}{3})^2]+500=\frac{3}{16}(x - 43\frac{1}{3})^2-\frac{3}{16}\cdot 43\frac{1}{3})^2+500 = \frac{3}{16}(x - 43\frac{1}{3})^2 + 147\frac{11}{121}</math><br> | ||
| + | Man liest die Scheitelkoordinaten ab zu <math>x_S=43\frac{1}{3}</math> und <math>y_S=147\frac{11}{121}</math>. Es ist also <math>f(43\frac{1}{3})=147\frac{11}{121}</math> | ||
| + | |||
| + | 2a) Es ergibt sich f(x) = 0,05x<sup>2</sup> -10,5x + 650 (Tagfunktion)<br> | ||
| + | b) Es ergibt sich f(x) = 0,1875x<sup>2</sup> -33,75x + 1750 (Nachtfunktion)<br> | ||
| + | [[Datei:96-5.jpg|500px]]<br> | ||
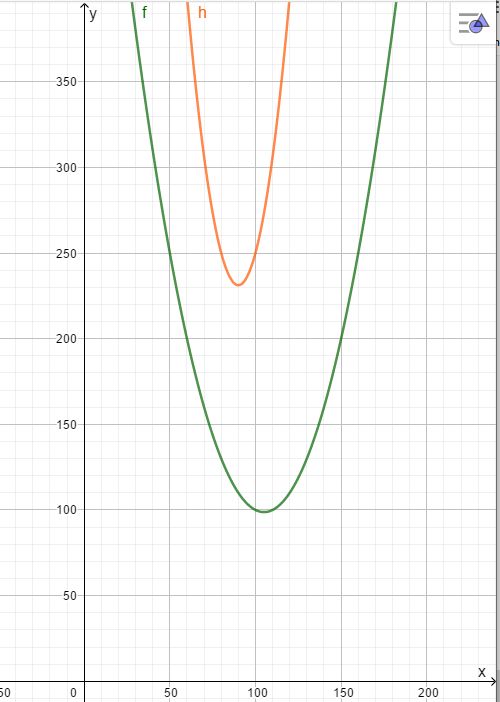
| + | Grün ist der Graph der Tagfunktion, rot der Graph der Nachtfunktion. Aus dem Diagramm, aber auch aus den gegebenen Werten sieht man, dass sich nachts deutlich mehr (gut doppelt soviele) Unfälle ereignen wie tags. }} | ||
| + | |||
| + | {{Aufgaben-blau|5|2=1. Britte, Merlin und Tina wollen zusammen in einer Diskothek gehen. Voraussetzung ist ein Mindestalter von 16 Jahren. <br> | ||
| + | Zusammen sind sie 50 Jahre alt. Merlin und Tina sind zusammen 20 Jahre älter als Britta, Britta und Tina sind zusammen 14 Jahre älter als Merlin. <br> | ||
| + | Wer kommt bei der Ausweiskontrolle nicht in die Diskothek? | ||
| + | |||
| + | 2. Ina bezahlt für drei 100-g-Tafeln Nussschokolade und zwei 100-g-Tafeln Noutgatschokolade 4,80€.<br> | ||
| + | Luca bezahlt für zehn 100-g-Tafeln der gleichen Nussschokolade und vier 100-g-Tafeln der gleichen Noutgatschokolade 13,20€.<br> | ||
| + | Sophia bezahlt für eine 100-g-Tafeln der gleichen Nussschokolade, eine 100-g-Tafeln der gleichen Noutgatschokolade und zwei 100-g-Tafeln Vollmilchschokolade 2,95€.<br> | ||
| + | Was kostet eine 100-g-Tafel jeder dieser drei Schokoladensorten.}} | ||
| + | |||
| + | {{Lösung versteckt|1=1. Britta ist 15, Merlin 18 und Tina 17, also kommt Britta nicht in die Disko. | ||
| + | |||
| + | 2. Eine Tafel Nusschokolade kostet 0,90€.<br> | ||
| + | Eine Tafel Nougatschokolade kostet 1,05€.<br> | ||
| + | Eine Tafel Vollmichschokolade kostet 0,50€ }} | ||
Aktuelle Version vom 18. Februar 2022, 15:54 Uhr
In der 8. Klasse hast du gelernt lineare Gleichungssysteme von zwei Gleichungen mit zwei Unbekannten zu lösen. Schau dir zur Wiederholung wie das geht dieses Video an:
Wir brauchen diese Verfahren um folgendes Problem zu lösen. Wir haben Punkte und wollen schauen, ob die Punkte auf einer Parabel liegen.
Ein Tourist schreibt aus St. Louis (USA) eine Ansichtskarte nach Hause.
Er beschreibt die besonderheit des Gateway Arch, dass die Breite unten am Fuß genauso groß ist wie die Höhe des Bauwerks, nämlich 192m. Und es erinnert ihn sehr an eine Parabel.
Legt man in den linken unteren Fußpunkt den Ursprung eines Koordinatensystems, so ist der rechte Fußpunkt bei (192;0) und der Scheitel S(96;192).
Mit der Scheitelform der Parabelgleichung erhält man sofort 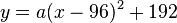 .
.
Nun muss man noch a bestimmen. Dazu verwendet man den linken Fußpunkt (0;0). Setzt man die Koordinatenwerte in die Gleichung ein, dann hat man 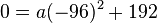 und es ergibt sich
und es ergibt sich 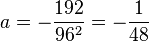 .
.
Also erhält man als Parabelgleichung 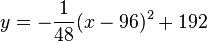
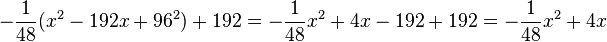 , also
, also 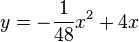 .
.
Wenn der Scheitel S und eine Nullstelle gegeben ist kann man mit der Scheitelform relativ leicht eine Parabelgleichung angeben.
Was macht man aber, wenn man nur drei Punkte A, B und C gegeben hat.
1. Beispiel: Gegeben sind die drei Punkte A(0;0), B(2;4) und C(3;9).
Da du fit bei den quadratischen Funktionen bist sieht du sofort, dass die Punkte auf dem Graph der Funktion 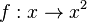 , der Normalparabel liegen.
, der Normalparabel liegen.
Wenn du es nicht sofort sieht, dann mach folgende Überlegung mit.
Wir wollen schauen, ob es eine Parabel gibt, auf der die drei Punkte liegen. Eine Parabel hat die Gleichung 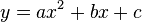 . Wenn wir die Koordinaten der drei Punkte jeweils einsetzen, dann erhalten wir drei Gleichungen:
. Wenn wir die Koordinaten der drei Punkte jeweils einsetzen, dann erhalten wir drei Gleichungen:
Punkt A(0;0) --> 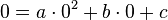
Punkt B(2;4) --> 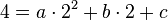
Punkt C(3;9) --> 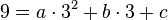 .
.
Wir müssen also die Koeffizienten a, b, c der Parabelgleichung bestimmen und dafür stehen uns die drei Gleichungen zur Verfügung.
Aus der 1. Gleichung für A erhält man sofort 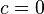 . Also hat man nur noch zwei Gleichungen in die wir für c auch 0 gleich einsetzen.
. Also hat man nur noch zwei Gleichungen in die wir für c auch 0 gleich einsetzen.
Punkt B --> 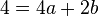
Punkt C --> 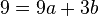
Dividiert man die Gleichung von B durch 2 und löst sie nach b auf, dann erhält man 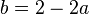 .
.
Setzt man dies für b in die Gleichung von C ein, dann muss man die Gleichung 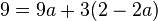 lösen.
lösen.
Klammern auflösen und alles mit a auf die linke Seite und alles ohne a auf rechte Seite bringen: 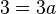
Die Seiten vertauschen und durch den Koeffizienten von a teilen, liefert 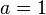
Damit ist dann 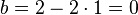 und die Gleichung der Parabel ist
und die Gleichung der Parabel ist 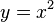
2. Beispiel: Gegeben sind die drei Punkte A(0;2), B(4;18) und C(-1;8).
Hier sieht man, auch wenn man fit bei den quadratischen Funktionen ist, nicht sofort die Funktions- bzw. Parabelgleichung.
Aber das Verfahren, das wir gerade kennengelernt haben funktioniert auch hier.
Da wir die Funktionsgleichung nicht kennen, machen wir den allgemeinen Ansatz 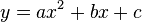 und setzen jeweils die Koordinten der drei Punkte ein.
und setzen jeweils die Koordinten der drei Punkte ein.
Punkt A/0;2) --> 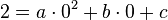
Punkt B(4;18) --> 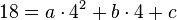
Punkte C(-1;8) --> 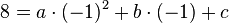
Aus der Gleichung für A erhält man auch hier sofort 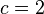 . Diesen Wert 2 für c setzen wir in die anderen zwei Gleichungen ein.
. Diesen Wert 2 für c setzen wir in die anderen zwei Gleichungen ein.
Punkt B --> 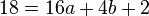
Punkt C --> 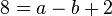
Nun fassst man die beiden Gleichungen zusammen
B: 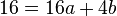
C: 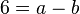
Nun kann man die Gleichung von B durch 4 teilen und nach b auf lösen und hat dann 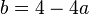 . Setzt man dies in die Gleichung für C ein, dann hat man
. Setzt man dies in die Gleichung für C ein, dann hat man 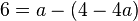 . Da vor b ein - steht, macht man um 4-4a Klammern!
. Da vor b ein - steht, macht man um 4-4a Klammern!
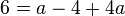 -->
--> 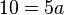 -->
--> 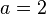
Damit ist dann 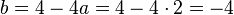
Die Funktionsgleichung bzw. die Gleichung der Parabel ist 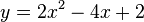
3. Beispiel: Gegeben sind die zwei Punkte P(0;0), S(0,5;1,5), wobei S der Scheitelpunkt ist.
Hier sind nur zwei Punkte gegeben, aber der Scheitel ist dabei. Damit könnten wir es mit der Scheitelform machen.
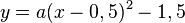 und
und 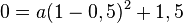 .
.
Die zweite Gleichung liefert 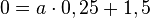 und
und 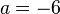 .
.
Also ist die Parabelgleichung 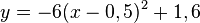 oder
oder 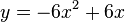
Es geht aber auch mit der Methode, die wir gerade kennengelernt haben. Der allgemeine Ansatz ist wieder 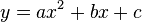
Punkt P(0;0) --> 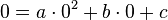
Punkt S(0,5;1,5) --> 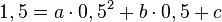
Aus der Gleichung für P erhält man 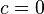 . Dies setzt man in die Gleichung von S ein.
. Dies setzt man in die Gleichung von S ein.
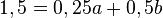 .
.
Nun hat man aber eine Gleichung aber mit zwei Unbekannten. Wie soll man das lösen? Dafür gibt es unendlich viele Lösungen.
Nun erinnert man sich, dass diese Parabel noch eine zweite Nullstelle hat. Die x-Koordinate von S liegt in der Mitte der beiden Nullstellen, also ist die zweite Nullstelle Q(1;0) und damit hat man eine dritte Gleichung.
Punkt Q --> 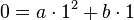 .
.
Nun muss man folgendes Gleichungssystem aus zwei Gleichungen mit zwei Unbekannten a und b lösen.
P --> 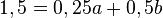
Q --> 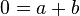
Man löst die Glelichung für Q nach a auf --> 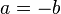 und setzt dies in die Gleichung für P ein.
und setzt dies in die Gleichung für P ein.
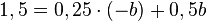 -->
--> 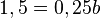 und b
und b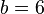 .
.
Damit ist 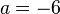 und die Gleichung der Parabel
und die Gleichung der Parabel 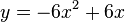 , also das selbe Ergebnis wie oben.
, also das selbe Ergebnis wie oben.
4. Beispiel: Gegeben sind die Punkte A(-1;7), B(2;1) und C(4;17).
Hier stellt man wieder zum allgemeinen Ansatz 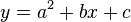 drei Gleichungen auf.
drei Gleichungen auf.
A --> 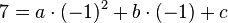
B --> 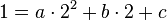
c --> 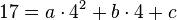
Wenn man etwas geübter ist kann man auch gleich die Quadrate ausrechnen und in der üblichen Schreibeweise, dass die Zahlen vor den Unbekannten stehen hinschreiben.
A --> 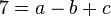
B --> 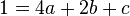
c --> 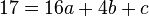
Hier hat man nicht die schöne Situation wie in den bisherigen Beispielen, dass man sofort c erhält.
Dafür löst man die Gleichung von A nach c auf und setzt den Term, den man erhält in die anderen zwei Gleichungen ein.
Man sagt dafür: Man eliminiert c.
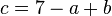 in die andern zwei Gleichungen einsetzen:
in die andern zwei Gleichungen einsetzen:
B --> 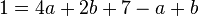
C --> 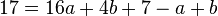
Da in den zwei Gleichungen jeweils +c steht, muss man um den Term 7-a+b keine Klammern machen!
Die zwei Gleichungen vereinfacht man nun und löst dann das Gleichungssystem:
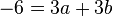
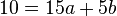
Dividiert man die erste Gleichung durch 3 und löst sie nach b auf, erhält man 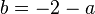 .
.
Dies setzt man in die zweite Gleichung ein: 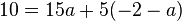 . Die Gleichung nach a aufgelöst ergibt
. Die Gleichung nach a aufgelöst ergibt 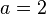 .
.
Für b erhält man dann 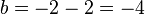 und für c ergibt sich
und für c ergibt sich 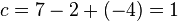 .
.
Die Funktionsgleichung bzw. die Gleichung der Parabel ist 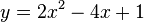 .
.
|
Merke:
Ein Gleichungssysten mit drei Gleichungen und drei Unbekannten löst man schrittweise: 1. Man löst eine Gleichung nach einer Unbekannten auf und setzt den Term, den man für diese Unbekannte erhält in die anderen zwei Gleichungen ein. 2. Nun hat man zwei Gleichungen mit zwei Unbekannten, welches man (mit einem der bekannten Verfahren) löst. 3. Mit den Lösungen, die man gerade erhalten hat, berechnet man den Wert der dritten (eliminierten) Unbekannten. |
Wenn du dir die 4 Beispiele oben anschaust, dann siehst du, dass wir jeweils nach diesem Verfahren vorgegangen sind. Bei den ersten drei Beispielen hat man den Wert für c gleich erhalten und man hat sich den 3. Punkt des Merksatzes gespart. Im 4. Beispiel kam man so zur Lösung.
Lustig: Etwas einfacher geht es hier zu. Das lässt sich im Kopf lösen.
In der 8. Klasse hatten wir Gleichungssysteme etwas anders notiert.
(1) x + y = 1
(2) x + 2y = 2
hat die Lösungen x = 0 und y = 1. Die Gleichungen wurden durchnummeriert.
Das macht man jetzt auch.
(1) 6x + y - 3z = 9
(2) 2x + 2y - z = 3
(3) 5x - 4y - 4z = 0
Zur Lösung löst man z.B. die Gleichung (2) nach z auf: z = 2x + 2y - 3 und setzt dies für z in die anderen zwei Gleichungen ein.
(1) 6x + y - 3(2x + 2y -3) = 9
(3) 5x - 4y - 4(2x + 2y -3) = 0
Nun löst man in beiden Gleichungen die Klammern auf uns vereinfacht.
(1) -5y = 0
(3) -3x -12y +12 = 0
Gleichung (1) liefert y = 0. Eingesetzt in (3) ist x = 4.
z ergibt sich dann z = 8 + 0 - 3 = 5. Also hat das Gleichungssystem die Lösungen x = 4, y = 0 und z = 5.
30px Merke
Welche Unbekannte du zuerst eliminierst bleibt dir überlassen. Tipp: Nimm eine Unbekannte mit Koeffizient 1. Welches Verfahren (Einsetzverfahren, Gleichsetzverfahren, Additionsverfahren) du dann zum Lösen der zwei Gleichungen mit den verbliebenen zwei Unbekannten wählst bleibt auch dir überlassen. Tipp: Nimm das, bei dem du dich am sichersten fühlt. |
1a) x = 1, y = 2, z = 5
b) x = 2, y = 2, z = 4 oder x = -2, y = 2, z = 0
c) x = 18, y = 16, Z = 66
d) x = 1, y = 4, z = 4
e) x = 5, y = -3, z = 1
f) x = -18, y = -3, z = -4
2a) x = 4, y = 0, z = 5
b) x = 3, y = 4, z = 5
Man erhält die Lösungen, indem man z.B. so vorgeht:
Gleichung (1) nach z auflösen: z=12 - x - y und diesen Term für z in (2) und (3) einsetzen.
(2) x - y + (12 - x - y) = 4
(3) x - y - (12 - x - y) = -6
Zusammenfassen:
(2) -2y = -8
(3) 2x = 6
(2) ergibt y = 4 und (3) ergibt x = 3. Für z erhält man z = 12 - 3 - 4 = 5.
c) x = 1, y = -2, z = 4
Da (2) die einzige Gleichung ist, in der z mit Koeffizient 1 vorkommt, löst man (2) nach z auf: z = 5x - y - 3.
Einsetzen:
(1) 2x - 2y + 3(5x - y - 3) = 18
(3) 12x + 4y - 2(5x - y - 3) = -4
Zusammenfassen:
(1) 17x - 5y = 27
(3) 2x + 6y = - 10
(3) nach x auflösen ergibt x = -5 - 3y.
in (1) einsetzen:
(1) 17(-5 - 3y) - 5y = 27
-56y = 112 ergibt y = -2, x = 1 und z = 4.
d) x = -2, y = -1, z = -3
e) x = 1, y = 1, z = 1
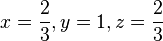
a) y = 2x2 - 4x + 2 , das war das 2. Beispiel oben!
b) a = -1, b = 0, c = 4, also y = -x2 + 4
c) 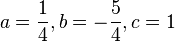 , also y = 0,25x2 - 1,25x + 1
, also y = 0,25x2 - 1,25x + 1
d) a = -3, b = 0, c = 3, also y = -3x2 + 3
Damit die drei Punkte auf keiner Parabel liegen, muss der Punkt C* auf der Geraden AB liegen.
a) Die Gerade AB hat die Gleichung y = 4x + 2. Zum Beispiel liegt C*(2;10) auf der Geraden.
b) Die Gerade AB hat die Gleichung y = x + 2. Zum Beispiel liegt C*(3;5) auf der Geraden.
c) Die Gerade AB hat die Gleichung y = -0,5x + 0,5. Zum Beispiel liegt C*(0;0,5) auf der Geraden.
Ausblick: In diesem Video
wird genauso wie bei uns ein Gleichungssystem mit drei Gleichungen und den Unbekannten a, b und c aufgestellt. Doch dann wird diese Gleichungssystem mit dem Additionsverfahren, so wie wir es in der 8. Klasse kennengelernt haben gelöst. Das bietet sich aber auch nur hier an, weil die Gleichungen (1) und (2) sehr, sehr ähnlich sind und man damit die Lösung für b leicht erhält.
1a) allgemeiner Ansatz 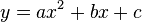 liefert drei Gleichungen
liefert drei Gleichungen
(1) 250 = 400a + 20b + c
(2) 150 = 1600a + 40b + c
(3) 200= 3600a + 60b + c
Löst man (1) nach c auf, so erhält man c = 250 - 400a -20b und setzt den Term für c in die Gleichungen (2) und (3), so erhält man
(2) 150 = 1600a + 40b + 250 -400a -20b
(3) 200 = 3600a + 60b + 250 -400a -20b
Zusammenfassen:
(2) -100 = 1200a + 20b
(3) -50 = 3200a + 40b
Mit dem Additionsverfahren 2·(2)-(3):
-150 = -800a liefert 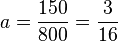
Setzt man 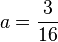 in (2), so ist
in (2), so ist 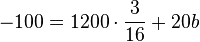
Zusammenfassen: -100 = 225 + 20b ergibt nach b aufgelöst 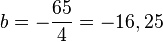 .
.
Für c erhält man 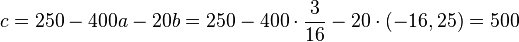
Also ist die Funktion 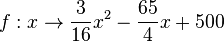 .
.
b) f(18)=268,25
f(50)= 156,25
c) Hier muss man den Scheitel der Parabel finden. Dies macht man für den Term 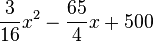 durch quadratische Ergänzung.
durch quadratische Ergänzung.
![\frac{3}{16} x^2 - \frac{65}{4}x+500=\frac{3}{16}(x^2 - 86\frac{2}{3}x)+500=\frac{3}{16}[(x - 43\frac{1}{3})^2 -(43\frac{1}{3})^2]+500=\frac{3}{16}(x - 43\frac{1}{3})^2-\frac{3}{16}\cdot 43\frac{1}{3})^2+500 = \frac{3}{16}(x - 43\frac{1}{3})^2 + 147\frac{11}{121}](/images/math/d/7/4/d74ac8635ee0c3ac946df869070db4c1.png)
Man liest die Scheitelkoordinaten ab zu 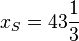 und
und 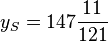 . Es ist also
. Es ist also 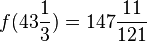
2a) Es ergibt sich f(x) = 0,05x2 -10,5x + 650 (Tagfunktion)
b) Es ergibt sich f(x) = 0,1875x2 -33,75x + 1750 (Nachtfunktion)
1. Britta ist 15, Merlin 18 und Tina 17, also kommt Britta nicht in die Disko.
2. Eine Tafel Nusschokolade kostet 0,90€.
Eine Tafel Nougatschokolade kostet 1,05€.


