Ph10-Von der Schwingung zur Welle: Unterschied zwischen den Versionen
| (19 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
Man kann sich auch folgendes vorstellen. Im Stadion steht eine Person auf, hebt die Hände hoch, bleibt ein paar Sekunden stehen und setzt sich wieder. Die Person wiederholt dies alle zwei Minuten. Alle anderen Personen im Stadion bleiben sitzen. Was ist hier nun anders? Die Person macht auch hier wie bei der la-Ola-Welle eine periodische Bewegung, die man als "Schwingung" bezeichnen könnte. Aber niemand anderes macht mit. Die eine Person macht an ihrem Ort eine Bewegung, die Umgebung bleibt in Ruhe.<br> | Man kann sich auch folgendes vorstellen. Im Stadion steht eine Person auf, hebt die Hände hoch, bleibt ein paar Sekunden stehen und setzt sich wieder. Die Person wiederholt dies alle zwei Minuten. Alle anderen Personen im Stadion bleiben sitzen. Was ist hier nun anders? Die Person macht auch hier wie bei der la-Ola-Welle eine periodische Bewegung, die man als "Schwingung" bezeichnen könnte. Aber niemand anderes macht mit. Die eine Person macht an ihrem Ort eine Bewegung, die Umgebung bleibt in Ruhe.<br> | ||
| − | Bei der la-Ola-Welle machen die Nachbarn vor ihm etwas zeitversetzt vorher die gleiche Bewegung und die Nachbarn nach ihm ebenfalls zeitversetzt nach ihm auch die gleiche Bewegung. Die "Schwingung" setzt sich dadurch fort und es entsteht eine Welle. | + | Bei der la-Ola-Welle machen die Nachbarn vor ihm etwas zeitversetzt vorher die gleiche Bewegung und die Nachbarn nach ihm ebenfalls zeitversetzt nach ihm auch die gleiche Bewegung. Die "Schwingung" setzt sich dadurch fort und es entsteht eine Welle. Ohne Nachbarn keine la-Ola-Welle. |
| Zeile 17: | Zeile 17: | ||
{{Aufgaben-blau|2|2=Übertrage deine Beobachtungen von der la-Ola-Welle auf das "Schunkelvideo".}} | {{Aufgaben-blau|2|2=Übertrage deine Beobachtungen von der la-Ola-Welle auf das "Schunkelvideo".}} | ||
| − | {{Lösung versteckt|Eine Person macht eine hin-und-her-Bewegung. Sie macht eine Schwingung. Dadurch, dass sie die anderen Personen anstößt machen diese Personen mit und machen ebenfalls eine Schwingung. Alle Schwingungen von allen Personen ergeben eine Welle.}} | + | {{Lösung versteckt|Eine Person macht eine hin-und-her-Bewegung. Sie macht eine Schwingung. Dadurch, dass sie die anderen Personen anstößt machen diese Personen mit und machen ebenfalls eine Schwingung. Alle Schwingungen von allen Personen ergeben eine Welle. |
| + | |||
| + | Auch hier ist es so, dass wenn nur einer schunkelt und alle anderen ruhig sitzen bleiben, dann rempelt er zwar seine zwei Nachbarn dauern an, was sie aber nicht stört. Der Schunkler macht eine "Schwingung", diese wird aber nicht fortgesetzt. Nur wenn die anderen mitmachen und sich durch Unterhaken sehr gut koppeln, dann entsteht einen Welle.}} | ||
{{Merksatz|MERK='''Eine Welle ist eine sich räumlich ausbreitende Schwingung.''' | {{Merksatz|MERK='''Eine Welle ist eine sich räumlich ausbreitende Schwingung.''' | ||
| − | Bei der la-Ola-Welle ist es die räumliche Ausbreitung einer einmaligen Störung, beim Schunkeln bewegen sich alle Personen synchron um ihre Gleichgewichtslage. | + | Bei der la-Ola-Welle ist es die räumliche Ausbreitung einer einmaligen Störung, beim Schunkeln bewegen sich alle Personen synchron um ihre Gleichgewichtslage, die Schwingung breitet sich also auch hier räumlich aus. |
'''Eine Welle ist also eine sich räumlich ausbreitende periodische Bewegung aus dem Gleichgewichtszustand oder auch eine einmalige Veränderung des Gleichgewichtszustands eines Systems.'''}} | '''Eine Welle ist also eine sich räumlich ausbreitende periodische Bewegung aus dem Gleichgewichtszustand oder auch eine einmalige Veränderung des Gleichgewichtszustands eines Systems.'''}} | ||
| Zeile 49: | Zeile 51: | ||
Damit eine Welle entsteht muss eine Schwingung eines Körpers da sein, die sich auf seine Nachbarkörper überträgt. So etwas bezeichnet man dann als '''gekoppelte Schwingung'''. <br> | Damit eine Welle entsteht muss eine Schwingung eines Körpers da sein, die sich auf seine Nachbarkörper überträgt. So etwas bezeichnet man dann als '''gekoppelte Schwingung'''. <br> | ||
Diese Kopplung ist bei der '''la-Ola-Welle''' nicht erkennbar, aber vorhanden.<br> | Diese Kopplung ist bei der '''la-Ola-Welle''' nicht erkennbar, aber vorhanden.<br> | ||
| − | Beim '''Schunkeln''' entsteht die Kopplung durch das | + | Beim '''Schunkeln''' entsteht die Kopplung durch das Anrempeln des Nachbarn. Die Kopplung ist richtig gut, wenn man sich mit den Armen unterhakt.<br> |
Bei '''Wasserwellen''' werden Wassermoleküle aus ihrer Ruhelage (ruhige Wasseroberfläche) ausgelenkt. <br> | Bei '''Wasserwellen''' werden Wassermoleküle aus ihrer Ruhelage (ruhige Wasseroberfläche) ausgelenkt. <br> | ||
'''Schallwellen''' breiten sich in Medien aus, dort schwingen Atome oder Moleküle, z.B. Eisenatome in Stahl, Stickstoff- und Sauerstoffmoleküle in der Luft, Wassermoleküle im Wasser.<br> | '''Schallwellen''' breiten sich in Medien aus, dort schwingen Atome oder Moleküle, z.B. Eisenatome in Stahl, Stickstoff- und Sauerstoffmoleküle in der Luft, Wassermoleküle im Wasser.<br> | ||
| Zeile 80: | Zeile 82: | ||
Am Anfang haben wir festgestellt, dass eine Welle eine sich ausbreitende Störung (la-Ola-Welle) oder Schwingung (Schunkeln) ist. Die Geschwindigkeit, mit der sich die Störung bzw. ein Wellenberg (maximale Auslenkung der Schwingung) im Medium ausbreitet, nennt man '''Ausbreitungsgeschwindigkeit c der Welle'''. (Beachte, dass hier der Buchstabe c verwendet wird!)<br> | Am Anfang haben wir festgestellt, dass eine Welle eine sich ausbreitende Störung (la-Ola-Welle) oder Schwingung (Schunkeln) ist. Die Geschwindigkeit, mit der sich die Störung bzw. ein Wellenberg (maximale Auslenkung der Schwingung) im Medium ausbreitet, nennt man '''Ausbreitungsgeschwindigkeit c der Welle'''. (Beachte, dass hier der Buchstabe c verwendet wird!)<br> | ||
| − | [[File:Wave phase.gif]] Der rote Punkt ist immer am Wellenberg und | + | Für die la-Ola-Welle ist die Ausbreitungsgeschwindigkeit die Geschwindigkeit mit der sich die Störung ausbreitet.<br> |
| + | [[File:Wave phase.gif]] Der rote Punkt ist immer am Wellenberg und seine Geschwindigkeit ist die Ausbreitungsgeschwindigkeit der Welle.<br> | ||
| + | Man muss für die Ausbreitungsgeschwindigkeit nicht einen Wellenberg nehmen, sondern es man kann jeden Punkt nehmen, also in dem Bild fixiert man irgendeinen Punkt auf der Sinuslinie und betrachtet dessen Ausbreitung. Da ein Wellenberg ein sehr markanter Punkt ist, hat er hier diese Sonderstellung. | ||
| Zeile 86: | Zeile 90: | ||
<center>[[File:Frontgroupphase.gif|400px]]</center> }} | <center>[[File:Frontgroupphase.gif|400px]]</center> }} | ||
| − | {{Lösung versteckt|Die Ausbreitungsgeschwindigkeit der Störung wird durch den grünen Punkt dargestellt.}} | + | {{Lösung versteckt|Die Ausbreitungsgeschwindigkeit der Störung wird durch den grünen und roten Punkt dargestellt. <br> |
| + | Der grüne Punkt entspricht dem "Wellenberg" der Störung .<br> | ||
| + | Der rote Punkt ist der Beginn der Störung. <br> | ||
| + | |||
| + | Die Amplitude der Störung nimmt sehr schnell ab, also ist die Welle in einem Medium mit großer Dämpfung.}} | ||
| + | |||
| + | |||
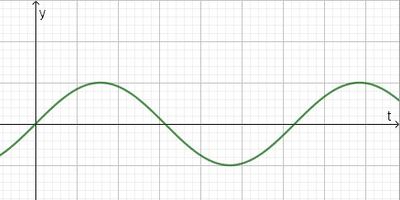
| + | {{Aufgaben-blau|8|Was ist der Unterschied bei diesen zwei Diagrammen?<br> | ||
| + | Diagramm 1: [[Datei:Sin-schwingung.jpg|400px]]<br> | ||
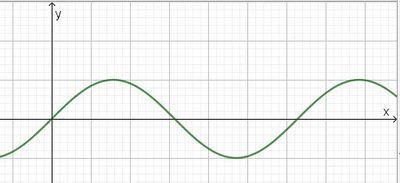
| + | Diagramm 2: [[Datei:Sin-welle.jpg|400px]] }} | ||
| + | |||
| + | {{Lösung versteckt|Das Diagramm 1 ist ein ty-Diagramm. Über der Zeit t wird der Ort y aufgetragen. Dies ist das Diagramm einer Schwingung.<br> | ||
| + | Das Diagramm 2 ist ein xy-Diagramm. Über dem Ort x wird der Ort y aufgetragen. Dies ist das Diagramm einer Welle.}} | ||
| + | |||
| + | |||
| + | Eine Welle wird durch eine Sinusschwingung angeregt. Es breitet sich dann eine sinusförmige Welle aus. Die Schwingungsdauer der Erregerschwingung ist T, seine Frequenz f. In der Zeit T breitet sich die Welle aus. Der Weg, den ein Wellenberg in der Zeit t zurücklegt ist die '''Wellenlänge <math>\lambda</math>''' der Welle. | ||
| + | |||
| + | <center>[[Datei:Sin-welle-lambda.jpg|500px]]</center> | ||
| + | |||
| + | {{Merksatz|MERK=Die Wellenlänge einer periodischen Welle ist der kleinste Abstand zweier Wellenberg. }} | ||
| + | |||
| + | Man kann auch sagen, wenn man einen beliebigen Punkt der Welle nimmt, dass die Wellenlänge der kleinste Abstand zweier Punkte gleicher Phase ist. Dabei bedeutet gleiche Phase, dass der andere Punkt um <math>\lambda</math> versetzt die gleiche Bewegung wie der ursprüngliche Punkt macht. | ||
| + | |||
| + | <center>[[File:Sinuswelle zur verdeutlichung von Wellenlaenge.svg|600px]]</center> | ||
| + | |||
| + | |||
| + | {{Aufgaben-blau|9|2=1. Welcher Zusammenhang besteht zwischen der Schwingungsdauer T und der Frequenz f einer Schwingung? | ||
| + | |||
| + | 2. Zeige, dass für die Ausbreitungsgeschwindigkeit c der Welle gilt: <math> c = \lambda \cdot f</math>. }} | ||
| + | |||
| + | |||
| + | {{Lösung versteckt|1=1. Es ist <math>f = \frac{1}{T}</math>.<br> | ||
| + | 2. In der Zeit t = T legt der Wellenberg den Weg <math>x = \lambda</math> zurück. <br> | ||
| + | Die Ausbreitungsgeschwindigkeit c der Welle ist dann <math>c = \frac{x}{t}=\frac{\lambda}{T}=\lambda \cdot f</math>. }} | ||
| + | |||
| + | |||
| + | {{Merksatz|MERK=Für eine Welle der Wellenlänge <math>\lambda</math> und der Frequenz <math>f</math> gilt: <math>c = \lambda \cdot f</math>. }} | ||
| + | |||
| + | {{Übung|1=1. Welche Frequenz hat rotes Licht der Wellenlänge <math>\lambda</math> = 700 nm? (1 nm = 10<sup>-9</sup>m)<br> | ||
| + | 2. Welche Wellenlänge hat der Kammerton a mit f = 440 Hz? }} | ||
| + | |||
| + | {{Lösung versteckt|1=1. <math>f = \frac{c}{\lambda}=\frac{3 \cdot 10^8 \frac{m}{s}}{700 \cdot 10^{-9} m}= 4,3 \cdot 10^{14} Hz</math><br> | ||
| + | 2. <math>\lambda = \frac{c}{f}= \frac{334 \frac{m}{s}}{440 \frac{1}{s}}=0,76 m</math> }} | ||
| + | |||
| + | |||
| + | Ein Wassertropfen fällt auf eine Wasseroberfläche und erzeugt eine Welle, die sich kreisförmig ausbreitet. <br> | ||
| + | <center>[[Datei:2006-01-14_Surface_waves.jpg|400px]]</center><br> | ||
| + | Diese Wasserwelle wird durch den Wassertropfen erzeugt und breitet sich im Idealfall in konzentrischen Kreisen vom Auftreffpunkt (=Mittelpunkt der konzentrischen Kreise) sinusförmig aus. Jeder Punkt in der Nähe des Auftreffpunktes macht dann nach Anregung eine gedämpfte Sinusschwingung. Zwischen der Erregerschwingung und der Schwinung eines Punktes auf der Wasseroberfläche besteht eine Phasendifferenz. Alle Punkte, die gleichweit vom Erregerzentrum entfernt sind, schwingen in Phase und bilden die '''Wellenfront'''. | ||
| + | |||
| + | Wellenfronten einer sich geradlinig ausbreitender Transversalwelle: [[Datei:Wellenfront-1.svg|300px]]<br> | ||
| + | Wellenfronten einer Kreiswelle: [[Datei:Wellenfront-2.svg|200px]] | ||
| + | |||
| + | |||
| + | Auf den Seiten [https://www.leifiphysik.de/mechanik/mechanische-wellen/grundwissen/wellen Seite 1] und [https://www.leifiphysik.de/mechanik/mechanische-wellen/grundwissen/wellentypen Seite 2] von Leifiphysik ist dieses Grundwissen über Wellen nochmals mit schönen Bildern und Animationen zusammengefasst. | ||
| + | |||
| + | {{Aufgaben-blau|10|2=1. Schaue dir die Größen, die eine Welle beschreiben auf dieser [https://www.leifiphysik.de/mechanik/mechanische-wellen/grundwissen/groessen-zur-beschreibung-einer-welle dieser Seite] an und notiere sie dir. | ||
| + | |||
| + | 2. Mache das [https://www.leifiphysik.de/mechanik/mechanische-wellen/aufgabe/quiz-zu-mechanischen-wellen Quiz]. | ||
| − | + | 3. Bearbeite diese Aufgaben: [https://www.leifiphysik.de/mechanik/mechanische-wellen/aufgabe/mann-am-meer Aufgabe 1], [https://www.leifiphysik.de/mechanik/mechanische-wellen/aufgabe/ausbreitung-einer-wasserwelle Aufgabe 2], [https://www.leifiphysik.de/mechanik/mechanische-wellen/aufgabe/seilwelle Aufgabe 3] und [https://www.leifiphysik.de/mechanik/mechanische-wellen/aufgabe/wellengroessen Aufgabe 4]. }} | |
Aktuelle Version vom 2. Mai 2022, 09:45 Uhr
Man kann sich auch folgendes vorstellen. Im Stadion steht eine Person auf, hebt die Hände hoch, bleibt ein paar Sekunden stehen und setzt sich wieder. Die Person wiederholt dies alle zwei Minuten. Alle anderen Personen im Stadion bleiben sitzen. Was ist hier nun anders? Die Person macht auch hier wie bei der la-Ola-Welle eine periodische Bewegung, die man als "Schwingung" bezeichnen könnte. Aber niemand anderes macht mit. Die eine Person macht an ihrem Ort eine Bewegung, die Umgebung bleibt in Ruhe.
Bei der la-Ola-Welle machen die Nachbarn vor ihm etwas zeitversetzt vorher die gleiche Bewegung und die Nachbarn nach ihm ebenfalls zeitversetzt nach ihm auch die gleiche Bewegung. Die "Schwingung" setzt sich dadurch fort und es entsteht eine Welle. Ohne Nachbarn keine la-Ola-Welle.
30px Merke
Eine Schwingung ist eine lokale Bewegung, die an einem Ort erfolgt. Bei der la-Ola-Welle bewegen sich einzelne Menschen auf und ab,. Jede Person macht eine hinauf-hinab Bewegung, sie schwingt und macht diese Bewegung zeitversetzt zu seinem Nachbarn. Jede Person verlässt ihren Platz nicht, macht also lokal ihr Schwingung. |
Ein zweites Beispiel siehst du hier:
Eine Person macht eine hin-und-her-Bewegung. Sie macht eine Schwingung. Dadurch, dass sie die anderen Personen anstößt machen diese Personen mit und machen ebenfalls eine Schwingung. Alle Schwingungen von allen Personen ergeben eine Welle.
Auch hier ist es so, dass wenn nur einer schunkelt und alle anderen ruhig sitzen bleiben, dann rempelt er zwar seine zwei Nachbarn dauern an, was sie aber nicht stört. Der Schunkler macht eine "Schwingung", diese wird aber nicht fortgesetzt. Nur wenn die anderen mitmachen und sich durch Unterhaken sehr gut koppeln, dann entsteht einen Welle.
|
Merke:
Eine Welle ist eine sich räumlich ausbreitende Schwingung. Bei der la-Ola-Welle ist es die räumliche Ausbreitung einer einmaligen Störung, beim Schunkeln bewegen sich alle Personen synchron um ihre Gleichgewichtslage, die Schwingung breitet sich also auch hier räumlich aus. Eine Welle ist also eine sich räumlich ausbreitende periodische Bewegung aus dem Gleichgewichtszustand oder auch eine einmalige Veränderung des Gleichgewichtszustands eines Systems. |
Auf dieser Seite siehst du die Entstehung einer Welle aus einer Schwingung.
Eine Schwingung erfolgt an einem Platz. Ein Körper wird aus seiner Gleichgewichtslage ausgelenkt und schwingt um diese Gleichgewichtslage. Die Schwingung findet lokal statt.
- Wasserwellen
- Schallwellen
- Lichtwellen
- Radio- und Fernsehwellen
- Mikrowellen
- ...
Damit eine Welle entsteht muss eine Schwingung eines Körpers da sein, die sich auf seine Nachbarkörper überträgt. So etwas bezeichnet man dann als gekoppelte Schwingung.
Diese Kopplung ist bei der la-Ola-Welle nicht erkennbar, aber vorhanden.
Beim Schunkeln entsteht die Kopplung durch das Anrempeln des Nachbarn. Die Kopplung ist richtig gut, wenn man sich mit den Armen unterhakt.
Bei Wasserwellen werden Wassermoleküle aus ihrer Ruhelage (ruhige Wasseroberfläche) ausgelenkt.
Schallwellen breiten sich in Medien aus, dort schwingen Atome oder Moleküle, z.B. Eisenatome in Stahl, Stickstoff- und Sauerstoffmoleküle in der Luft, Wassermoleküle im Wasser.
Licht wird als Welle beschrieben. Seine Ausbreitung erfolgt durch zueinander senkrecht stehende elektrische und magnetische Felder, die miteinander gekoppelt sind.
In der Physik beschreibt man die Ausbreitung von Wellen durch zwei Arten.
Eine Art von Wellen sind Longitudinalwellen (Längswellen). Datei:Podelna vlna.gif
Die andere Art von Wellen sind Transversalwellen (Querwellen). Datei:Pricna vlna.gif
Bei einer Longitudinalwelle (Längswelle) bewegen sich die schwingungsfähigen Teilchen in Ausbreitungsrichtung.
Beispiel: Schallwellen, Federwelle
Bei einer Transverwalwelle (Querwelle)bewegen sich die schwingungsfähigen Teilchen senkrecht zur Ausbreitungsrichtung.
Beispiel: la-Ola-Welle, Seilwelle, elektromagetische Welle (Licht, Radio, Mikrowelle, ...)
Am Anfang haben wir festgestellt, dass eine Welle eine sich ausbreitende Störung (la-Ola-Welle) oder Schwingung (Schunkeln) ist. Die Geschwindigkeit, mit der sich die Störung bzw. ein Wellenberg (maximale Auslenkung der Schwingung) im Medium ausbreitet, nennt man Ausbreitungsgeschwindigkeit c der Welle. (Beachte, dass hier der Buchstabe c verwendet wird!)
Für die la-Ola-Welle ist die Ausbreitungsgeschwindigkeit die Geschwindigkeit mit der sich die Störung ausbreitet.
Datei:Wave phase.gif Der rote Punkt ist immer am Wellenberg und seine Geschwindigkeit ist die Ausbreitungsgeschwindigkeit der Welle.
Man muss für die Ausbreitungsgeschwindigkeit nicht einen Wellenberg nehmen, sondern es man kann jeden Punkt nehmen, also in dem Bild fixiert man irgendeinen Punkt auf der Sinuslinie und betrachtet dessen Ausbreitung. Da ein Wellenberg ein sehr markanter Punkt ist, hat er hier diese Sonderstellung.
Die Ausbreitungsgeschwindigkeit der Störung wird durch den grünen und roten Punkt dargestellt.
Der grüne Punkt entspricht dem "Wellenberg" der Störung .
Der rote Punkt ist der Beginn der Störung.
Das Diagramm 1 ist ein ty-Diagramm. Über der Zeit t wird der Ort y aufgetragen. Dies ist das Diagramm einer Schwingung.
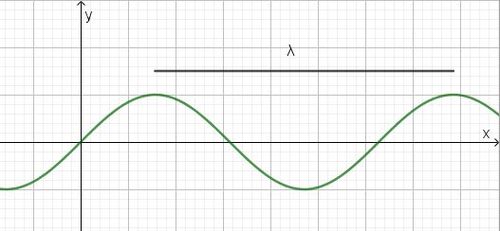
Eine Welle wird durch eine Sinusschwingung angeregt. Es breitet sich dann eine sinusförmige Welle aus. Die Schwingungsdauer der Erregerschwingung ist T, seine Frequenz f. In der Zeit T breitet sich die Welle aus. Der Weg, den ein Wellenberg in der Zeit t zurücklegt ist die Wellenlänge 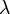 der Welle.
der Welle.
|
Merke:
Die Wellenlänge einer periodischen Welle ist der kleinste Abstand zweier Wellenberg. |
Man kann auch sagen, wenn man einen beliebigen Punkt der Welle nimmt, dass die Wellenlänge der kleinste Abstand zweier Punkte gleicher Phase ist. Dabei bedeutet gleiche Phase, dass der andere Punkt um 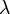 versetzt die gleiche Bewegung wie der ursprüngliche Punkt macht.
versetzt die gleiche Bewegung wie der ursprüngliche Punkt macht.
1. Es ist 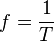 .
.
2. In der Zeit t = T legt der Wellenberg den Weg 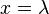 zurück.
zurück.
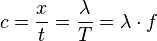 .
.
|
Merke:
Für eine Welle der Wellenlänge |
- 30px Übung
1. Welche Frequenz hat rotes Licht der Wellenlänge 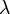 = 700 nm? (1 nm = 10-9m)
= 700 nm? (1 nm = 10-9m)
2. Welche Wellenlänge hat der Kammerton a mit f = 440 Hz?
1. 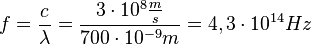
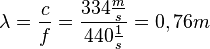
Ein Wassertropfen fällt auf eine Wasseroberfläche und erzeugt eine Welle, die sich kreisförmig ausbreitet.
Diese Wasserwelle wird durch den Wassertropfen erzeugt und breitet sich im Idealfall in konzentrischen Kreisen vom Auftreffpunkt (=Mittelpunkt der konzentrischen Kreise) sinusförmig aus. Jeder Punkt in der Nähe des Auftreffpunktes macht dann nach Anregung eine gedämpfte Sinusschwingung. Zwischen der Erregerschwingung und der Schwinung eines Punktes auf der Wasseroberfläche besteht eine Phasendifferenz. Alle Punkte, die gleichweit vom Erregerzentrum entfernt sind, schwingen in Phase und bilden die Wellenfront.
Wellenfronten einer sich geradlinig ausbreitender Transversalwelle: 300px
Wellenfronten einer Kreiswelle: 200px
Auf den Seiten Seite 1 und Seite 2 von Leifiphysik ist dieses Grundwissen über Wellen nochmals mit schönen Bildern und Animationen zusammengefasst.

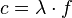 .
.
 gilt:
gilt: 
