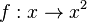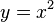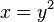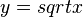Umkehrfunktion Beispiele: Unterschied zwischen den Versionen
Aus RSG-Wiki
| Zeile 1: | Zeile 1: | ||
Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen | Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen | ||
| − | {{Aufgabe|Bestimme die Umkehrfunktion graphisch und | + | {{Aufgabe|Bestimme die Umkehrfunktion graphisch und rechnerisch der Funktion |
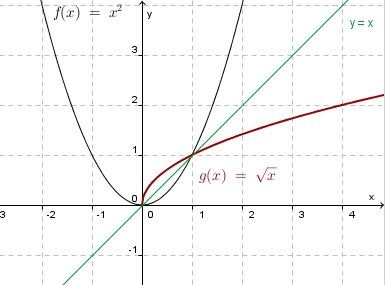
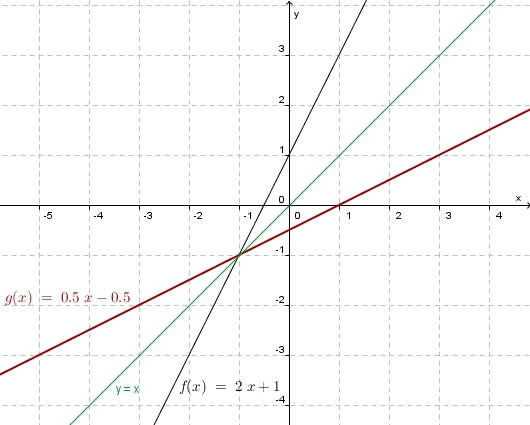
| − | + | 1. <math>f: x \rightarrow 2x + 1</math> | |
| − | + | ||
| + | 2. <math>f: x \rightarrow 1 -0,5x</math> | ||
}} | }} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| + | 1. '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_1.jpg|400]] | ||
| + | |||
| + | '''Rechnerisch: ''' <math> y = 2 x + 1</math><br> | ||
| + | x und y vertauschen: <math>x = 2 y + 1 </math><br> | ||
| + | nach y auflösen: <math>y = \frac{1}{2}x-\frac{1}{2}</math> | ||
| + | |||
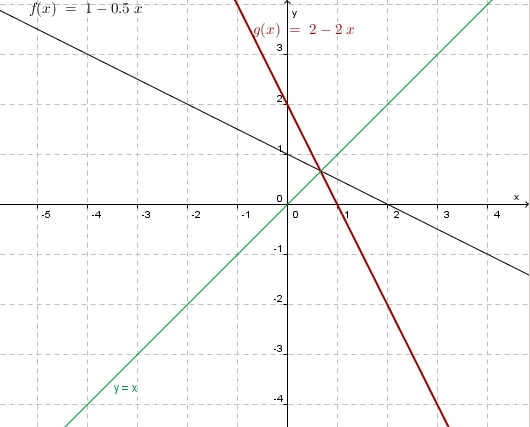
| + | 2. '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_2.jpg|400]] | ||
| + | '''Rechnerisch: ''' <math> y = 1 - 0,5 x</math><br> | ||
| + | x und y vertauschen: <math>x = 1 - 0,5 y </math><br> | ||
| + | nach y auflösen: <math>y = 2 - 2x</math> | ||
}} | }} | ||
| Zeile 18: | Zeile 29: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
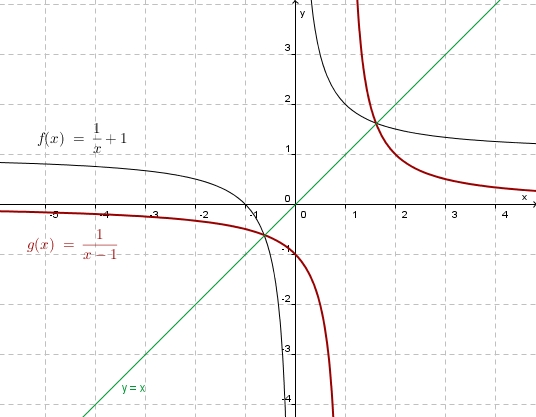
| + | '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_3.jpg|400]] | ||
| + | '''Rechnerisch: ''' <math> y =\frac{1}{x}+1</math><br> | ||
| + | x und y vertauschen: <math>x = \frac{1}{y}+1 </math><br> | ||
| + | nach y auflösen: <math>y = \frac{1}{x-1}</math> | ||
}} | }} | ||
| Zeile 26: | Zeile 41: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| + | '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_4.jpg|400]] | ||
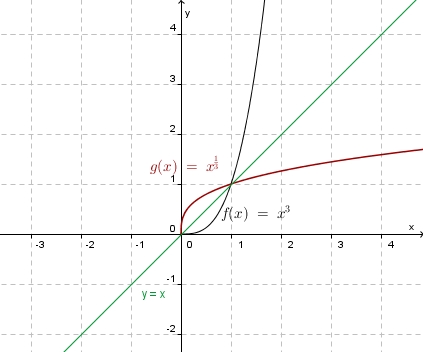
| + | '''Rechnerisch: ''' <math> y =x^3</math><br> | ||
| + | x und y vertauschen: <math>x = y^3 </math><br> | ||
| + | nach y auflösen: <math>y = sqrt[3]{x}</math> | ||
}} | }} | ||
| Zeile 34: | Zeile 53: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| + | '''Graphisch:<br>''' [[Bild:Funktion_umkf_bspl_5.jpg|400]] | ||
| + | '''Rechnerisch: ''' <math> y =x^2</math><br> | ||
| + | x und y vertauschen: <math>x = y^2 </math><br> | ||
| + | nach y auflösen: <math>y = sqrt{x}</math> | ||
}} | }} | ||
Version vom 23. Mai 2012, 06:43 Uhr
Um das bisher behandelte zu üben beginnen wir mit ähnlichen Beispielen, also linearen Funktionen
30px Aufgabe
Bestimme die Umkehrfunktion graphisch und rechnerisch der Funktion 1. 2. |
Rechnerisch: 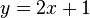
x und y vertauschen: 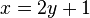
nach y auflösen: 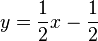
Rechnerisch: 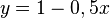
x und y vertauschen: 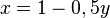
nach y auflösen: 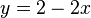
Nun wollen wir auch andere Funktionstypen untersuchen:
30px Aufgabe
Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion
|
30px Aufgabe
Bestimme die Umkehrfunktion durch Wertetabelle, graphisch und algebraisch der Funktion
|
30px Aufgabe
Bestimme die Umkehrfunktion graphisch und algebraisch der Funktion
|
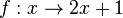
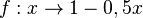
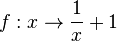
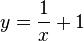
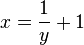
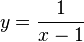
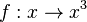
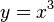
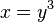
![y = sqrt[3]{x}](/images/math/b/8/d/b8d31f8f5f7f9dca9e5988988e822131.png)