2012-13 Kurs Heim: Unterschied zwischen den Versionen
Berny1 (Diskussion | Beiträge) (→CASIO-Class Pad) |
Berny1 (Diskussion | Beiträge) (→Umkehrfunktion) |
||
| (27 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == | + | == Umkehrfunktion== |
| + | {{#ev:youtube|VdBcocdY2wc|400}}[[Datei:Umkehraufgaben.pdf]] | ||
| + | == Koordinatengeometrie == | ||
| + | * [http://www.zum.de/Faecher/Ek/BAY/gym/mathematik/kollegstufe/glossargeo/RSG%201M1%20Mathematik%20Heim%202009%2010%20%20K%20o%20o%20r%20d%20i%20n%20a%20t%20e%20n%20g%20e%20o%20m%20e%20t%20r%20i%20e%20%20Kursinterne%20Formelsammlung.htm Formelsammlung Koordinatengeometrie] | ||
| + | * Übungsaufgabe Endseer Berg: Skalarprodukt, Vektorprodukt, Anwendungen <br> | ||
| + | :[[Datei:Endseerberg.pdf]] | ||
| + | <br> | ||
| + | {| class="wikitable" | ||
| + | | [[Datei:Kosystem.jpg|600]] ||Stellen wir uns den Weltraum als dreidimensionalen euklidischen Raum vor, auch wenn wir seit Einstein wissen, dass es nicht wirklich so ist.<br><center> {{#ev:youtube|FGcIy76N9sY|200}}</center><br> Dann könnten wir von unserem Sonnensystem mit S(0,0,0) aus allen Fixsternen unserer Galaxie bzw. auch der fremder Galaxien einen räumlichen Punkt mit den Koordinaten (x, y,z) bzw. (x1, x2, x3) zuordnen, wobei x, y und z in Lichtjahren gemessen werden.<br> | ||
| + | <center>{{#ev:youtube|Q46b7yQ6o5o|200}}</center><br> | ||
| + | Wie in "Raumschiff Orion" können wir dann den Weltraum in '''acht Oktanten''' unterteilen. Die direkte Entfernung von zweier Fixsterne kann man dann mittels des Pythagoras bestimmen: | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | {{Definition|1=: | ||
| + | |||
| + | |||
| + | '''Euklidischer Abstand zweier Punkte im RxRxR''' | ||
| + | |||
| + | <math> | ||
| + | d(x,y) = | ||
| + | \sqrt{(x_{1} - y_{1})^2 + (x_{2} - y_{2})^2 + (x_{3} - y_{3})^2} | ||
| + | </math> | ||
| + | }} | ||
| + | |||
| + | {{Aufgabe|1=}} | ||
| + | <popup|Lösung></popup> | ||
| + | '''Vektoren''' | ||
| + | |||
| + | {{Definition|1= '''Anschaulicher Begriff eines Vektors R3:''' | ||
| + | |||
| + | Unter '''einem Vektor''' versteht man die '''Menge aller'''<br> | ||
| + | |||
| + | * gleich gerichteteten und | ||
| + | * gleich orientierten und | ||
| + | * gleich langer | ||
| + | |||
| + | Schiebungspfeile }} | ||
| + | {{#ev:youtube|jzOa-6AU0z4|400}} | ||
| + | |||
| + | {{Merke|1=}} | ||
| + | |||
| + | == {{Schrift grün|Kursthemen}} == | ||
| + | Diese Mindmap zeigt, was wir in Analysis bisher behandelt haben. <br> | ||
| + | [[Datei:Mathemindmap1.jpg|800px]]<br> | ||
| + | Ausnahme: Krümmungsverhalten und Wendepunkte | ||
| + | In Analysis kommt noch das Newtonsche Nullstellenverfahren hinzu! | ||
| + | Ab Mitte Dezember beginnen wir mit Vektorrechnung! | ||
=== Gebrochenrationale Funktionen === | === Gebrochenrationale Funktionen === | ||
| + | |||
| + | Wiederholung rationalen Funktionen: [[rationale Funktionen]] | ||
| + | |||
| + | *[http://www.matheprisma.uni-wuppertal.de/Module/Hyperbel/index.htm Hyperbeln] | ||
| + | *[http://www.brinkmann-du.de/mathe/aufgabenportal/p3_gr_fkt_t_03/p3_gr_fkt_t_03.htm Übungen Polynomdivision] | ||
| + | *[http://www.brinkmann-du.de/mathe/aufgabenportal/p3_gr_fkt_024/p3_gr_fkt_024.htm Übungen Polynomdivision] | ||
| + | |||
| + | [[Asymptoten bei rationalen Funktionen]] | ||
| + | |||
| + | [http://www.netalive.org/rationale-funktionen/chapters/2.3.7.html Symmetrie zum KS] | ||
| + | |||
| + | === Untersuchung von Termen mittels der h-Methode === | ||
| + | {{#ev:youtube|_tbeh8F9G64|400}} | ||
| + | |||
| + | |||
| + | 1. Anwendung: Verhalten an Definitionslücken von gebrochen rationalen Funktionen | ||
| + | |||
| + | 2. Im folgenden Kapitel | ||
| + | |||
=== Differenzen- und Differentialquotient === | === Differenzen- und Differentialquotient === | ||
| − | |||
| + | |||
| + | {{#ev:youtube|wBe6ZiHMfKE|400}} | ||
| + | |||
| + | ==== Anwendungen der Differentialrechnung ==== | ||
| + | |||
| + | ===== Untersuchung von Funktionen auf ihre Eigenschaften ===== | ||
| + | ===== Bestimmung von Funktionen mit bestimmten Eigenschaften! ===== | ||
| + | {{Schrift_grün|'''Aufgabe für die Herbstferien - Vortrag über die Cola-Flasche möglich - melden unter rsg-ws-geo@web.de'''}} | ||
| + | {{Aufgabe| | ||
| + | [[File:GrauburgunderWeinflasche.png|miniatur|100px|handelsübliche Weinflasche - 1 Liter]] | ||
| + | Handelsübliche 1-Liter- Weinflaschen bestehen aus einem zylindrischen Unterteil des Innendurchmessers 8 cm. Der oberste Teil wird durch einen zylindrischen Korken von 2 cm über. Dieser obere nicht zy lindrische Teil geht ist 20 cm hoch.<br> | ||
| + | |||
| + | 1. Welche Bedingung muss eine Funktion erfüllen, die die Flasche als Rotationskörper erzeugen soll?<br> | ||
| + | 2. Bestimmen Sie eine ganzrationale Funkton möglichst niedrigen Grades, die den Rotationskörper (ohne Zylinder erzeugt.<br> | ||
| + | }} | ||
| + | {{Lösung versteckt| | ||
| + | '''1.'''<br> | ||
| + | |||
| + | Bedingungen sind <math> f(0)= 1;f(20)=4 </math> und wegen des horizontalen Überganges zusätzlich | ||
| + | |||
| + | dass die Ableitung an den Stellen 0 und zwanzig 0 ist. | ||
| + | [[Datei: Flasch4.jpg|miniatur||Lösung des Gleichungssystems mit dem Classpad]] | ||
| + | '''2.'''<br> | ||
| + | Für diese 4 Bedingungen muss man mindestens eine ganzrationale Funktion aufstellen. | ||
| + | |||
| + | <math>y =ax^3 + bx^2 + cx +d </math> mit der Ableitung | ||
| + | <math>y =3ax^2 + 2bx + c </math><br> | ||
| + | Also ergibt sich das Gleichungssystem<br> | ||
| + | |||
| + | (1)<math>1 = d </math><br> | ||
| + | (2)<math>0 = c </math><br> | ||
| + | (3)<math>4 = 8000 a + 400 b + 20 c + d </math><br> | ||
| + | (4)<math>0 = 1200 a + 40 b + c</math><br>, | ||
| + | <br> | ||
| + | welches durch (1) und (2) auf zwei Gleichungen mit zwei Unbekannten reduziert wird und die | ||
| + | Lösungen | ||
| + | |||
| + | (1)<math>a=-3/4000, b = 9/400, c=0 </math> und <math> d = 1 </math>besitzt.<br> | ||
| + | |||
| + | '''Ergänzung'''<br> | ||
| + | [[Datei:Visflasche1.JPG]] | ||
| + | |||
| + | |||
| + | |||
| + | }} | ||
| + | <br> | ||
| + | |||
| + | Für weitere Untersuchungen: | ||
| + | |||
| + | [[File:Double Cola.jpg|100px]] | ||
| + | {{Aufgabe| | ||
| + | Entnehmen Sie ausgehend von der Höhe von 20 cm der abgebildeten Flasche wesentliche Werte für eine mathematische Modellierung der Flasche. Welchen Grad muss eine ganzrationale Funktion besitzen, um die Flasche als Rotationskörper im Intervall von 0 bis 20] zu erzeugen? Bestimmen Sie diese Funktion.<br> Bestimmen Sie für einen Glasballon, den Sie zuhause besitzen eine erzeugende Funktion und stellen Sie den Glasballon mit dem Ergebnis in einer Präsentation vor. }} | ||
| + | [[File:Glasballon.JPG||400px]] | ||
| + | |||
| + | == {{Schrift grün|Grundwissen }} == | ||
| + | === Sinus- und Kosinusfunktion - Einfluss von Parametern auf den Graphen Jg 10=== | ||
| + | |||
| + | [[File:Freizeitbad Sylter Welle Westerland auf Sylt 2012 PD 1.JPG|miniatur|300px|Überlege den Zusammenhang mit der Sinusfunktion]] | ||
| + | [[Bild: e-learn.gif]][http://www.geogebratube.org/student/m18424 Die Sinusfunktion am Einheitskreis]<br> | ||
| + | [[Bild: e-learn.gif]][http://www.geogebratube.org/student/m18425 Die allgemeine Sinusfunktion mit Parametern] | ||
| + | |||
| + | [[Bild: e-learn.gif]][http://wikis.zum.de/medienvielfalt/Trigonometrische_Funktionen Lernpfad Trigonometrische Funktionen] | ||
| + | |||
| + | [[Bild:Aktuell.jpg]] | ||
| + | === Quadratische Gleichungen - Lösungsstrategien (Jg. 9)=== | ||
| + | |||
| + | <center> | ||
| + | [[Datei:Qgl.gif]] | ||
| + | <br> | ||
| + | |||
| + | Hier kannst Du die Präsentation im Unterricht als PDF herunterladen: <br><br>[[Datei:QuadratischeGleichungen.pdf]] </center> | ||
| + | |||
| + | *[[Datei:e-learn.gif]][http://wiki.zum.de/Quadratische_Funktion Alles zu quadratischen Funktionen] | ||
| + | *[http://www.arndt-bruenner.de/mathe/java/gleichungenloesen.htm#gleichungen Interaktive Übungen - Stufe 2] | ||
| + | |||
| + | [[Bild:Aktuell.jpg]]Variation von Funktionen<br> | ||
| + | <ggb_applet height="600" width="800" | ||
| + | filename="VariationFunktion.ggb" /><br> | ||
| + | {{Aufgabe|1. | ||
| + | <br> Verändere jeweils ausgehend von <math> a = 1,b=0 ,c = 1 , d= 0 </math> die einzelnen Parameter und beschreibe den Einfluss der Veränderung <br> | ||
| + | 2. <br>Ersetze die Funktion g durch <math> g(x) = sin(x)und f durch f(x) a*sin(c*x -b)+ d.</math> Erinnere Dich an die 10. Klasse! Wiederhole die Aufgabe 1 mit den neuen Funktionen. }} | ||
| + | {{Lösung versteckt}} | ||
| + | === Allgemein === | ||
| + | '''Generell zum wiederholenden Üben :''' | ||
| + | |||
| + | [[Bild: Ueben.gif]][[Grundlegende Kenntnisse in Mathematik]] | ||
| + | Grundwissenskataloge: [http://www.rhoen-gymnasium.de/mathe/ Grundwissenskatalog des Rhöngymnasiums]'''am RSG verpflichtend eingeführt''' | ||
| + | |||
| + | |||
| + | |||
| + | <table cellpadding="0" cellspacing="0" border="1" | ||
| + | style="text-align: left; width: 100%; background-color: rgb(153, 255, 153);"> | ||
| + | <tr style="color: rgb(153, 51, 0);"> | ||
| + | <td style="vertical-align: top; background-color: rgb(153, 255, 153); text-align: center;"> | ||
| + | |||
| + | |||
| + | ===Wiederholung wichtiger Grundfunktionen === | ||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);"> | ||
| + | |||
| + | Diese Zusammenfassung sollst Du Dir ausdrucken: | ||
| + | |||
| + | |||
| + | *[http://www.gymnasium-stein.de/filedownload/Fachschaften/Faecher_Gruppe_2/Mathematik/Downloads/Wichtige_Funktionstypen.pdf Übersicht über Funktionen (zum Ausdruck, vom Gymnasium Stein)] | ||
| + | |||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);"> | ||
| + | |||
| + | |||
| + | '''Lineare Funktionen''' <br> | ||
| + | |||
| + | [[Bild:lernpfad.jpg]] | ||
| + | *[http://www.matheprisma.de/Module/Geraden/index.htm Geradengleichungen] | ||
| + | *[[Wiederholung lineare Funktionen]] | ||
| + | *Viele ... viele ... Übungen auf der Seinte von [http://www.realmath.de/Mathematik/newmath8.htm realmath.de] | ||
| + | |||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);"> | ||
| + | |||
| + | '''Quadratische Funktionen''' <br> | ||
| + | |||
| + | |||
| + | |||
| + | [[bild:e-learn.gif]][http://wikis.zum.de/medienvielfalt/index.php/Einf%C3%BChrung_in_quadratische_Funktionen Lernpfad zu quadratischen Funktionen] | ||
| + | |||
| + | '''Parabelgleichungen aufstellen - zuordnen''' | ||
| + | |||
| + | [[Bild:e-learn.gif]][[Bild:ueben.gif]] | ||
| + | *[http://www.zum.de/dwu/umamfu2.htm Lerneinheiten zu Parabeln] (e-Learning) | ||
| + | *[http://brinkmann-du.de/mathe/rbtest/2puzzle/fkt_erkennen_001.htm Lineare und quadratische Funktionen] (interaktiv) | ||
| + | |||
| + | '''Scheitel bestimmen''' | ||
| + | |||
| + | *[http://www.arndt-bruenner.de/mathe/10/scheitelpunkt.htm Scheitel bestimmen - mit Umformungen an beliebiegen quadr. Funktionen] | ||
| + | *[http://www.realmath.de/Neues/Klasse9/parabueb/parabelscheitel.html Interaktive Übung zur Scheitelbestimmung] | ||
| + | |||
| + | '''Anwendungen''' | ||
| + | |||
| + | '''Extremwertaufgaben''' | ||
| + | |||
| + | [[Bild: Ueben.gif]] | ||
| + | *[http://www.physik-im-unterricht.de/emg/G8_Mathe_Klasse_9/M9-Extremwertaufgaben.pdf Extremwertaufgaben zu Parabeln] - mit Lösungen | ||
| + | |||
| + | *eine [http://www.physik-im-unterricht.de/emg/G8_Mathe_Klasse_9/M9-Ex2-03-2008.pdf Stegreifaufgabe zu Extremwerten und Tangenten] an Parabeln mit Lösungen | ||
| + | |||
| + | '''Tangenten an Parabeln''' | ||
| + | |||
| + | *[http://wiki.zum.de/Ber%C3%BChrungsprobleme_bei_quadratischen_Funktionen Sich berührende Graphen] | ||
| + | |||
| + | * [http://www.realmath.de/Neues/Klasse9/tangenten/Tangente.html Tangentengleichung an Parabel bestimmen für ein Geradenbüschel] | ||
| + | |||
| + | *[http://www.dynama.de/dynageo/9/extremwert2/extremwert2.html Graphische Veranschaulichung] (DYNAGEO) | ||
| + | |||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);"> | ||
| + | |||
| + | '''Funktionen des Typs a/(x+b) + c (Hyperbeln)'''<br> | ||
| + | |||
| + | *[http://www.matheprisma.uni-wuppertal.de/Module/Hyperbel/index.htm Hyperbeln und rationale Funktionen] | ||
| + | *[[Bild:lernpfad.jpg]] [[rationale Funktionen]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);"> | ||
| + | |||
| + | '''Potenzfunktionen'''<br> | ||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);"> | ||
| + | |||
| + | '''Exponentialfunktionen'''<br> | ||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td style="vertical-align: top; height: 2px; background-color: rgb(255, 255, 204);"> | ||
| + | |||
| + | '''Sinus- und Kosinusfunktion''' <br> | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | |||
| + | == {{Schrift grün|Informationen }} == | ||
| + | |||
| + | ===Merkhilfe=== | ||
| + | Die aktualisierte Fassung der Merkhilfe steht auf den Seiten des ISB unter [http://www.isb.bayern.de/isb/index.asp?MNav=6&QNav=12&TNav=1&INav=0&Pub=995] zum Download bereit. | ||
===Länderübergreifendes Abitur === | ===Länderübergreifendes Abitur === | ||
[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=22e5bb1a3fd9068cbeb4e5135aa4103a Musteraufgabe mit Zusatzinformationen] | [http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=22e5bb1a3fd9068cbeb4e5135aa4103a Musteraufgabe mit Zusatzinformationen] | ||
| Zeile 19: | Zeile 281: | ||
*[http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek2/cas/classpad/ Arbeitsblätter] | *[http://www.schule-bw.de/unterricht/faecher/mathematik/3material/sek2/cas/classpad/ Arbeitsblätter] | ||
*[http://www.casio-europe.com/de/drucken/calc/sgr/produkte/zubehoer/rmclasspadset/arbeitsblaetter/ Abeitsblätter von CASIO] | *[http://www.casio-europe.com/de/drucken/calc/sgr/produkte/zubehoer/rmclasspadset/arbeitsblaetter/ Abeitsblätter von CASIO] | ||
| + | |||
| + | {{Schrift_grün|Kostenlose Software zum Download CASIO Classpad 330 90-Tage Testversion}} | ||
| + | [http://www.casio-schulrechner.de/de/produkte/zubehoer/classpadmanager30/managerdemo/ Download] | ||
Aktuelle Version vom 11. März 2013, 12:57 Uhr
Inhaltsverzeichnis |
Umkehrfunktion

Koordinatengeometrie
- Formelsammlung Koordinatengeometrie
- Übungsaufgabe Endseer Berg: Skalarprodukt, Vektorprodukt, Anwendungen
Definition
Euklidischer Abstand zweier Punkte im RxRxR
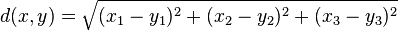
30px Aufgabe
|
<popup|Lösung></popup> Vektoren
Definition
Anschaulicher Begriff eines Vektors R3:
Unter einem Vektor versteht man die Menge aller
- gleich gerichteteten und
- gleich orientierten und
- gleich langer
Schiebungspfeile
30px Merke
|
Kursthemen
Diese Mindmap zeigt, was wir in Analysis bisher behandelt haben.
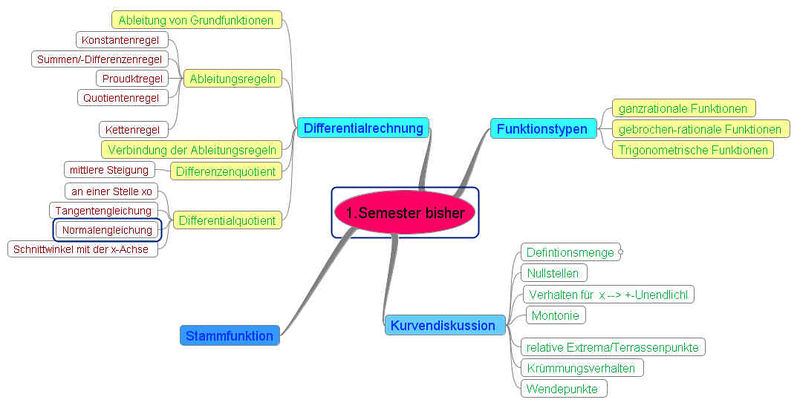
Ausnahme: Krümmungsverhalten und Wendepunkte
In Analysis kommt noch das Newtonsche Nullstellenverfahren hinzu!
Ab Mitte Dezember beginnen wir mit Vektorrechnung!
Gebrochenrationale Funktionen
Wiederholung rationalen Funktionen: rationale Funktionen
Asymptoten bei rationalen Funktionen
Untersuchung von Termen mittels der h-Methode
1. Anwendung: Verhalten an Definitionslücken von gebrochen rationalen Funktionen
2. Im folgenden Kapitel
Differenzen- und Differentialquotient
Anwendungen der Differentialrechnung
Untersuchung von Funktionen auf ihre Eigenschaften
Bestimmung von Funktionen mit bestimmten Eigenschaften!
Aufgabe für die Herbstferien - Vortrag über die Cola-Flasche möglich - melden unter rsg-ws-geo@web.de
30px Aufgabe
Datei:GrauburgunderWeinflasche.png handelsübliche Weinflasche - 1 Liter Handelsübliche 1-Liter- Weinflaschen bestehen aus einem zylindrischen Unterteil des Innendurchmessers 8 cm. Der oberste Teil wird durch einen zylindrischen Korken von 2 cm über. Dieser obere nicht zy lindrische Teil geht ist 20 cm hoch. 1. Welche Bedingung muss eine Funktion erfüllen, die die Flasche als Rotationskörper erzeugen soll? |
1.
Bedingungen sind 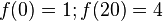 und wegen des horizontalen Überganges zusätzlich
und wegen des horizontalen Überganges zusätzlich
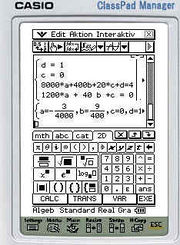
dass die Ableitung an den Stellen 0 und zwanzig 0 ist.
2.
Für diese 4 Bedingungen muss man mindestens eine ganzrationale Funktion aufstellen.
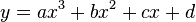 mit der Ableitung
mit der Ableitung
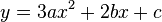
Also ergibt sich das Gleichungssystem
(1)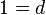
(2)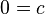
(3)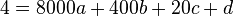
(4)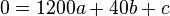
,
welches durch (1) und (2) auf zwei Gleichungen mit zwei Unbekannten reduziert wird und die
Lösungen
(1)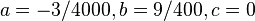 und
und 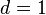 besitzt.
besitzt.
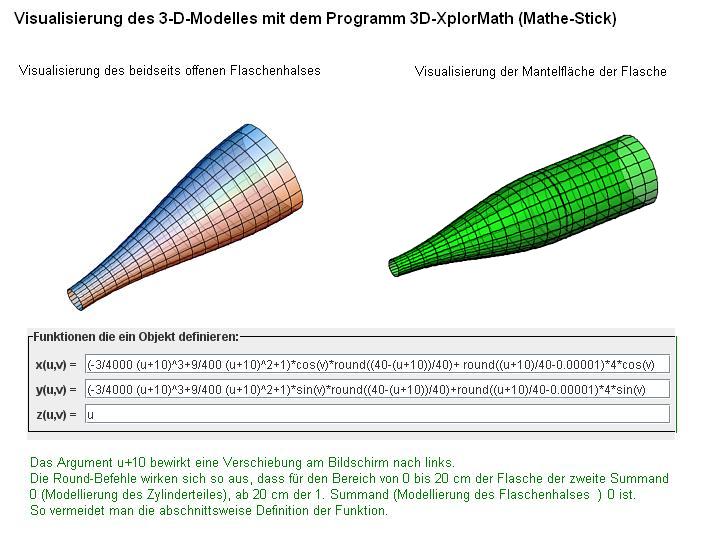
Für weitere Untersuchungen:
30px Aufgabe
Entnehmen Sie ausgehend von der Höhe von 20 cm der abgebildeten Flasche wesentliche Werte für eine mathematische Modellierung der Flasche. Welchen Grad muss eine ganzrationale Funktion besitzen, um die Flasche als Rotationskörper im Intervall von 0 bis 20] zu erzeugen? Bestimmen Sie diese Funktion. |
Grundwissen
Sinus- und Kosinusfunktion - Einfluss von Parametern auf den Graphen Jg 10
![]() Die Sinusfunktion am Einheitskreis
Die Sinusfunktion am Einheitskreis
![]() Die allgemeine Sinusfunktion mit Parametern
Die allgemeine Sinusfunktion mit Parametern
![]() Lernpfad Trigonometrische Funktionen
Lernpfad Trigonometrische Funktionen
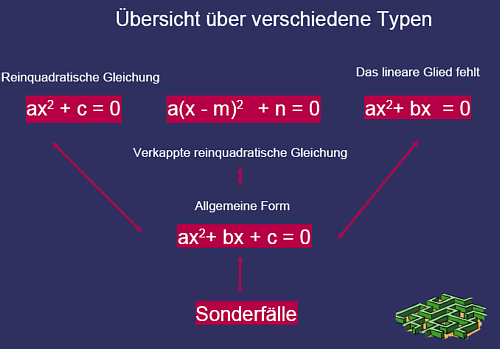
Quadratische Gleichungen - Lösungsstrategien (Jg. 9)

30px Aufgabe
1.
|
Allgemein
Generell zum wiederholenden Üben :
![]() Grundlegende Kenntnisse in Mathematik
Grundwissenskataloge: Grundwissenskatalog des Rhöngymnasiumsam RSG verpflichtend eingeführt
Grundlegende Kenntnisse in Mathematik
Grundwissenskataloge: Grundwissenskatalog des Rhöngymnasiumsam RSG verpflichtend eingeführt
|
Wiederholung wichtiger Grundfunktionen |
|
Diese Zusammenfassung sollst Du Dir ausdrucken:
|
|
|
|
Quadratische Funktionen
Parabelgleichungen aufstellen - zuordnen
Scheitel bestimmen
Anwendungen Extremwertaufgaben
Tangenten an Parabeln
|
|
Funktionen des Typs a/(x+b) + c (Hyperbeln) |
|
Potenzfunktionen |
|
Exponentialfunktionen |
|
Sinus- und Kosinusfunktion |
Informationen
Merkhilfe
Die aktualisierte Fassung der Merkhilfe steht auf den Seiten des ISB unter [1] zum Download bereit.
Länderübergreifendes Abitur
Musteraufgabe mit Zusatzinformationen
CAS-Abitur - traditionelles Abitur
Matheabi
unterscheidet sich nur in Geringfügigkeiten vom
CAS-Matheabi
CASIO-Class Pad
Die pdf-Datei kann im Adobe-Reader nach Stichworten durchsucht werden. Also nicht vor der Seitenzahl erschrecken°
- Der Class-Pad im Matheabi von Niedersachsen
- Anwendungsbeispiele
- Arbeitsblätter
- Abeitsblätter von CASIO
Kostenlose Software zum Download CASIO Classpad 330 90-Tage Testversion Download

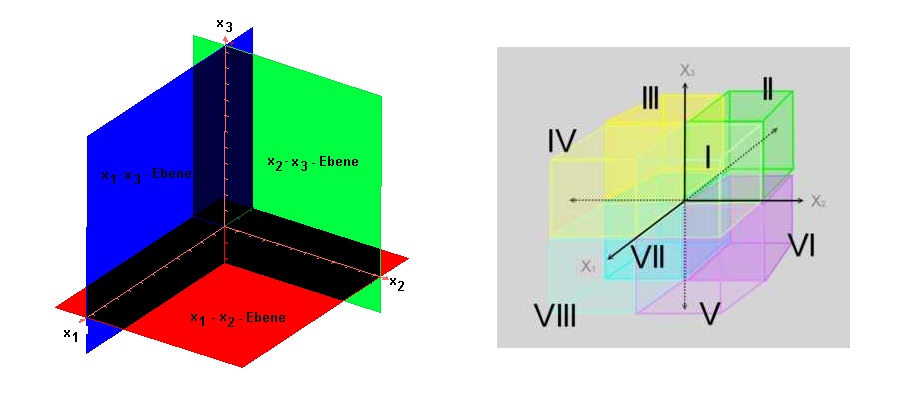
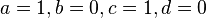 die einzelnen Parameter und beschreibe den Einfluss der Veränderung
die einzelnen Parameter und beschreibe den Einfluss der Veränderung 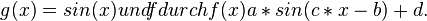 Erinnere Dich an die 10. Klasse! Wiederhole die Aufgabe 1 mit den neuen Funktionen.
Erinnere Dich an die 10. Klasse! Wiederhole die Aufgabe 1 mit den neuen Funktionen.

