2012-13 Kurs Heim
Inhaltsverzeichnis |
Umkehrfunktion

Koordinatengeometrie
- Formelsammlung Koordinatengeometrie
- Übungsaufgabe Endseer Berg: Skalarprodukt, Vektorprodukt, Anwendungen
Definition
Euklidischer Abstand zweier Punkte im RxRxR
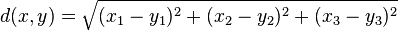
30px Aufgabe
|
<popup|Lösung></popup> Vektoren
Definition
Anschaulicher Begriff eines Vektors R3:
Unter einem Vektor versteht man die Menge aller
- gleich gerichteteten und
- gleich orientierten und
- gleich langer
Schiebungspfeile
30px Merke
|
Kursthemen
Diese Mindmap zeigt, was wir in Analysis bisher behandelt haben.
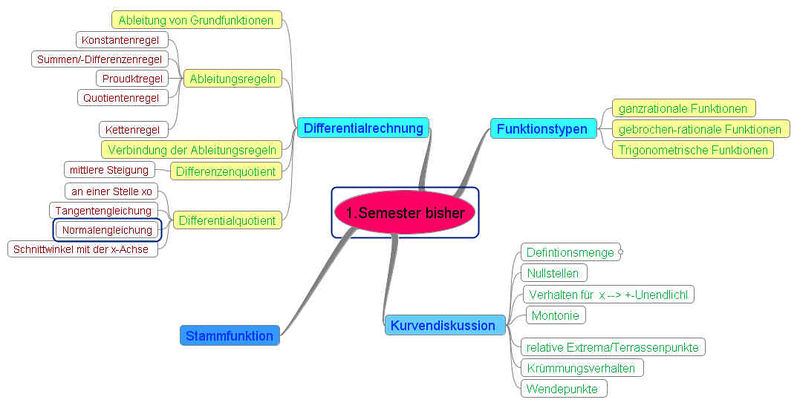
Ausnahme: Krümmungsverhalten und Wendepunkte
In Analysis kommt noch das Newtonsche Nullstellenverfahren hinzu!
Ab Mitte Dezember beginnen wir mit Vektorrechnung!
Gebrochenrationale Funktionen
Wiederholung rationalen Funktionen: rationale Funktionen
Asymptoten bei rationalen Funktionen
Untersuchung von Termen mittels der h-Methode
1. Anwendung: Verhalten an Definitionslücken von gebrochen rationalen Funktionen
2. Im folgenden Kapitel
Differenzen- und Differentialquotient
Anwendungen der Differentialrechnung
Untersuchung von Funktionen auf ihre Eigenschaften
Bestimmung von Funktionen mit bestimmten Eigenschaften!
Aufgabe für die Herbstferien - Vortrag über die Cola-Flasche möglich - melden unter rsg-ws-geo@web.de
30px Aufgabe
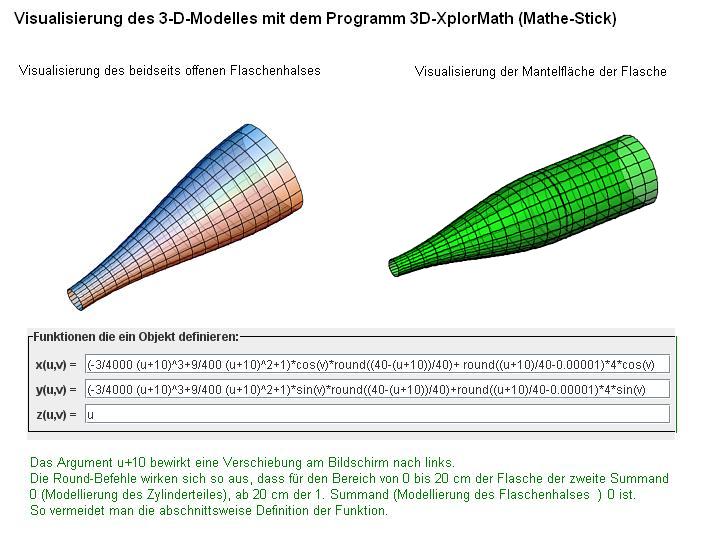
Datei:GrauburgunderWeinflasche.png handelsübliche Weinflasche - 1 Liter Handelsübliche 1-Liter- Weinflaschen bestehen aus einem zylindrischen Unterteil des Innendurchmessers 8 cm. Der oberste Teil wird durch einen zylindrischen Korken von 2 cm über. Dieser obere nicht zy lindrische Teil geht ist 20 cm hoch. 1. Welche Bedingung muss eine Funktion erfüllen, die die Flasche als Rotationskörper erzeugen soll? |
1.
Bedingungen sind 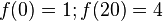 und wegen des horizontalen Überganges zusätzlich
und wegen des horizontalen Überganges zusätzlich
dass die Ableitung an den Stellen 0 und zwanzig 0 ist.
2.
Für diese 4 Bedingungen muss man mindestens eine ganzrationale Funktion aufstellen.
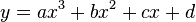 mit der Ableitung
mit der Ableitung
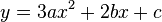
Also ergibt sich das Gleichungssystem
(1)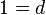
(2)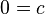
(3)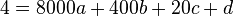
(4)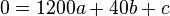
,
welches durch (1) und (2) auf zwei Gleichungen mit zwei Unbekannten reduziert wird und die
Lösungen
(1)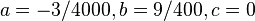 und
und 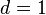 besitzt.
besitzt.
Für weitere Untersuchungen:
30px Aufgabe
Entnehmen Sie ausgehend von der Höhe von 20 cm der abgebildeten Flasche wesentliche Werte für eine mathematische Modellierung der Flasche. Welchen Grad muss eine ganzrationale Funktion besitzen, um die Flasche als Rotationskörper im Intervall von 0 bis 20] zu erzeugen? Bestimmen Sie diese Funktion. |
Grundwissen
Sinus- und Kosinusfunktion - Einfluss von Parametern auf den Graphen Jg 10
![]() Die Sinusfunktion am Einheitskreis
Die Sinusfunktion am Einheitskreis
![]() Die allgemeine Sinusfunktion mit Parametern
Die allgemeine Sinusfunktion mit Parametern
![]() Lernpfad Trigonometrische Funktionen
Lernpfad Trigonometrische Funktionen
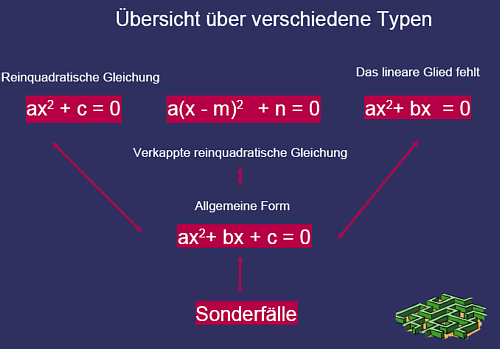
Quadratische Gleichungen - Lösungsstrategien (Jg. 9)

30px Aufgabe
1.
|
Allgemein
Generell zum wiederholenden Üben :
![]() Grundlegende Kenntnisse in Mathematik
Grundwissenskataloge: Grundwissenskatalog des Rhöngymnasiumsam RSG verpflichtend eingeführt
Grundlegende Kenntnisse in Mathematik
Grundwissenskataloge: Grundwissenskatalog des Rhöngymnasiumsam RSG verpflichtend eingeführt
|
Wiederholung wichtiger Grundfunktionen |
|
Diese Zusammenfassung sollst Du Dir ausdrucken:
|
|
|
|
Quadratische Funktionen
Parabelgleichungen aufstellen - zuordnen
Scheitel bestimmen
Anwendungen Extremwertaufgaben
Tangenten an Parabeln
|
|
Funktionen des Typs a/(x+b) + c (Hyperbeln) |
|
Potenzfunktionen |
|
Exponentialfunktionen |
|
Sinus- und Kosinusfunktion |
Informationen
Merkhilfe
Die aktualisierte Fassung der Merkhilfe steht auf den Seiten des ISB unter [1] zum Download bereit.
Länderübergreifendes Abitur
Musteraufgabe mit Zusatzinformationen
CAS-Abitur - traditionelles Abitur
Matheabi
unterscheidet sich nur in Geringfügigkeiten vom
CAS-Matheabi
CASIO-Class Pad
Die pdf-Datei kann im Adobe-Reader nach Stichworten durchsucht werden. Also nicht vor der Seitenzahl erschrecken°
- Der Class-Pad im Matheabi von Niedersachsen
- Anwendungsbeispiele
- Arbeitsblätter
- Abeitsblätter von CASIO
Kostenlose Software zum Download CASIO Classpad 330 90-Tage Testversion Download

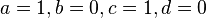 die einzelnen Parameter und beschreibe den Einfluss der Veränderung
die einzelnen Parameter und beschreibe den Einfluss der Veränderung 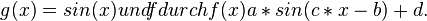 Erinnere Dich an die 10. Klasse! Wiederhole die Aufgabe 1 mit den neuen Funktionen.
Erinnere Dich an die 10. Klasse! Wiederhole die Aufgabe 1 mit den neuen Funktionen.

