Kreise und Tangenten: Unterschied zwischen den Versionen
Aus RSG-Wiki
Berny1 (Diskussion | Beiträge) (→{{Schrift_grün|Ein Nachtrag zur Sofi am 20. März 2015}}) |
Berny1 (Diskussion | Beiträge) (→{{Schrift_grün|Eine Konstruktion von Tangenten an zwei Kreise}}) |
||
| Zeile 33: | Zeile 33: | ||
= {{Schrift_grün|Eine Konstruktion von Tangenten an zwei Kreise}} = | = {{Schrift_grün|Eine Konstruktion von Tangenten an zwei Kreise}} = | ||
{{Aufgaben-blau|1=|2= | {{Aufgaben-blau|1=|2= | ||
| + | |||
| + | An zwei Kreise mit z.B. r1 = 3 cm und r2 = 5 cm, die sich nicht schneiden sollen gemeinsame Tangenten konstruiert werden. | ||
| + | |||
| + | {{Schrift_grün|'''Hilfe''':<br> | ||
| + | * Konstruiere zwei Hilfskreise mit der Summe bzw. der Differenz der beiden Radien um den Mittelpunkt des Kreises mit dem größeren Radius. | ||
| + | * Konstruiere dann die Tangenten vom Mittelpunkt des kleineren Kreises an die beiden Hilfskreise- | ||
| + | }} | ||
| + | |||
| + | * Überlege nun, wie man aus diesen Tangenten die gemeinsamen Tangenten an die beiden gegebenen Kreise erhält! | ||
| + | <br> | ||
| + | |||
| + | '''Hier kannst Du mit Geogebra konstruieren!''' | ||
| + | |||
<iframe scrolling="no" src="https://tube.geogebra.org/material/iframe/id/882793/width/1366/height/631/border/888888/rc/true/ai/true/sdz/true/smb/true/stb/true/stbh/true/ld/true/sri/true/at/auto" width="1366px" height="631px" style="border:0px;"> </iframe> | <iframe scrolling="no" src="https://tube.geogebra.org/material/iframe/id/882793/width/1366/height/631/border/888888/rc/true/ai/true/sdz/true/smb/true/stb/true/stbh/true/ld/true/sri/true/at/auto" width="1366px" height="631px" style="border:0px;"> </iframe> | ||
}}<br>br | }}<br>br | ||
Version vom 23. März 2015, 19:53 Uhr
Inhaltsverzeichnis[Verbergen] |
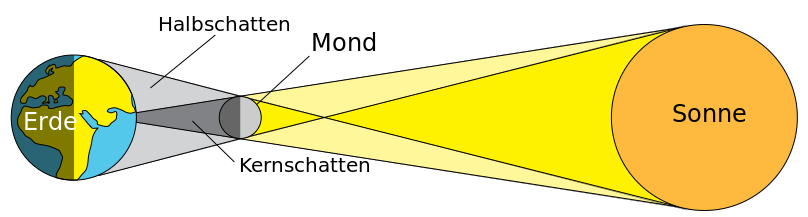
Ein Nachtrag zur Sofi am 20. März 2015
Sekante - Tangente - Passante
|
Merke:
|
Konstruktion von Tangenten von einem Punkt an einen Kreis
|
Merke:
|
Eine Konstruktion von Tangenten an zwei Kreise
br