Bruchterme und Bruchgleichungen: Unterschied zwischen den Versionen

Aus RSG-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Hinweis: Der Link öffnet sich in einem eigenen Fenster, wenn du beim Anklicken mit der Maus die Shift-Taste drückst. *Eine ausführliche Erklärung zu Brucht…“)
 
 
(7 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
Hinweis:  
 
Hinweis:  
−
  Der Link öffnet sich in einem eigenen Fenster, wenn du beim Anklicken mit der Maus die Shift-Taste drückst.
+
  Der Link öffnet sich in einem eigenen Fenster, wenn du beim Anklicken mit der Maus <br>
 +
die Shift-Taste drückst.
  
−
*Eine ausführliche Erklärung zu Bruchtermen und Bruchgleichungen mit Umformungen und Rechenbeispielen findest du [http://www.arndt-bruenner.de/mathe/9/bruchtermeundgleichungen.htm auf dieser Seite]
 
  
−
*Zum Kürzen von Bruchtermen findest du Übungsmaterial [http://www.mathe-trainer.de/Klasse8/Termumformungen/Bruchterme/Block1/Aufgaben.htm auf dieser Seite]
+
=Bruchterme=
 +
 
 +
* Auf dieser [http://de.bettermarks.com/mathe-portal/mathebuch/rechnen-mit-bruchtermen.html Seite] wird erklärt wie man Bruchterme kürzt, erweitert, Bruchterme addiert, subtrahiert, multipliziert und dividiert.
 +
 
 +
* Beachte, dass Terme wie <math>x-1</math> und <math> 1-x</math> sehr ähnlich sind und du kannst den einen Term durch Ausklammern von <math>-1</math> in den anderen überführen: <math> 1-x=-(-1+x)=-(x-1)</math>.<br>
 +
Das Minuszeichen vom Nenner kannst du auch vor den Bruch schreiben! <math>\frac{1}{1-x}= \frac{1}{-(x-1)} = - \frac{1}{x-1}</math><br>
 +
Dann ist <math> \frac{1}{x-1}+\frac{1}{1-x}=\frac{1}{x-1}+\frac{1}{-(-1+x)}=\frac{1}{x-1}+\frac{-1}{x-1}=\frac{1}{x-1}-\frac{1}{x-1}=0</math><br>
 +
 
 +
* Beachte außerdem, dass du nie aus Summen kürzen darfst!<br>
 +
Beispiel 1:<math> \frac{1+x}{2+x} \not= \frac{1}{2}</math> , Beispiel 2: <math> \frac{1+x^2}{2+x} \not= \frac{1+x}{2}</math>, Beispiel 3: <math> \frac{x^2-4}{x-4} \not= \frac{x-4}{4}</math>  <span style="color:red;">x darf man <u>nicht</u> kürzen!</span><br>
 +
Beispiel 4: <math> \frac{x^2-4}{x-4} \not= \frac{x^2}{x}</math>, Beispiel 5: <math> \frac{x-4a}{x-4b} \not= \frac{x-a}{x-b}</math> <span style="color:red;">4 darf man <u>nicht</u> kürzen!</span>
 +
 
 +
 
 +
[[Datei: video2.jpg]] [https://www.youtube.com/watch?v=LFwOeu_RA-4 Kürzen und Erweitern], [https://www.youtube.com/watch?v=-546Pg3rDCA Bruchterme],<br>
 +
von TheSimpleMaths: [https://www.youtube.com/watch?v=2Ib7Tqhd2lc Bruchterme vereinfachen], [https://www.youtube.com/watch?v=dcybZtakrEQ Grundlagen], [https://www.youtube.com/watch?v=azSzsyTX80k Tipps und Tricks]
 +
 
 +
'''Aufgaben:''' <br>
 
Du brauchst Stift und Papier und rechnest selbst. Wenn du fertig bist, kannst du deine Lösung vergleichen.
 
Du brauchst Stift und Papier und rechnest selbst. Wenn du fertig bist, kannst du deine Lösung vergleichen.
  
−
*Das Addieren von Brüchen übst du [http://www.mathe-trainer.de/Klasse8/Termumformungen/Bruchterme/Block3/Aufgaben.htm beim Mathe-Trainer mit Lösungen].Dabei rechnest du mit Stift und Papier und vergleichst anschließend deine Lösung.
+
[http://www.mathe-trainer.de/Klasse8/Termumformungen/Bruchterme/Block1/Aufgaben.htm#Ziel Kürzen]<br>
 +
[http://www.mathe-trainer.de/Klasse8/Termumformungen/Bruchterme/Block3/Aufgaben.htm Addition]<br>
 +
[http://www.mathe-trainer.de/Klasse8/Termumformungen/Bruchterme/Block2/Aufgaben.htm Multiplikation]
 +
 
 +
[[Binomische_Formeln]] - Binomische Formeln sind oft hilfreich beim Rechnen mit Bruchtermen.
 +
 
 +
=Bruchgleichungen=
 +
 
 +
*Eine ausführliche Erklärung zu Bruchtermen und Bruchgleichungen mit Umformungen und Rechenbeispielen findest du [http://www.arndt-bruenner.de/mathe/9/bruchtermeundgleichungen.htm auf dieser Seite]
 +
 
 +
[http://www.mathebibel.de/bruchgleichungen-loesen So löst man Bruchgleichungen]
 +
 
 +
[[Datei: video2.jpg]] [https://www.youtube.com/watch?v=x58zKQ5pf2E Bruchgleichungen von TheSimpleMaths], [https://www.youtube.com/watch?v=4JegreHK2z4 Beispiel], [https://www.youtube.com/watch?v=SQI2gcatrso Bruchgleichungen], [https://www.youtube.com/watch?v=n2KpJeTc5dc schwierigere Aufgabe]
  
−
*Das Multiplizieren von Bruchtermen übst du [http://www.mathe-trainer.de/Klasse8/Termumformungen/Bruchterme/Block2/Aufgaben.htm auf dieser Seite].Selbst rechnen und dann Lösung vergleichen.
+
Aufgaben: <br>
 +
[http://www.brinkmann-du.de/mathe/aufgabenportal/p0_bruchgl_01/p0_bruchgl_01.htm Aufgaben mit Lösungen] - Bearbeite die Aufgaben 1 und 2!<br>
 +
[http://www.raschweb.de/M8-Bruchgleichung-Aufgaben.pdf weitere Aufgaben mit Lösungen]

Aktuelle Version vom 1. Juni 2016, 08:00 Uhr

Hinweis: 

Der Link öffnet sich in einem eigenen Fenster, wenn du beim Anklicken mit der Maus 

die Shift-Taste drückst.


Bruchterme

  • Auf dieser Seite wird erklärt wie man Bruchterme kürzt, erweitert, Bruchterme addiert, subtrahiert, multipliziert und dividiert.
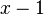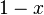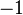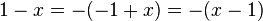  • Beachte, dass Terme wie x-1 und 1-x sehr ähnlich sind und du kannst den einen Term durch Ausklammern von -1 in den anderen überführen: 1-x=-(-1+x)=-(x-1).

Das Minuszeichen vom Nenner kannst du auch vor den Bruch schreiben! 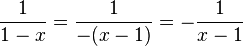\frac{1}{1-x}= \frac{1}{-(x-1)} = - \frac{1}{x-1}
Dann ist 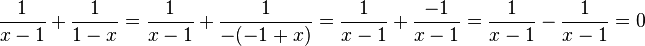\frac{1}{x-1}+\frac{1}{1-x}=\frac{1}{x-1}+\frac{1}{-(-1+x)}=\frac{1}{x-1}+\frac{-1}{x-1}=\frac{1}{x-1}-\frac{1}{x-1}=0

  • Beachte außerdem, dass du nie aus Summen kürzen darfst!

Beispiel 1: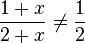 \frac{1+x}{2+x} \not= \frac{1}{2} , Beispiel 2: 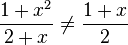\frac{1+x^2}{2+x} \not= \frac{1+x}{2}, Beispiel 3: 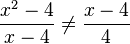\frac{x^2-4}{x-4} \not= \frac{x-4}{4} x darf man nicht kürzen!
Beispiel 4: 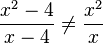\frac{x^2-4}{x-4} \not= \frac{x^2}{x}, Beispiel 5: 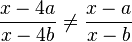\frac{x-4a}{x-4b} \not= \frac{x-a}{x-b} 4 darf man nicht kürzen!


Video2.jpg Kürzen und Erweitern, Bruchterme,
von TheSimpleMaths: Bruchterme vereinfachen, Grundlagen, Tipps und Tricks

Aufgaben:
Du brauchst Stift und Papier und rechnest selbst. Wenn du fertig bist, kannst du deine Lösung vergleichen.

Kürzen
Addition
Multiplikation 

Binomische_Formeln - Binomische Formeln sind oft hilfreich beim Rechnen mit Bruchtermen.

Bruchgleichungen

  • Eine ausführliche Erklärung zu Bruchtermen und Bruchgleichungen mit Umformungen und Rechenbeispielen findest du auf dieser Seite

So löst man Bruchgleichungen

Video2.jpg Bruchgleichungen von TheSimpleMaths, Beispiel, Bruchgleichungen, schwierigere Aufgabe

Aufgaben:
Aufgaben mit Lösungen - Bearbeite die Aufgaben 1 und 2!
weitere Aufgaben mit Lösungen

Von „http://rsg.zum.de/index.php?title=Bruchterme_und_Bruchgleichungen&oldid=7245“