Das Federpendel: Unterschied zwischen den Versionen
| Zeile 5: | Zeile 5: | ||
Wir verstehen unter einem Federpendel einen an einer senkrechten Schraubenfeder befestigten Körper, den man durch Auslenkung aus der Ruhelage in Schwingungen versetzen kann. Desweiteren gehen wir davon aus, dass keine Reibungsverluste auftreten. Man spricht dann von einem ungedämpften Federpendel.<br> | Wir verstehen unter einem Federpendel einen an einer senkrechten Schraubenfeder befestigten Körper, den man durch Auslenkung aus der Ruhelage in Schwingungen versetzen kann. Desweiteren gehen wir davon aus, dass keine Reibungsverluste auftreten. Man spricht dann von einem ungedämpften Federpendel.<br> | ||
| + | |||
| + | {{Aufgaben-blau||2=Nenne bestimmende Größen des Federpendels.}} | ||
| + | |||
| + | {{Lösung versteckt|1=Bestimmende Größe der Feder ist ihre Federkonstante D und bestimmende Größe des Pendelskörpers ist seine Masse m.}} | ||
{{Aufgaben-blau||2=a) Beschreibe die Ausgangslage des Federpendels auf dieser [https://www.walter-fendt.de/html5/phde/springpendulum_de.htm Seite].<br> | {{Aufgaben-blau||2=a) Beschreibe die Ausgangslage des Federpendels auf dieser [https://www.walter-fendt.de/html5/phde/springpendulum_de.htm Seite].<br> | ||
Ist die Ausgangslage auch gleichzeitig Ruhelage?<br> | Ist die Ausgangslage auch gleichzeitig Ruhelage?<br> | ||
| − | b) Starte nun das Applet. Was kannst du über die Zeit-Orts-Funktion aussagen. Gib ihre Funktionsgleichung an.}} | + | b) Starte nun das Applet. Was kannst du über die Zeit-Orts-Funktion aussagen. Gib ihre Funktionsgleichung an.<br> |
| + | c) Ändere im Applet die bestimmenden Größen D und m des Federpendels. Was stellst du fest?<br> | ||
| + | d) Ändere die Amplitude des Federpendels. Was stellst du fest?<br> | ||
| + | e) Du kannst die Simulation auch mit anderer Fallbeschleunigung ausführen, z.B. Fallbeschleunigung auf dem Mond g<sub>Mond</sub>=1,6m/s².}} | ||
{{Lösung versteckt|1=a) In der Ausgangslage ist das Federpendel nach oben aus der Ruhelage ausgelenkt. Lässt man es los, dann bewegt es sich nach unten und kann Schwingungen ausführen.<br> | {{Lösung versteckt|1=a) In der Ausgangslage ist das Federpendel nach oben aus der Ruhelage ausgelenkt. Lässt man es los, dann bewegt es sich nach unten und kann Schwingungen ausführen.<br> | ||
Die Ausgangslage ist nicht gleichzeitig Ruhelage. Fasst man einen Körper in der Ruhelage an und lässt ihn wieder los, so ändert sich nichts er bleibt weiterhin in Ruhe. Dies ist hier in der Ausgangslage nicht der Fall.<br> | Die Ausgangslage ist nicht gleichzeitig Ruhelage. Fasst man einen Körper in der Ruhelage an und lässt ihn wieder los, so ändert sich nichts er bleibt weiterhin in Ruhe. Dies ist hier in der Ausgangslage nicht der Fall.<br> | ||
| − | b) Zur Zeit t = 0s ist das Pendel maximal ausgelenkt. Es ist y(0) = A. Lässt man es los, dann schwingt es nach unten. Der Verlauf ist durch eine Kosinusfuntkion gegeben. <math> y = A cos(\omega t)</math>.} | + | b) Zur Zeit t = 0s ist das Pendel maximal ausgelenkt. Es ist y(0) = A. Lässt man es los, dann schwingt es nach unten. Der Verlauf ist durch eine Kosinusfuntkion gegeben. <math> y = A cos(\omega t)</math>.<br> |
| − | + | c) Bei kleinerer Federkonstante D zieht sich die y(t)-Funktion auseinander,sie wird gedehnt, die Schwingungsdauer T wird größer.<br> | |
| + | Bei größerer Federkonstante D wird die y(t}-Funktion gestaucht, sie zieht sich zusammen, die Schwingungsdauer wird kleiner.<br> | ||
| + | Auch wird die y(t)-Funktion bei größerer Masse m gedehnt, sie zieht sich auseinander, die Schwingungsdauer T wird größer.<br> | ||
| + | Wird die Masse m verringert, dann wird die y(t)-Funktion gestaucht, sie zieht sich zusammen, die Schwingungsdauer T wird kleiner.<br> | ||
| + | d)Die Amplitude der y(t)-Funktion wird entsprechend geändert. | ||
| + | e) Ändert man die Fallbeschleunigung so bleibt die y(t)-Funktion unverändert.}} | ||
Version vom 19. März 2020, 11:41 Uhr
Das Federpendel kennst du nun schon vom Einführungsversuch, als seine Schwingung mit der Projektion einer Kreisbewegung übereinstimmte. Du kennst das Federpendel, aber auch schon aus dem Physikunterricht deiner bisherigen Klassen. In der 7. Klasse hast du das Hookesche Gesetz kennengelernt, welches du in der 8. Klasse für die Spannenergie gebraucht hast.
30px Merke
Ein Federpendel besteht aus einem Pendelkörper, der an einer Schraubenfeder hängt. 50px |
Wir verstehen unter einem Federpendel einen an einer senkrechten Schraubenfeder befestigten Körper, den man durch Auslenkung aus der Ruhelage in Schwingungen versetzen kann. Desweiteren gehen wir davon aus, dass keine Reibungsverluste auftreten. Man spricht dann von einem ungedämpften Federpendel.
a) In der Ausgangslage ist das Federpendel nach oben aus der Ruhelage ausgelenkt. Lässt man es los, dann bewegt es sich nach unten und kann Schwingungen ausführen.
Die Ausgangslage ist nicht gleichzeitig Ruhelage. Fasst man einen Körper in der Ruhelage an und lässt ihn wieder los, so ändert sich nichts er bleibt weiterhin in Ruhe. Dies ist hier in der Ausgangslage nicht der Fall.
b) Zur Zeit t = 0s ist das Pendel maximal ausgelenkt. Es ist y(0) = A. Lässt man es los, dann schwingt es nach unten. Der Verlauf ist durch eine Kosinusfuntkion gegeben. 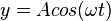 .
.
c) Bei kleinerer Federkonstante D zieht sich die y(t)-Funktion auseinander,sie wird gedehnt, die Schwingungsdauer T wird größer.
Bei größerer Federkonstante D wird die y(t}-Funktion gestaucht, sie zieht sich zusammen, die Schwingungsdauer wird kleiner.
Auch wird die y(t)-Funktion bei größerer Masse m gedehnt, sie zieht sich auseinander, die Schwingungsdauer T wird größer.
Wird die Masse m verringert, dann wird die y(t)-Funktion gestaucht, sie zieht sich zusammen, die Schwingungsdauer T wird kleiner.
d)Die Amplitude der y(t)-Funktion wird entsprechend geändert.
Extras:
Hier ist ein waagrechtes Federpendel beschrieben.

